
目 次
雑科学ホーム
hr-inoueホーム
理論計算及び考察
水素の収着熱は4つの項に分割できる。
qst = -[E(D)] - [E(R)] + [α F2/2] - [Q F'/2]
ここで、E(D) は分散エネルギー、E(R) は反発エネルギー、α F2/2 は誘起双極子と静電場の相互作用エネルギー(α は水素の分極率、F は静電場の大きさ)、また Q F'/2 は四重極子と静電場の勾配の相互作用エネルギー(Q は水素の四重極子能率、F' は静電場の勾配)である。モルデナイトについて図7に示すように座標軸をとり、このY軸上で各エネルギーの値を計算した。なお、ここでの計算では、注目する水素分子を取り巻く63個の単位格子中の全イオンの影響を積算しており、NEC製PC8001マイクロコンピューターを用いて行なった。
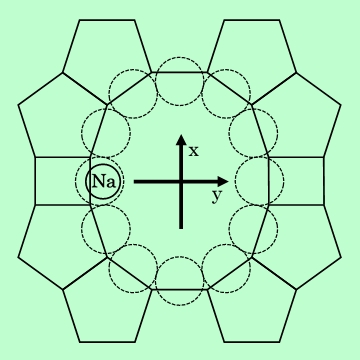
図7 モルデナイト細孔内の座標軸
[E(D)] + [E(R)] の値は次のような式で計算される17),18)。
[E(D)] + [E(R)] = -Σ {μH2-i / ri6}+ Σ {λH2-i / ri12}
ここで、i は格子中の i 番目のイオンを表し、r は注目する収着水素分子からイオンまでの距離である。また μ と λ は定数で、高石らの方法に従って決定した19)。この値のY軸上での変化を図8に示す。このように細孔中でほぼ一定で約1.7kcal/molになっている。
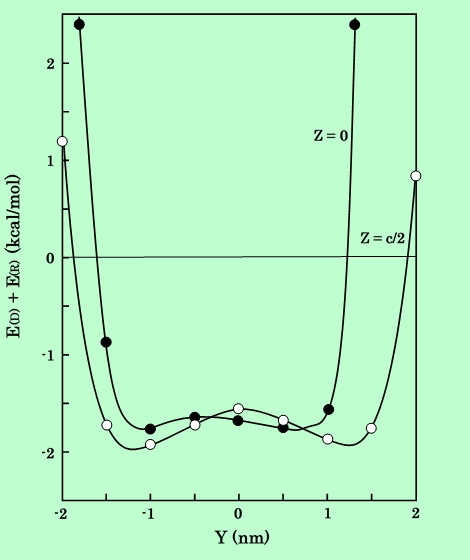
図8 細孔内の分散エネルギーと反発エネルギー
静電場の大きさとその勾配は次の式で求める。
Fτ = Σ d(ei / ri) / dτi = -Σ ei τi / ri3
F'τ = d Fτ / dτ = -Σ ei (ri2 - 3τi2) / ri5
ここで、ei はi番目のイオンの電荷を、また τ は x, y, z を代表するものである。これらの値を図9に示す。Fx と Fz はY軸上でほとんど0であるので、ここでは省略してある。
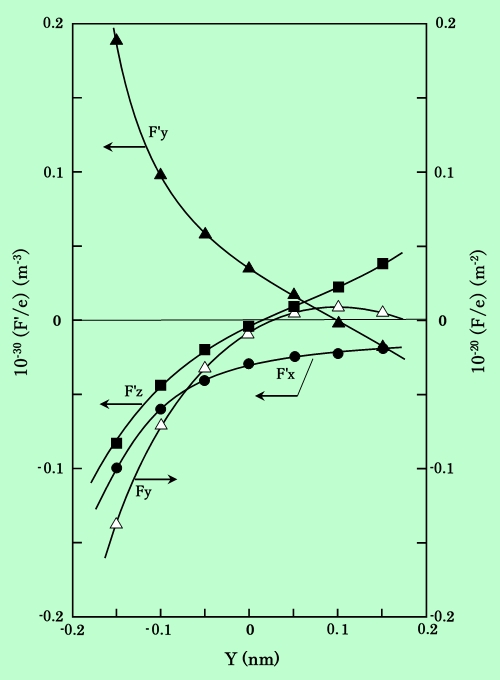
図9 細孔内の静電的エネルギー
ここで注目されるのは F'y の値がプラスになっていることで、これは水素分子がY軸と平行に、即ちナトリウムイオンに対して垂直に配向した場合、四重極子が反発力を受けることを表している。
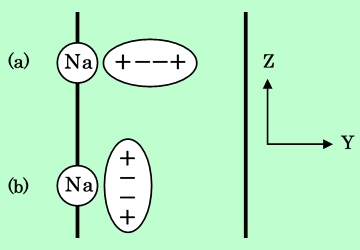
図10 四重極子の吸着モデル
誘起双極子と静電場の相互作用によると水素分子は図10(a)のようにY軸に平行に配向した方が安定になるが、その場合、Y軸に垂直、即ちナトリウムイオンに対して水平に配向した場合とのエネルギー差は0.2kcal/mol程度で、束縛回転の要因としては不充分である。これに対して四重極子と静電場の勾配の相互作用の方は、図10(b)のようにY軸に対して垂直に配向した方が安定となり、反発力の働く水平配向とは数kcal/molの差がある。このことから、水素分子はモルデナイト細孔中でY軸に垂直、ナトリウムイオンに対して水平に配向しており、束縛回転の主な要因は四重極子と静電場の勾配の相互作用であると結論される(表III)。
表III モルデナイト細孔中の水素分子のエネルギー
| Na 電荷 |
+1 |
+0.6 |
| (1) |
-α⊥F2/2 |
-0.87 |
-0.29 |
| (2) |
(QF'/2)⊥ |
-1.51 |
-0.87 |
| (3) |
(1) + (2) |
-2.38 |
-1.16 |
| 空間因子 asf |
1/3 |
2/3 |
| (3) × asf |
-0.79 |
-0.77 |
| (4) |
-α//F2/2 |
-1.14 |
-0.37 |
| (5) |
(QF'/2)// |
3.10 |
1.70 |
| (6) |
(4) + (5) |
1.96 |
1.33 |
| {(6)-(3)}×asf |
1.45 |
1.66 |
⊥,// は、Y軸に対してのもの
モルデナイト中のイオンの電荷の値も考慮して20)、この誘起双極子と静電場、四重極子と静電場の勾配の両相互作用の値の和を求めると、表IIIに示すように1〜2kcal/molという値が出てくる。しかしこれは水素分子が細孔中の一ケ所に留まっている場合のものである。実際にはある程度動いているということがエントロピーの値からも示されているので、この運動により収着熱は多少減少していると考えられる。そこで空間因子というものを定義して、電気的なこれら二つの相互作用の和に、この空間因子をかけたものが実際に収着熱に寄与するものと考える。収着熱の実測値は約2.5kcal/molであり、[E(D)]、[E(R)]の項は前記のように1.7kcal/molであるから、この電気的な相互作用の寄与は0.8kcal/molとなるはずである。この場合の空間因子の値はNaの電荷を+1と考えた場合は1/3、+0.6と考えた場合は2/3であり、動くことによる収着熱の減少はそれぞれ1.6kcal/mol及び0.4kcal/molである。これだけのエネルギーを失っても水素分子が運動するということは、その損失を補うだけのエントロピーの増加があるということである。運動によるエントロピーの増加は表Iに示すように約10cal/mol/Kであるから、これによる自由エネルギーの減少は約0.9kcal/molとなる。従って、収着熱の減少は0.9kcal/mol以下でなければならないので、Naの電荷は+0.6と+1の間で、空間因子は1/3〜2/3という値をとるのが妥当である、という結論が得られる(表III)。
このようにして収着熱の実測値と理論計算との比較から求めた空間因子を用いて、水平配向と垂直配向の実質的なエネルギー差、即ち束縛回転の障壁値を計算すると、1.5kcal/molとなった。このように回転が束縛されると、o-H2が占める回転量子数J=1の3つの縮重準位の内の一つのエネルギーが上昇し、実質的に縮重度は2となる。また、このJ=1のエネルギー準位と、p-H2が占めるJ=0の回転エネルギー準位とのエネルギー差は348calから240calに減少する。これらの数値から分配関数を用いた式で収着分離係数を計算すると、77Kで1.34、90Kで1.24となった。実測値は表Iに示すように77Kで1.40、90Kで1.30であるから、収着熱から見積もった空間因子は妥当な数値であることが、収着分離係数の面からも確認できた。
目 次
雑科学ホーム
hr-inoueホーム




