
目 次
雑科学ホーム
hr-inoueホーム
第4章
粒子間相互作用の計算による磁性粒子の分散・凝集の解析
1. 緒 言
前章までに、磁性粒子分散系に関する種々の実験的な研究結果について述べてきた。これらの研究の中で、様々な条件下での磁性粒子の分散性に関して検討したが、粒子の分散・凝集を定量的に解釈するには、実験的研究だけでなく理論的な裏付けも必要である。
コロイド分散系の分散安定性に関する理論的な研究は古くから数多く行なわれているが、その大部分は非磁性粒子を対象としたものである。非磁性粒子分散系において粒子間に働く相互作用力としては、van der Waals力1)、静電相互作用力、粒子表面に形成された高分子吸着層による立体反発力などがある。このうちvan der Waals力と静電反発力だけが働く系での分散性は、DLVO理論によってほぼ完全に記述されている2),3)。
一方、高分子吸着層による立体反発力に関しても、DLVO理論ほど完成されてはいないが、非常に多くの理論が発表されている4)。Mackorらは、粒子の接近時に吸着層が圧縮されることによるエントロピーの減少が反発力をもたらす、というエントロピー斥力理論を提唱した5),6)。Mackorの理論では吸着分子は剛直な棒状であると仮定されており、実際の高分子に適用するにはやや問題がある。Clayfieldらはこの点を改良し、モンテカルロ法を用いて分子の柔軟性も考慮したエントロピー計算を行なっている7)。これらのエントロピー斥力理論とは別に、Fischerは吸着層が互いに重なり合うモデルを考え、重なり合った領域の浸透圧の増加が反発力を発生するという、浸透圧斥力理論を発表した8)。この理論では、反発力はエンタルピーの効果によって生じており、吸着高分子と溶媒との相互作用も考慮されている。浸透圧斥力理論は、Ottewillらによってさらに発展させられ、温度の効果等が明確にされた9)。これらの2種類の理論に対して、Meierはエントロピーとエンタルピーの両方が反発力に寄与するとして、吸着層内の分子密度分布も考慮に入れた反発エネルギーの表式を導出した10)。この理論には、後にHesselinkらによって修正が加えられている11)。またBagchiは吸着層が圧縮されるモデルと重なり合うモデル(混合モデル)の各々について、エントロピーとエンタルピーの両方の効果を取り入れた理論を展開した12)。圧縮モデルでは、エントロピー効果の他に、吸着層から溶媒が絞り出されることによるエンタルピーの効果も加味されており、また混合モデルでも、吸着層内での高分子濃度の増加に伴うエントロピーとエンタルピーの両方の変化を考慮した式が導かれている。この他に、平行平板間についてではあるが、Gerberらによる変分法を用いた理論13)、Levine14)やScheutjensら15)によるマトリックス法による理論など、より厳密に相互作用エネルギーを求めようとする研究も行なわれている。
立体反発力とは別に、吸着していない高分子によって粒子の凝集が起こるというdepletion凝集の理論も最近では盛んに研究されている16)-18)。また、雲母などの劈開面に限られているが、2面間に働く力を直接測定する、いわゆる Surface Force Apparatusを用いた研究も行われるようになっており19),20)、理論の検証に大きな役割を果たすことが期待されている。
一方、磁性粒子分散系に関しては、磁気的引力と静電反発力、立体反発力を考慮したScholtenによる計算がある21),22)。ここでは粒子の磁化は双極子で近似されており、また磁性流体を念頭に置いているため、数十nm程度の微細な球形粒子が対象となっている。尾崎らはヘマタイト粒子について、磁気的引力と静電反発力とを考慮して粒子間ポテンシャルを求めている23),24)。しかし本来ヘマタイトは反強磁性物質であり、寄生強磁性に基づくごく弱い磁化しか持たないので、いわゆる強磁性粒子と比べると相互作用力が4桁以上小さい。またChanらは、表面被覆層を持つ球形の強磁性粒子に関して、粒子の回転も考慮してポテンシャル計算を行なった25)。この計算においては表面被覆層は剛体が仮定されており、いわゆる立体反発力を発生するような吸着層ではない。
以上のように、非磁性粒子に対して行なわれている詳細な解析が、現実的な強磁性粒子分散系に適用された例はほとんどない。そこで本章では、前章までに検討してきた針状および板状粒子分散系に対して、Bagchiの理論を応用した解析を試みる。Bagchiの理論には、吸着層内での高分子の一様な分布が仮定されているなど、厳密には問題点もある。しかし比較的単純で明快な形式を持っており、また計算に必要なパラメーターのほとんどがこれまでの研究で実測できているので、本研究の系で立体反発力を求めるのに非常に都合がよい。この立体反発力にvan der Waals引力と磁気的引力とを加えて、種々の条件下での粒子間ポテンシャルを計算し、磁性粒子の分散・凝集の現象を解析する。また磁気的引力に関しては、単純な双極子モデルや、より厳密なモデルなどの比較、検討も行なう26),27)。
2. 双極子モデルによる粒子間ポテンシャルの計算
溶媒中に分散した磁性粒子間に働く相互作用力としては、磁気的相互作用、静電的相互作用、van der Waals相互作用、表面吸着層の立体反発相互作用などがある。本研究で扱っている分散系では磁性粒子のζ電位はゼロであったので、このうちの静電的相互作用は考慮しなくてもよい。そこで、2個の粒子間に働く他の3つの相互作用について検討して行くことにする。磁性粒子の磁化を粒子の中心に置いた双極子で近似し、粒子形は高さ方向が磁化容易軸になる円柱(または円板)とする。形状比(磁化容易軸/磁化困難軸)が6の針状粒子と、形状比0.2の板状粒子について、Fig.1に示す2種類の配置での相互作用エネルギーを計算する。
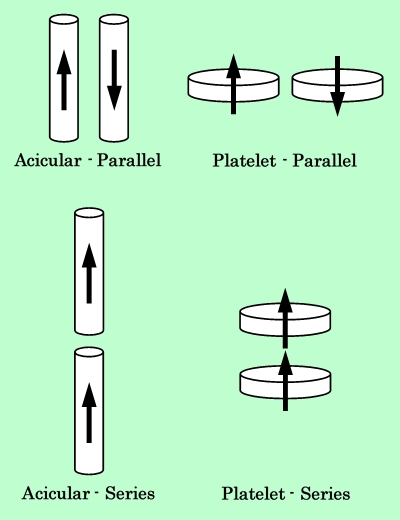
Fig.1 Alignments of magnetic particles for interaction energy calculation.
2.1 磁気的エネルギー
2個の磁気モーメント間の磁気的エネルギー、Vmagは次の式で求められる。
Vmag = - ([M1][M2]/R3)×{3(M1/[M1]・R/[R])(M2/[M2]・R/[R]) - M1/[M1]・M2/[M2]} (4.1)
ここでM1、M2、は磁気モーメント、R は2個の磁気モーメントを結ぶ位置ベクトルである。従って、Parallel配置、Series配置ではそれぞれ次のようになる。
Parallel ・・・・・ Vmag = - M 2/(d + 2r )3 (4.2)
Series ・・・・・・ Vmag = - 2M 2/(d + l )3 (4.3)
ここで、d は粒子表面間距離、r は粒子底面の半径、l は磁化容易軸方向の粒子長である。
2.2 立体反発エネルギー
粒子表面に形成された樹脂吸着層による立体反発エネルギーは、Bagchiの混合機構の理論を用いて計算する12)。この理論では、2個の粒子が接近する際にそれぞれの表面に形成された樹脂吸着層が重なり、その結果、重なった部分の樹脂濃度が増加することによって反発力が生じると考える。Bagchiは球形粒子について計算しているが、ここではBagchiの式を円柱形粒子に適用できるように変形して使用する。Bagchiの式は次のようにして導かれる。
2個の円柱形粒子が接近すると、それぞれの樹脂吸着層が互いに重なり合うようになる。Fig.2にはこの様子が、Parallel配置した針状粒子の場合について示してある。
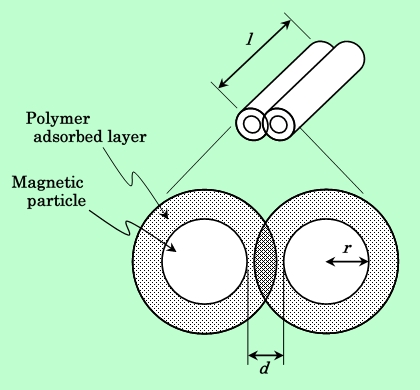
Fig.2 Schematic model of steric repulsion between two particles
with polymer adsorbed layer.
吸着層が重なり合う前の、吸着層中の溶媒のモル濃度をm1、樹脂のモル濃度をm2、また樹脂1分子中のセグメント数をn とすると、吸着層中の溶媒および樹脂の体積分率φ1、φ2は、
φ1 = m1/(m1 + n m2) (4.4)
φ2 = n m2/(m1 + n m2) (4.5)
となる。Flory-Hugginsの理論28),29)によれば、単位体積の上記のような樹脂溶液を作るのに要する自由エネルギー、ΔGは、
ΔG/kT = N0(m1ln φ1 + m2ln φ2 + χ n m2 φ1) (4.6)
と表される。ここで k はボルツマン定数、T は絶対温度、N0はアボガドロ数、χ は溶媒と樹脂の相互作用係数で、右辺の第1項および第2項は混合のエントロピーに関する項、第3項はエントロピーとエンタルピーの両方を含む項である。
吸着層が重なると、樹脂が脱離しなければ樹脂濃度は2倍になり、溶媒はその分だけ追い出される。その結果、溶媒と樹脂の体積分率φ1f、φ2fは次のようになる。
φ1f = (m1 - n m2 )/(m1 - n m2 + 2 n m2) (4.7)
φ2f = 2 n m2 /(m1 - n m2 + 2 n m2) (4.8)
また重なった後の、単位体積当たりの自由エネルギー、ΔGfは、
ΔGf/kT = N0 {(m1 - n m2) ln φ1f+ 2 m2 ln φ2f + 2 χ n m2 φ1f } (4.9)
となる。 従って、吸着層が重なっている部分の体積を vd とすると、吸着層が重なる前後の自由エネルギー変化、即ち立体反発エネルギー、Vst は次のようになる。
Vst = vd (ΔGf - 2ΔG)
= vd N0 kT {(m1 - n m2) ln (φ1 - φ2) - 2 m1 ln φ1 + 2 m2 ln 2 - 2 χ φ22(m1 + n m2)} (4.10)
またvdは、円柱形粒子の場合、次の式で計算できる。
Parallel ・・・・ vd = 2l [(r + L)2cos-1{(r + d /2)/(r + L)} - (r + d /2){(r + L )2 - (r + d /2)2}1/2] (4.11)
Series ・・・・・ vd = π (r + L)2 (2L - d ) (4.12)
ここで、L は樹脂吸着層の厚さで、また角度の単位はラジアンである。
粒子表面間距離 d が樹脂吸着層の膜厚 L よりも小さくなると、単に吸着層どうしが重なるだけでなく、一方の粒子の表面が他方の粒子の吸着層に食い込むようになる。こうなると、重なり合った部分の体積は上の式が示すよりも小さくなるため、反発エネルギーは一層大きくなる。しかし、後に計算結果を示すように、この領域では反発力は他の引力に比べて既に充分に大きくなっており、厳密な値を求めてもあまり意味はないと考えられるので、ここでは上記の式のみで計算することにする。
2.3 van der Waals エネルギー
van der Waalsエネルギーは、Parallel配置の場合、粒子を同じ体積の角柱で近似して、次の平板間の式によって計算する30)。
VvdW = - (A /12π){ 1 / d 2 + 1 / (d + 2r π 1/2)2 - 2 / (d + r π 1/2)2} r l π 1/2 (4.13)
また、Series配置では次の式を用いる。
VvdW = - (A /12π){ 1 / d 2 + 1 / (d + 2l )2 - 2 / (d + l )2}π r 2 (4.14)
ここで、A はHamaker定数である。これらの計算では、樹脂吸着層の寄与は考慮していない。なぜなら、樹脂吸着層は一種の樹脂溶液であり、やや濃度は高いものの分散媒と同種のものであるから(第2章参照)、吸着層が分散液の中でvan der Waals力に特に大きな寄与をするとは考えにくいからである。
2.4 全相互作用エネルギー
以上のようにして求めた3種のエネルギーの総和をとれば、全相互作用エネルギーを求めることができる。即ち、
Vtotal = Vmag + Vst + VvdW (4.15)
となる。なお3種のエネルギー値のうち Vst だけが温度の関数であるため、他の2つに関しても、温度を25℃に固定して kT 単位で表すことにする。
2.5 計算に用いるパラメーター
上記の計算式に現れる各種パラメーターの大部分は既知である。以下にそれらの値を整理しておく。
樹脂吸着層に関するパラメーターは、ほとんど第2章で求められている。吸着層中の樹脂の体積分率、φ2は、溶媒と樹脂の密度が同じであると仮定すると、溶媒がシクロヘキサノンの場合は0.2である。従って、φ1は0.8となる。各成分のモル濃度は、これらの値を分子量で割れば得られる。また樹脂分子中のセグメント数は、通常、溶媒1分子の大きさを単位セグメントと考えて、樹脂と溶媒の分子量の比として与えられる。ただしエポキシ樹脂の場合、分子が屈曲する位置は何箇所か考えられ、溶媒分子の大きさをそのまま単位セグメントとするのはやや難がある。そこで便宜上、ベンゼン環に酸素が1個ついたもの(分子量93:シクロヘキサノン分子に近い大きさ)を単位と考えることにする。樹脂吸着層の厚さは任意に選べるが、標準的な値として5nmに設定した。この値は、第2章で検討したように充分現実的な値である。van der Waalsエネルギーを求めるのに必要なHamaker定数は、α-酸化鉄に対して求められている値、4.5×10-20Jを用いた31)。
必要なパラメーターのうち、相互作用係数、χ だけは適当な値が得られていない。χ は理論的には次のような形で与えられる30)。
χ = u11 + u22 - 2u12 (4.16)
ここで、u11 は溶媒分子間、u22 は樹脂分子間、u12 は溶媒分子と樹脂分子の間の相互作用エネルギーである。χ が負のときは溶解は発熱、即ち、樹脂は溶媒中に自然に溶解する。一方χ が正のときは、樹脂を溶解させるのに何等かのエネルギーが必要である。現実には、χ がかなり大きな正の値(≦0.55)であっても溶解が起こることが知られている30)。本研究の系に関して考えてみると、エポキシ樹脂は溶媒中に簡単には溶解せず、また、30%以上の高濃度では、一度溶解しても数カ月放置するとグリース状の相分離状態になることがある。このようなことから判断して、χ が負になることはあり得ず、おそらくθ 溶媒の条件(樹脂分子の末端間距離がガウス分布になるような条件)に近い、0.5付近であろうと思われる。そこでχ の値が0.2から0.7の範囲で立体反発エネルギーを計算し、その影響を調べてみた。Fig.3にその結果を示す。
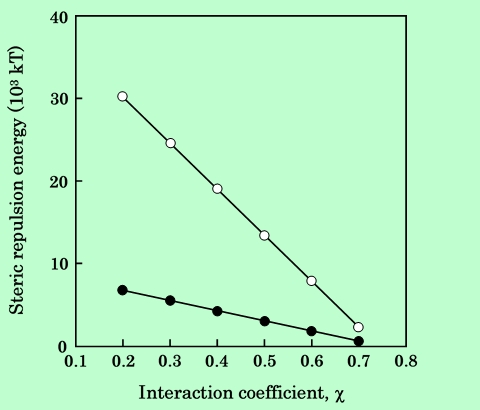
Fig.3 Effect of interaction coefficient between resin and solvent
on steric repulsion energy. Magnetic particles used are acicular
one (black circles) and platelet one (white circles).
粒子配置は、針状粒子がParallel、板状粒子がSeriesである。この図からわかるように、χ が0.4の場合と0.6の場合で約2倍の違いであり、オーダーが変わるほどではない。従って、χ の値を0.5に設定しておけば、計算値にはそれほど大きな誤差は生じないであろう。
Table1に、計算に用いる各パラメーターの標準値をまとめておく。以下の計算では、ここに示した条件を標準として、各パラメーターを適宜変えながら検討して行く。
Table 1 Parameters used for calculation.
| |
Parameter |
Value |
| Particle |
Magnetization, M |
75 emu/g |
| Acicular particle size |
| long axis, l |
300 nm |
| short axis size, 2r |
2×25 nm |
| Platelet particle size |
| Thickness, l |
31 nm |
| Radius, r |
78 nm |
Resin
adsorbed
Layer |
Thickness, L |
5 nm |
| Molecular weight |
2900 |
| Resin volume fraction, φ |
0.2 |
| Number of segment, n |
31 |
| |
Solvent |
Cyclohexanone |
| Interaction coefficient, χ |
0.5 |
2.6 計算結果
まず初めに、Fig.1に示した4種類のケースについて粒子間ポテンシャルを計算した。結果をFig.4に示す。
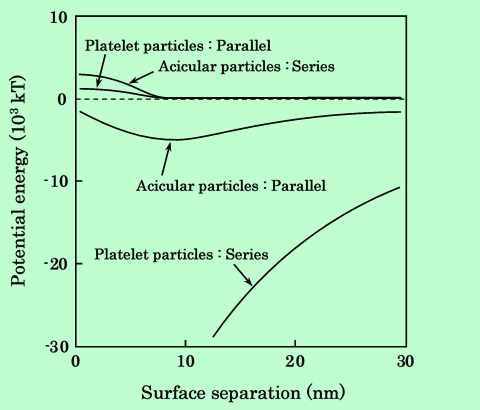
Fig.4 Potential curves calculated with dipole model for various alignments
of magnetic particles.
ポテンシャル曲線には、ごく近距離に大きな引力エネルギー、やや離れたところに反発の極大、その外側に2次極小が現れており、DLVO理論などで見られる形によく似ている。(この図では表面間距離1nm以下は表示していないので1次の極小値は現れていない。)しかし、エネルギーの絶対値は103〜104kTにもなり、DLVO理論で扱う非磁性粒子と比べて非常に大きな値になっている。粒子配置を比較すると、針状粒子に関してはParallel配置の方が2次極小が深く、板状粒子では逆にSeries配置の方が深いことがわかる。特にSeries配置の板状粒子では極端に引力が強く、このモデルで計算する限り非常に凝集しやすいことになる。
次に、Parallel配置の針状粒子について、粒子サイズの影響を検討してみた。粒子の形状比はいずれも6である。計算結果をFig.5に示す。
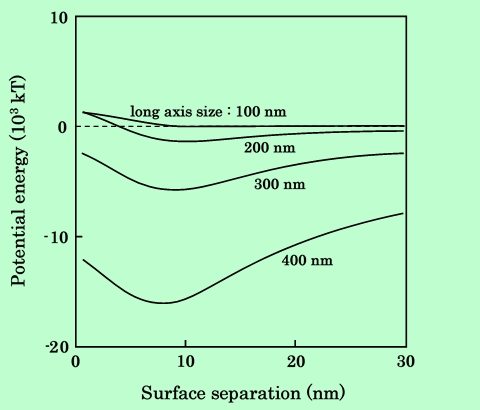
Fig.5 Potential curves calculated with dipole model for various sizes
of acicular magnetic particles.
粒子が大きくなると、吸着層の重なり体積が大きくなるので反発力は増加するが、それ以上に磁気的引力が増大し、2次極小は非常に深くなることがわかる。微細粒子は分散させることが難しいと言われるが、2次極小が浅いことから、一度分散させてしまえば再凝集は起こりにくいといえる。
3. 計算方法の改良
3.1 セル分割モデルの概要
前節では磁気的引力の計算に双極子近似を用いたが、この方法では値の正確さに問題が残る。特に粒子間距離が小さくなった場合、粒子の中心にすべての磁気モーメントが集中したモデルでは、実際からのずれが大きくなってくる24)。そこで、計算をより正確に行なうために、粒子を多数のセルに分割したモデルを検討することにした。分割の方法をFig.6に示す。
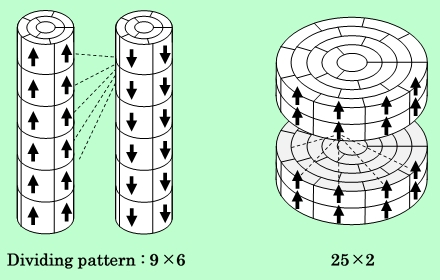
Fig.6 Acicular and platelet magnetic particles divided into cells for calculation
of magnetic interaction. Arrows indicate dipole moment of each cell.
まず粒子をいくつかの同心円筒に分ける。円筒の厚さはすべて同じで、中心の円柱の半径も他の円筒の厚さと同じにする。次に、それぞれの円筒を幾つかのセクターに分割する。分割数は、中心の円柱から数えてn番目の円筒の場合、2n-1である。そして最後に、粒子を磁化容易軸に垂直な面で切り分ける。このようにすると、分割された各セルの体積はすべて同じになる。分割の仕方は、Fig.6の中にも示しているように、(底面の分割数)×(磁化容易軸方向の分割数)で表すことにする。
各セルの中心に同じ大きさの磁気モーメントを配置し、次の式によって、異なる粒子に属するセル間の相互作用をすべて積算すれば磁気的相互作用が求められる。
Vmag = - Σ [([μi][μj]/[R]3)×{3(μi/[μi]・R/[R])(μj/[μj]・R/[R]) -μi/[μi]・μj/[μj]}] (4.17)
ここで、μ は各セルの磁気モーメント、R は磁気モーメントを結ぶ位置ベクトルである。従って、ParallelおよびSeries配置の場合は次のようになる。
Parallel ・・・・・ Vmag = -Σ (μ2/R3)(-3cos2θ + 1) (4.18)
Series ・・・・・・ Vmag = -Σ (μ2/R3)(3cos2θ - 1) (4.19)
ここでθ はμ とR のなす角である。
3.2 セル分割条件の検討
セル分割数が多いほど計算の精度は上がるが、計算量は急激に増大する。そこで、どの程度の分割数にすれば充分な精度が得られるかを検討した。Fig.7〜12にその結果を示す。セル数1×1というのは分割なし、即ち双極子モデルによる計算結果を表している。
Fig.7、Fig.8は針状粒子の場合である。セル数1×1の場合のみ傾向が大きく外れており、双極子モデルではParallel配置のときに磁気的引力を過大評価、Series配置のときは逆に過小評価していることがわかる。またセル数が1×6になると、既にかなり高い計算精度が得られていると言える。Fig.9は磁気的エネルギーをセル分割数の関数として表したものであるが、この図から判断して、分割数が10を越えればほとんど計算精度に問題はなさそうである。ただし粒子表面間距離dが1nm程度になると分割数の影響がやや大きくなっているので、100以上の分割数にした方が無難であろう。
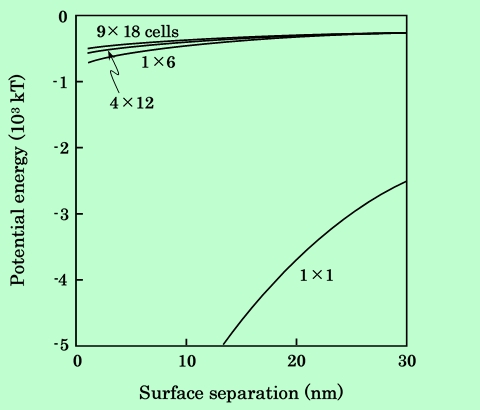
Fig.7 Effect of number of cells on calculated potential energy between
parallel aligned acicular particles.
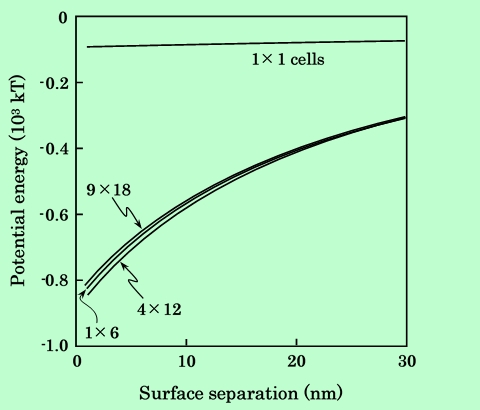
Fig.8 Effect of number of cells on calculated potential energy between
series aligned acicular particles.
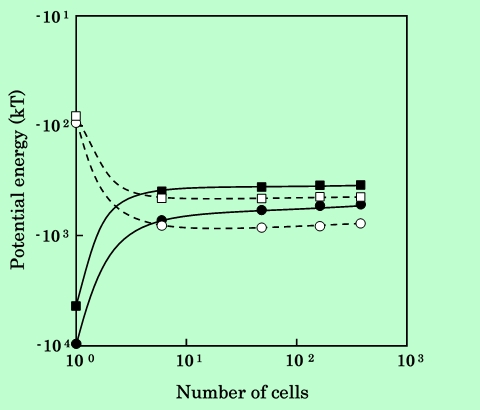
Fig.9 Dependence of calculated potential energy between acicular particles
on number of cells.
black circles : parellel aligned particles at surface separation of 1 nm.
black squares : parellel aligned particles at surface separation of 16 nm.
white circles : series aligned particles at surface separation of 1 nm.
white squares : series aligned particles at surface separation of 16 nm.
同様にして板状粒子について検討したのが Fig.10〜12である。板状粒子の場合は、針状粒子よりも分割数を多くしなければ同等の精度は得られないことがわかる。また双極子モデルによる計算では、針状粒子の場合とは逆にParallel配置で磁気的エネルギーが過小評価、Series配置で過大評価になっていることが示されている。
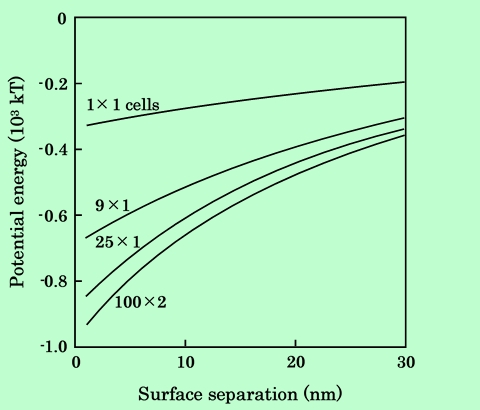
Fig.10 Effect of number of cells on calculated potential energy between
parallel aligned platelet particles.
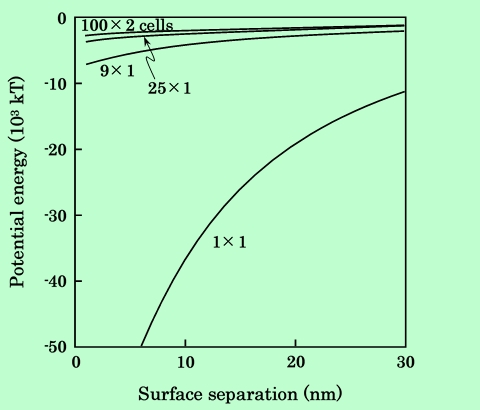
Fig.11 Effect of number of cells on calculated potential energy between
series aligned platelet particles.
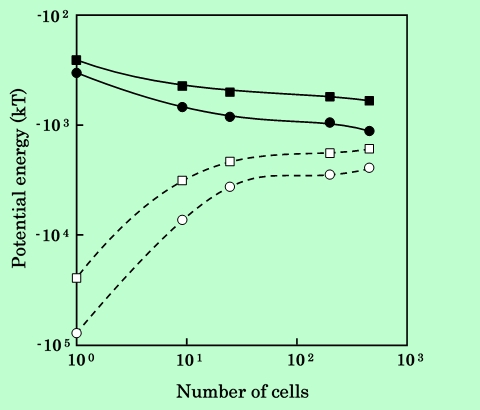
Fig.12 Dependence of calculated potential energy between platelet particles
on number of cells.
black circles : parellel aligned particles at surface separation of 1 nm.
black squares : parellel aligned particles at surface separation of 16 nm.
white circles : series aligned particles at surface separation of 1 nm.
white squares : series aligned particles at surface separation of 16 nm.
以上の結果を基に、セル分割モデルによって磁気的エネルギーの計算する際の分割数は、針状粒子で9×18 = 162、板状粒子で100×2 = 200に設定した。
3.3 計算モデルの比較
磁気的エネルギーを計算するには、これまで検討してきた双極子モデル、セル分割モデルの他に、粒子の両端にN、Sの単磁極を置くモデル(単磁極モデルと呼ぶことにする)を用いることもできる。このモデルによる計算式は次のようになる。
Parallel ・・・・・ Vmag = - 2 p 2 / (d + 2r) + 2 p 2 / {(d + 2r)2 + l 2 }1/2 (4.20)
Series ・・・・・・ Vmag = - p 2 / d - p 2 / (d + 2l ) + 2 p 2 / (d + l ) (4.21)
ここで、p は単磁極の大きさで、p = M /l で与えられる。単磁極モデルも含めた3種の計算方法を比較した結果を Fig.13〜16に示す。
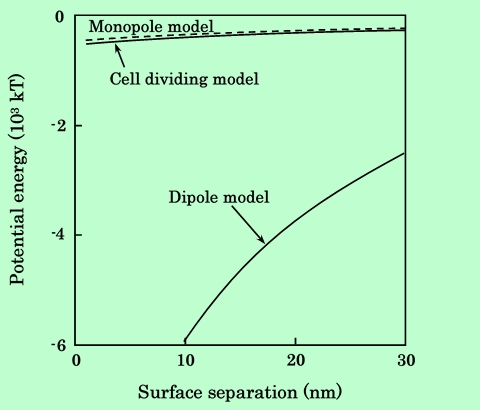
Fig.13 Comparison of calculation methods for parallel aligned acicular particles.
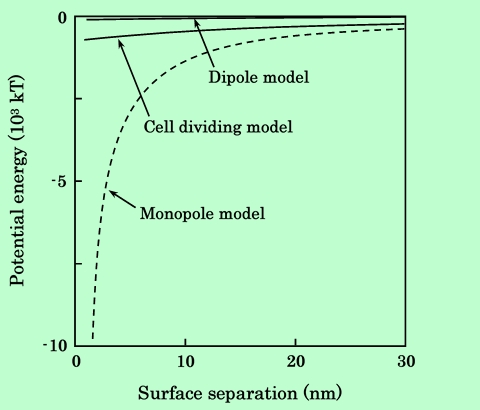
Fig.14 Comparison of calculation methods for series aligned acicular particles.
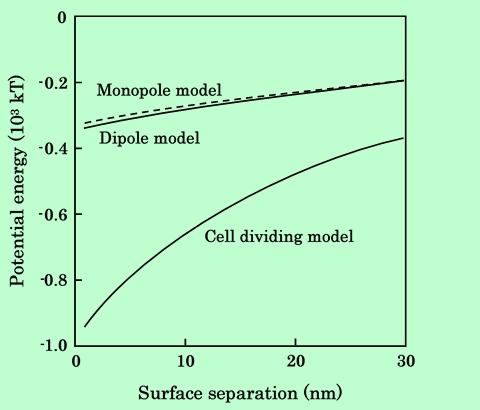
Fig.15 Comparison of calculation methods for parallel aligned platelet particles.
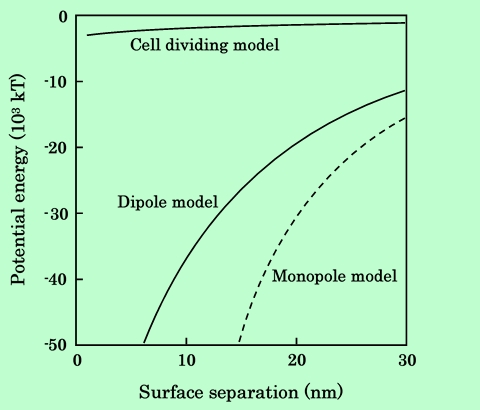
Fig.16 Comparison of calculation methods for series aligned platelet particles.
単磁極モデルは、Parallel配置の針状粒子に対してはセル分割モデルに非常に近い値を与えるが、その他の場合はむしろ双極子モデルよりも差が大きくなっている。従って正確な計算を行なうためには、やはりセル分割モデルを用いることが必要である。
3.4 van der Waals エネルギー計算方法の改良
前節のvan der Waalsエネルギーの計算では、粒子を角柱で近似して、平板間のエネルギーを計算する式を適用したが、これも近似としてはやや粗いものである。正確に求めるためには、磁気的エネルギーと同様にセル分割で計算するか、または全体積にわたって積分するかのどちらかの方法によらなければならない。しかし、磁気的エネルギーに比べてvan der Waalsエネルギーの寄与は小さいので、それほどの精度は要求されないであろう。そこで、粒子を同じ厚さの5層に分割して、各層間の相互作用エネルギーを積算する方法を採ることにした。分割方法をFig.17に示す。
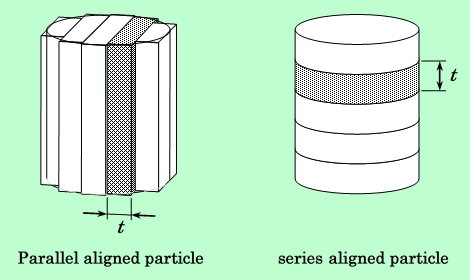
Fig.17 Cell dividing method for calculation of van der Waals energy.
分割面はもう一方の粒子のある方向に対して垂直である。即ち、Parallel配置では磁化容易軸に平行な面で円柱(または円板)を縦に割るような形になり、Series配置では磁化容易軸に垂直な面で層状に分割する形になる。Series配置の場合は、分割された部分はすべて、底面積が元の粒子に等しい同型同大の円柱(円板)であるから、平板間の相互作用を求める式がそのまま適用できる。一方Prallel配置の場合は、いろいろな形状、大きさの部分に分割されることになるので、そのままでは扱いにくい。そこで、各部分を図のような角板に置き換えた上で、平板間の式を適用することにする。計算式は次のようになる。
VvdW = - Σ (A /12π){ 1 / di2 + 1 / (di + 2t)2 - 2 / (di + t)2} S (4.22)
ここで、di は相互作用する2つの層の表面間距離、t は層の厚さ、S は対峙する面の平均面積である。

Next
目 次
雑科学ホーム
hr-inoueホーム

















