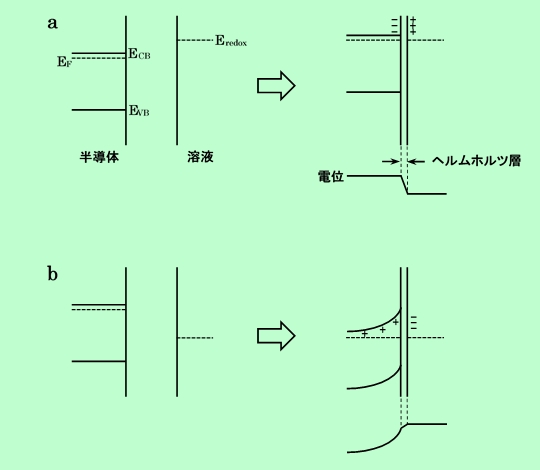
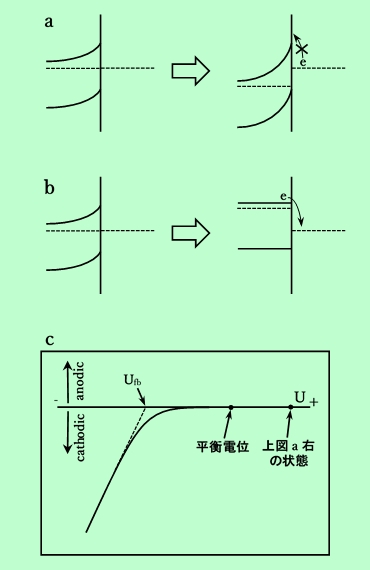
ショットキー障壁が存在する場合には、半導体/溶液界面は整流作用を示す。その様子を図Bに示してある。半導体に正の電荷をかけても、溶液中の電子は伝導帯に入れず、また正孔も存在しないので価電子帯にも入れない。即ち、電流は全く流れない。しかし、負の電位をかけていくとショットキー障壁がしだいに低くなり、バンドが水平になったところで、カソード電流が急激に立ち上がることになる。この時の電位をフラットバンド電位、Ufbと呼ぶ。図B-cに、電流-電位曲線を示しておく。このような曲線を描くことによって、Ufbを求めることができる。
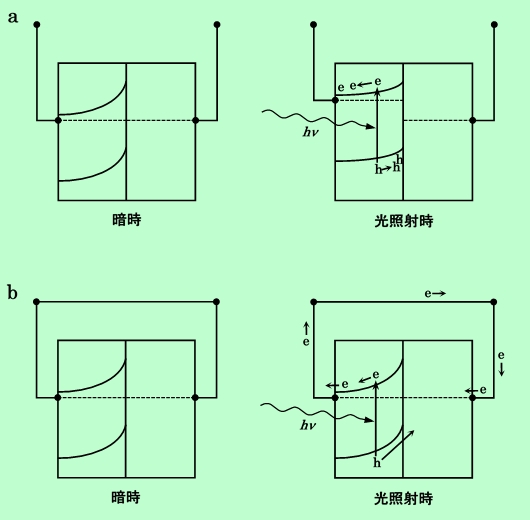
一方、同じ溶液中、或いは電気的に連絡のある別の溶液中に浸した他の電極と半導体とを外部回路で短絡した場合、分離した電子-正孔対は半導体から出て行く、即ち電子は外部回路を通って対極へ移り、そこから溶液中へ入り、正孔は界面を通して液中へ入るか、或いは半導体表面を酸化して消失する。このようにして光生成した電子、正孔は、電流として回路を流れることになり、半導体内部には蓄積されないので、半導体のバンドの状態は元のままである。即ち、両極間に電位差はない。この状態で得られる光電流を短絡電流、ISH と呼び、これは生成可能な最大の電流である(図C-b)。
外部回路に抵抗を挿入すると、電流がその抵抗値に応じて抑えられるため、半導体内に電子、正孔が蓄積され、電位差が生じるようになる。そこで、外部回路の抵抗を変えながら両極間の電圧と電流を測定して行くと、図D-aのような光電流-光電圧曲線を描くことができる。
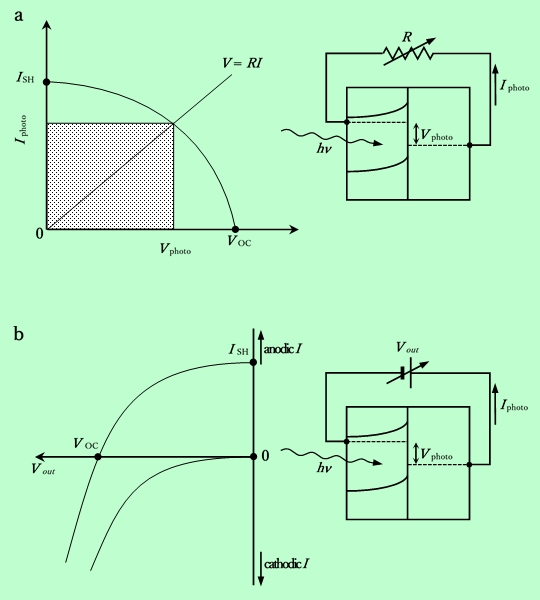
図D 光電流-光電圧 曲線
a. 外部抵抗を利用した場合、 b. 外部起電力を利用した場合
出力は光電流と光電圧の積で与えられるから、図中の斜線の部分の面積で表される。従ってこの部分の面積が最大になるような位置が存在し、その時の外部抵抗の値も決定できる。その点の電流、電圧を Imax、Vmax とすると、最大出力 Wmax = Vmax × Imax は、曲線の形が長方形の二辺に沿った形になるほど大きくなり、その程度を表す値として、f.f. = Wmax / (VOC × ISH) を定義することができる。この値はフィルファクターと呼ばれ、半導体/溶液界面を利用した光電気化学セルに於いては比較的大きいもので0.5〜0.6という値が得られている。
一般には、電流-電圧曲線を測定するには、上述のような外部抵抗を変えるという方法はあまり行なわれず、外部回路中に光電圧と逆の方向の起電力を挿入する、という方法が採られる。つまり、I-U 曲線と同じ要領で、横軸に電位ではなく電圧をとるわけである。この曲線の暗時と光照射時との対比を図D-bに示してある(実際にはこのような平行移動にならない場合も多い)。光照射時の曲線の縦軸切片は図D-aと同じ短絡状態であり、ISH を表す。一方、横軸切片はバンドの曲がりがなくなった状態であるから、開放状態と全く同じであり、これが VOC を表すことになる。
一般に、半導体の表面には結晶構造の乱れや、欠陥、結合の切れた部分等が存在し、バルクとは異なるエネルギー状態にある。これらの中にはドナーやアクセプターとして働くものがあり、そのために、これまで述べてきた理想的なモデルでは説明できないような現象を示すことがある。以下に、このような表面準位が存在する場合について述べる。
n型半導体のバンドギャップ中に表面準位が存在すると、その表面準位も一種のフェルミレベルを持っていると考えられるので、バルクのフェルミレベルとの差をなくすために、バルクから表面準位に電子が移動する。その結果、半導体/溶液界面で生じたのと同じような空間電荷層を生じ、空気中でもバンドの曲がりを引き起こす。この状態を、フェルミレベルが表面準位の位置に固定される、という意味で、Fermi Level Pinning と呼ぶ。このようになっている半導体を溶液中に浸した場合のバンドモデルを図Eに示してある。
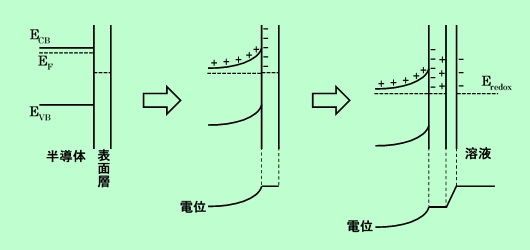
図E 表面準位が存在する場合の半導体と溶液の接触
図ではヘルムホルツ層部分を大幅に広げて描いている。表面準位がない場合は、既に述べたように、半導体中の正電荷はかなり深くまで分布する。これに対して、表面準位が多量に存在する場合には、溶液との電子のやり取りはほとんど表面準位が行なうので、空間電荷層に新たに電荷が導入されることはなく、バンドの曲がりには変化を生じない。溶液から注入された正電荷はすべて表面準位のところにあり、これで溶液中の負電荷を遮蔽してしまうのである。従って半導体の EF と溶液の Eredox との接触前の差は、ヘルムホルツ層中の電位降下で完全に補償されることになる。このような状況は、Eredox が EF よりも負の値になっても変わらず、本来はオーミックな接触になるような場合でも、一定のバンドの曲がりが保持される。その様子を図Fに示す。

図F 種々のEredoxを持つ溶液と半導体との接触
上段:表面準位なし、 下段:表面準位あり
この図から明らかなように、理想的な界面のモデルでは Ufb は Eredox によらず一定で、VOC は Eredox に比例して変化する(ただし、Eredox < EF ではオーミックであるから、VOC は 0)。一方、Fermi Level Pinning の状態では、逆に Ufb が Eredox に比例して変化し、VOC は一定になる。これは、半導体表面に金属を付けて、半導体/金属界面でショットキー障壁を生じさせ、これを溶液中に浸した場合とほとんど同じ状況である。しかし、表面準位が少ない時には、Fermi Level Pinning は不完全で、Eredox の変化の影響は空間電荷層にも部分的に及び、Ufb も VOC も、両極端のモデルの中間の挙動を示すことになる。
この Fermi Level Pinning を定量的に扱うことも試みられている11)。空間電荷層と表面準位を、並列につながった二つのコンデンサーと見なし、その容量に応じて半導体に注入された電荷が分配される、と考える。それぞれの容量をドナー密度や表面準位密度から見積もり、表面準位に蓄えられる電荷が空間電荷層に蓄えられる電荷よりも大きくなれば、Fermi Level Pinning の現象が現れ始めるのである。計算の詳細は省略するが、表面準位密度が 1012cm-2 程度になると Fermi Level Pinning が起こる、ということが示される。表面の原子数は約 1015cm-2 であるから、表面原子の0.1%程度の表面準位が存在すると問題になり始め、1%になると、ほぼ完全なFermi Level Pinning の状態が現れることになる。ただし、実際のコンデンサーの場合は、電圧を上げれば(理想的には)いくらでも電荷を蓄えることができるのであるが、表面準位では数に限りがあるため、それができない。従って、溶液の Eredox の値によっては、一定の容量を持つコンデンサーでは近似できないこともあり得る。つまり、上の計算には全く加味されていない Eredox の影響も実際問題として起こってくるであろう。
参考文献
1)坪村 宏, "光電気化学とエネルギー変換", 東京化学同人 (1980)
2)田村英雄, 松田好晴, "現代電気化学", 培風館 (1977)
3)長 哲郎 編, "電極反応の基礎(共立化学ライブラリー(5))", 共立出版 (1973)
4)前田正雄, "電極の化学", 技報堂 (1961)
5)藤嶋 昭, "化学総説 No.39、無機光化学", 日本化学会 編, p.97, 学会出版センター (1983)
6)高木克己, 山田祥二, "半導体光物性(電子科学シリーズ(8))", 産報出版 (1965)
7)犬石嘉雄, 濱川圭弘, 白藤純嗣, "半導体物性 I, II(基礎物理科学シリーズ 9)", 朝倉書店 (1977)
8)橋口隆吉, 近角聰信, "薄膜・表面現象(材料科学講座 6)", 朝倉書店 (1969)
9)C.Kittel, "固体物理学入門 上・下", 宇野良清, 津屋 昇, 森田 章, 山下次郎 共訳, 丸善 (1974)
10)H.M.Rosenberg, "固体の物理 上・下(オックスフォード物理学シリーズ 9)", 山下次郎, 福地 充 共訳, 丸善 (1977)
11)A.J.Bard, A.B.Bocarsly, F.F.Fan, E.G.Walton, M.S.Wrighton, J. Am. Chem. Soc., 102, 3671 (1980)
目 次
雑科学ホーム
hr-inoueホーム