
目 次
雑科学ホーム
hr-inoueホーム
第3章
磁性粒子分散系の粘度特性
1. 緒 言
コロイド分散系において、分散性を評価する重要な着眼点の一つが粘度特性である。定性的には粘度が高いほど粒子の分散性がよいと判断されるが1),2)、実際には分散系のレオロジーは非常に複雑で、単純には解釈できないのが普通である3-5)。特に磁性粒子においては、磁気的相互作用が働くために流動現象はさらに複雑になり、解析はより困難になることが予測される6)。
非磁性粒子分散系のレオロジーに関しては、古くから多くの研究が行なわれている。流動曲線、即ち剪断速度と剪断応力の関係を表す式としては、降伏値を考慮したBinghamの式7)やCassonの式8)がよく知られているが、これらにさらに修正を加えた多くの表式が発表されている9),10)。また粘度と粒子濃度の関係を表す粘度式としては、相互作用のない球形粒子に関するEinsteinの式11)が最も基本的なものであるが、この他に粒子間相互作用や粒子の形態も考慮に入れるなど、様々な複雑なモデルや式が提唱されている3),12)。これらの粘度式のいくつかはRutgersによって分類、整理されている13)。
一方磁性粒子分散系のレオロジーに関する研究は、Voetらによる、鉄粉/アマニ油系の研究に始まる14)。それ以降の研究では、概して非磁性粒子と同様にCassonの式やMooneyの式15)に基づいて解析したものが多い1),16),17)。その他に、流動曲線をNewton流動の部分と降伏値の部分、凝集構造の弾性変形による部分に分けて解析したKuinの研究18)や、粘度の経時変化から分散液中の構造形成、破壊の過程を追跡した渡辺の研究19)、磁気粘性効果に関する尾崎らの研究20)などがある。また増子らは、分散液の粘度を粒子の体積分率と関係付けて解析した例を報告している21)。
これらの研究も含めて、一般に磁性粒子分散系の研究においては、磁気的引力による凝集を防いで粒子を安定に分散させるために分散剤を添加することが必要になる22)。特に高濃度の分散系では、界面活性剤や高分子分散剤の吸着層を粒子表面に形成して分散安定化を図ることが不可欠である23),24)。従って粘度特性を検討する際には、この吸着層の影響も考慮しなければならない。吸着層が粒子の分散状態を変化させれば、当然粘度は変化するであろう2),23)。しかしそれだけでなく、たとえ分散状態が同じであっても、吸着層によって粒子の実効体積が変われば、分散液の粘度特性が影響を受けることは充分予想できることである。吸着層が薄い場合は影響は小さいかもしれないが、立体反発力を生じるほどの高分子吸着層では吸着層膜厚が粒子の大きさに対して無視できなくなるはずで24)、その場合には粒子の体積だけでなく吸着層の厚さも考慮した流動特性の解析が必要になるであろう。ところが現実には吸着層膜厚の実測が困難なため、粒子の実効体積と粘度の関係を定量的に解析した例はほとんどなく、逆に粘度の測定値から吸着層膜厚を推定するにとどまっている21)。
前章で述べたように、本研究では粒子表面に形成した樹脂吸着層の厚さの実測に成功している。そこで、本章ではこれらの分散液を用いて磁性粒子分散系の粘度特性を解析し、その特徴を明かにすることを試みた。その際に、樹脂吸着層の体積も考慮に入れた固体成分の体積分率という考え方を導入し、また粘度を評価する方法として、分散系での相対粘度、換算粘度という値を定義する。これらの数値を用いることによって、樹脂や溶媒の種類が異なる分散液に対しても、統一的に流動特性が解釈できることを示す25)。
2. 実験方法
2.1 試 料
磁性粒子は針状γ-酸化鉄、およびバリウムフェライト、エポキシ樹脂は分子量2900のビスフェノール-A型のもので、第1章と同じである。溶媒としては、第1章で用いた2種に加えてブトキシエタノールも使用した。
2.2 分散液の調製
磁性粒子分散液は、第1章、第2章に示した方法で調製した。分散液に対してRehacekの手法26)を適用して求めた樹脂吸着層に関するデータを、Table1およびTable2に示す。Table1は針状γ-酸化鉄、Table2は板状バリウムフェライトについての測定結果である。
Table 1 Parameters of epoxy-resin adsorbed layer on acicular γ-Fe2O3.
| Parameter |
Resin Molecular
weight |
Resin amount
(mg/g) |
Solvent amount
(mg/g) |
Thickness
(nm) |
Solvent :
Cyclohexanone |
2900 |
111 |
372 |
22 |
| 2900 |
95 |
296 |
18 |
| 2900 |
51 |
232 |
13 |
| 2900 |
44 |
149 |
9 |
| 2900 |
42 |
180 |
10 |
| 2900 |
29 |
103 |
6 |
| 2900 |
25 |
55 |
4 |
| 3800 |
60 |
225 |
13 |
| 900 |
41 |
98 |
6 |
| 900 |
25 |
51 |
4 |
Solvent :
2-Ethoxyethyl acetate |
2900 |
110 |
239 |
16 |
| 2900 |
66 |
127 |
9 |
| 2900 |
54 |
127 |
8 |
Solvent :
Butoxyethanol |
2900 |
99 |
214 |
14 |
| 2900 |
35 |
89 |
6 |
Table 2 Parameters of epoxy-resin adsorbed layer on platelet Ba-ferrite.
| Parameter |
Resin Molecular
weight |
Resin amount
(mg/g) |
Solvent amount
(mg/g) |
Thickness
(nm) |
Solvent :
Cyclohexanone |
2900 |
135 |
410 |
18 |
| 2900 |
72 |
227 |
10 |
| 2900 |
67 |
134 |
7 |
| 2900 |
41 |
99 |
4 |
Solvent :
2-Ethoxyethyl acetate |
2900 |
143 |
227 |
12 |
| 2900 |
88 |
159 |
8 |
| 2900 |
74 |
193 |
9 |
試料の吸着樹脂量は25mg/gから100mg/g以上まで、膜厚にして4nmから22nmにわたっている。吸着層膜厚が4nm以下の試料も作成できるが、分散状態が極端に悪くなり、粘度特性検討用としては不適当である。
2.3 粘度特性の測定
粘度特性は、HAAKE社製、ロトビスコRV-12型回転粘度計を用いて測定した。ローターの外径は44.7mm、外筒との間のクリアランスは1mmで、回転数を0〜512min-1の範囲で連続的に変化させることができる。従って、剪断速度の可変範囲は、0〜1198s-1となる。粘度の測定では、試料を測定器に取り付けたときに試料内に残っているわずかな流れ等が測定に影響を与えることがある。そこで本研究では、試料をセットしてから6秒間静置した後、3分で所定の回転数まで上げ、6秒間保持、さらに同じ速度変化率で回転数を0まで落とすというサイクルを2回繰り返し、2回目のデータを流動曲線として採用することにした。また、曲線の解析は、剪断速度増加時の曲線に対して行なった。
3. 結果と考察
3.1 流動曲線の形状
磁性粒子分散液の典型的な流動曲線をFig.1に示す。曲線の形は、降伏値を持ち、やや上に凸の擬塑性流動の特徴を示している。また、剪断速度の増加時と減少時とで応力値が異なり、チキソトロピー性を持っていることがわかる。
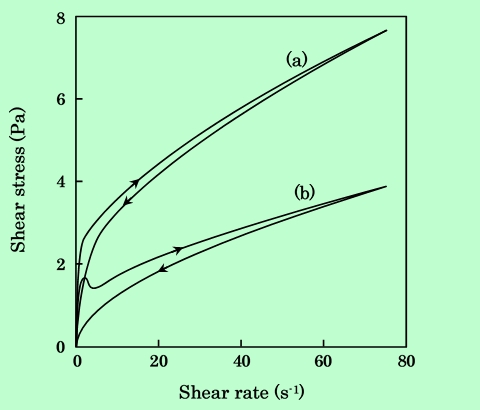
Fig.1 Typical shear rate - shear stress curves of magnetic particle dispersions
in cyclohexanone (a) and 2-ethoxyethyl acetate (b).
Epoxy-resin adsorbed amounts are 51 mg/g (a) and 54 mg/g (b).
吸着樹脂量がほとんど同じでも、溶媒によって応力の値や曲線の形状がかなり異なっており、シクロヘキサノンを溶媒として用いた方が、剪断応力値は大きく、またチキソトロピー性は小さくなっている。また、酢酸2-エトキシエチルを用いた場合には剪断応力の立ち上がりの部分に小さいピークが見られる。このピークの状態は、剪断速度の立ち上がりの速さによって変化する。その様子をFig.2に示す。立ち上がりが速すぎる場合は測定装置の応答が遅れて正しい情報が得られないが、その他の場合は剪断速度の立ち上がりが遅くなるほどピークは小さくなる傾向があり、粘弾性的な性質を持っていることがわかる。
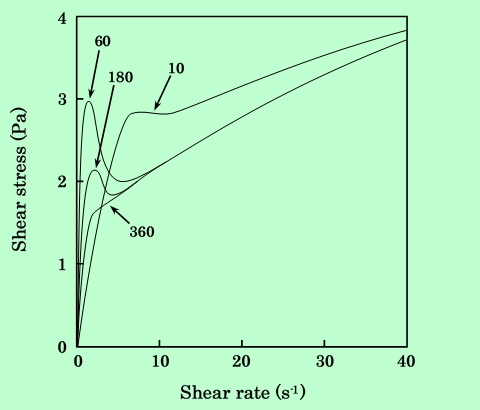
Fig.2 Dependence of curve shape on shear rate acceleration. Total seconds
required to obtain shear rate of 75 s-1 are shown in figure.
降伏値の存在や、その部分に見られる粘弾性的性質から、静置状態の分散液中には弱い弾性構造が形成されていることが推察される。この構造は、5s-1程度の剪断速度で簡単に破壊されるもので、シクロヘキサノン中よりも酢酸2-エトキシエチル中で顕著に現れると言える。また、これとは別のさらに強固な構造も形成されているようで、この構造がより速い剪断速度の領域で徐々に破壊されてチキソトロピー性を発現するものと思われる。
以上は流動曲線の定性的な解釈であるが、さらに定量的に扱うためには、特徴を記述する客観的な特性値を用いなければならない。Fig.1のような曲線を記述するための多数の式が提唱されているが7),9),10),15、本研究では最も一般的なものの一つであるCassonの式8)を適用することにする。ただし剪断速度の非常に小さい領域に関しては、挙動が複雑で測定条件の影響も受けやすいので27)、検討対象から除外した。従って、ここで扱う降伏値は真の降伏点ではなく、高剪断速度のデータを外挿して求められるみかけの値である。Cassonプロットの例をFig.3に示す。
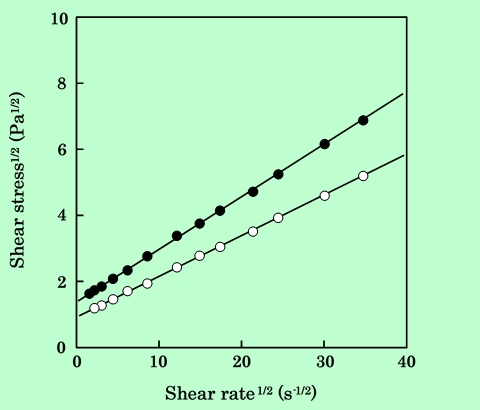
Fig.3 Examples of Casson plot. The samples are the same as in Fig.1. Solvents used
are cyclohexanone (black circles) and 2-ethoxyethyl acetate (white circles).
この図に示されているように、剪断速度が4s-1以下の低剪断領域を除けば、Cassonプロットは非常に直線性がよい。このグラフの縦軸切片の2乗が降伏値、傾きの2乗が、剪断速度無限大における粘度に相当する値、η∞である。(η∞のことを極限粘度、粘稠度、あるいは残留粘度などと呼ぶこともある。)このようにして得たη∞と降伏値を用いて、以下に分散液の粘度特性を解析して行く。
3.2 分散液粘度の検討
コロイド分散系の粘度は粒子濃度によって変化し、様々な分散系について粘度の粒子濃度(主として粒子体積分率)依存性が検討されている13)。本研究で扱っている系でも、粒子濃度は粘度特性を決定する重要な因子になるであろう。ただしここでは分散系内に樹脂が含まれており、しかもその一部は粒子表面に、残りは液中に存在しているため状況がかなり複雑で、粒子濃度や粘度の解釈には注意が必要である。
まず初めに、単純に磁性粒子(針状γ-酸化鉄)の体積分率とη∞との関係をプロットしてみた。Fig.4にその結果を示す。粒子の体積分率の増加によって粘度が増加する傾向が一応認められる。しかし、樹脂の分子量や溶媒の違いによって分散媒を形成する溶液の粘度が変化し、また樹脂の磁性粒子への吸着量も種々異なるなど、試料の条件が統一されていないので、ここからはあまりはっきりした結論を出すことはできない。
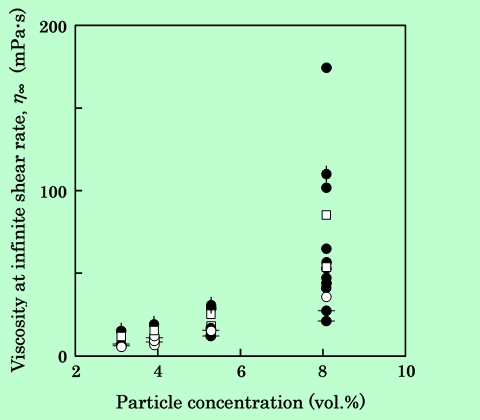
Fig.4 Viscosity at infinite shear rate,
η∞ of various dispersions.

: epoxy-resin molecular weight=900, Solvent=cyclohexanone

: epoxy-resin molecular weight=2900, Solvent=cyclohexanone

: epoxy-resin molecular weight=3800, Solvent cyclohexanone

: epoxy-resin molecular weight=2900, Solvent=2-ethoxyethyl acetate

: epoxy-resin molecular weight=2900, Solvent=butoxyethanol
磁性粒子表面に形成された樹脂吸着層は粒子と共に液中を移動するのであるから、流動性を解釈する際には固体分散質の一部と考えた方がよいであろう。この樹脂吸着層は厚いものでは20nm以上あり、粒子半径の80%に達するので、体積としてはかなりの大きさになる。そこで、粒子の体積と樹脂吸着層の体積を合わせて固体成分の体積分率を算出し、これをパラメーターにしてη∞を整理し直した。ここでの樹脂吸着層は、粒子と共に移動する部分であるから、吸着樹脂だけでなく吸着層中の溶媒も含めたものである。改めてプロットした結果がFig.5である。Fig.4と比較して、傾向が非常に明瞭になっており、固体成分体積分率という考え方が妥当であることを示している。溶液状の吸着層を剛体と見なすのはかなり大胆な仮定であるが、一次近似としては本質をよく表していると言えるであろう。
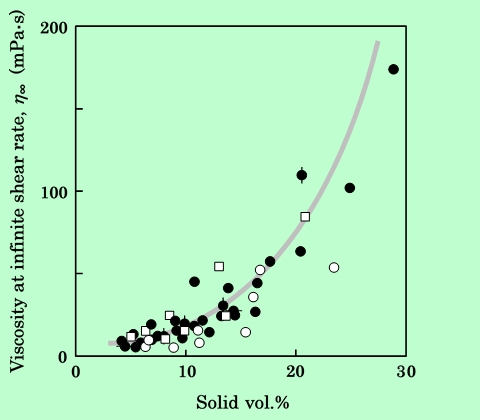
Fig.5 Dependence of η∞ on the volume fraction of solid component.
All symbols are the same as in Fig.4.
しかし縦軸の方にはまだ問題が残っている。固体成分の体積分率で粘度を評価するのであれば、液体成分の側の条件が影響しないように規格化しておかなければならない。一般に通常の高分子溶液の場合、溶液の粘度を溶媒の粘度で除した相対粘度を用いて流動特性を評価するが28)、この考え方を援用して、分散液の粘度を溶液バルクの粘度で除した値を、分散系の相対粘度、ηrelとして用いることにした29)。即ち、ηrel = η∞/ηliqである。ηliqは分散液から磁性粒子と吸着樹脂および吸着層中の溶媒を除いた残りの樹脂溶液の粘度であり、分散液を遠心分離した上澄み液の粘度を測定すれば得られる。このようにして得た相対粘度と、前に述べた固体成分体積分率との関係をFig.6に示す。ηrelを用いればFig.5よりもさらに相関がよくなり、溶媒や樹脂分子量に関係なく同じ基準で粘度を評価できることがわかる。
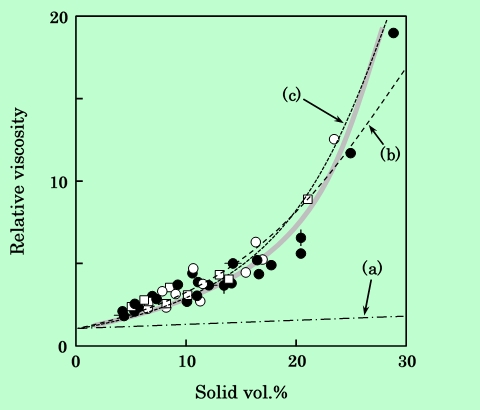
Fig.6 Dependence of relative viscosity on the volume fraction of solid component.
All symbols are the same as in Fig.4.
Curve (a), (b) and (c) correspond to equations
(a) : η = 1 + 2.5φ
(b) : η = 1 + 3.2φ + 166φ2
(c) : log η = 4.6φ
相対粘度 ηrelと固体成分体積分率 φ との間には、およそ図中に網かけの太線で示したような関係があるが、これがどのような関係式、いわゆる粘度式に当てはまるかを検討してみる。相互作用のない剛体球に関しては、次のEinstein式がよく知られている11)。
ηrel = 1 + 2.5φ (3.1)
これをプロットすると、図中の(a)のようになる。この式は粒子間相互作用の無視できる希薄分散液に対してしか適用できないので、当然今回の系からは大きくはずれる。粒子間相互作用も考慮に入れると、φ についての高次の項が必要になるが、2次の項までを取り入れた次の式が一般に用いられている30)。
ηrel = 1 + αφ + βφ2 (3.2)
ここでαは粒子の対称性によって決まる定数で、球形粒子の場合は2.5、非対称粒子では2.5<である。またβは粒子間相互作用を表す定数で、分散系の種類によって様々な理論値、実験値が求められており、例えばGuthらは14.1という値を得ている31)。式(3.2)を適用するために、Fig.6の実験値に対して縦軸切片が1という条件で2次回帰を行なうと図中の曲線(b)のようになり、得られた値はα=3.2、β=166であった。αの値は粒子の対称性から考えるとむしろ小さめであるが、βの値はGuthの値と比べても極端に大きい。この結果は、磁性粒子分散液中の粒子間相互作用が非常に大きいことを示している。φ >20%の領域ではηrelは曲線(b)よりもさらに急激に立ち上がっている。実験データに適合させるためには、式(3.2)にさらに高次の項を付加するか、または図中の曲線(c)のように指数関数を用いることが必要である。3次以上の高次項、あるいは指数関数の適用が必要ということは、粒子間相互作用が単に大きいだけでなく、φ の増加に伴って相互作用の形態が変化することを表している28)。おそらく φ の増加によって、液中に磁性粒子のネットワーク構造が形成されるのであろう18)。
粒子間相互作用をより明確にするために、高分子溶液では次のような換算粘度、ηredもよく用いられる28)。
ηred = {ηrel - 1}/φ (3.3)
粒子間相互作用がなければ、ηrelが φ について1次になるから、ηred は定数になる。一定の形式の相互作用のみであれば式(3.2)が当てはまるはずであるから、ηredは直線になるであろう。この考え方を本研究の系にも適用して、実際に ηred をプロットしたのがFig.7である。相対粘度、ηrel の傾向からも予測できるように、換算粘度、ηred は φ >20%で急激に増加する。この結果からも、磁性粒子分散液中に構造が形成されていることが推察される。
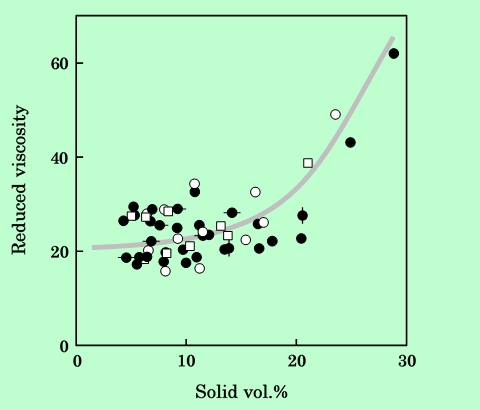
Fig.7 Dependence of reduced viscosity on the volume fraction of solid component.
All symbols are the same as in Fig.4.
磁性粒子の場合、磁気的な引力が粒子間相互作用の主要因の一つになっていることが考えられる。そこで粒子濃度によって2粒子間の磁気的引力がどのように変化するかを簡単なモデルで計算してみた。磁性粒子の磁化をその中心にある1個の磁気モーメントで近似し、2個の磁気モーメントが逆平行の形で接近するとして引力エネルギーを計算した結果をFig.8に示す。
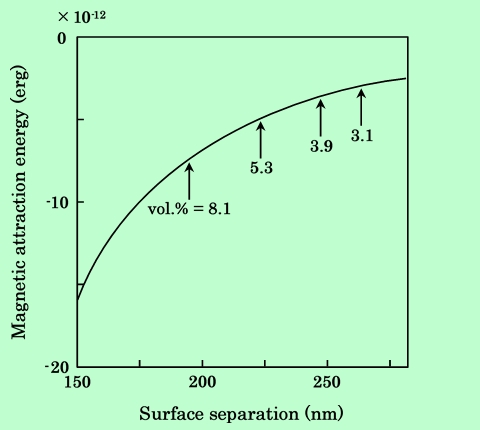
Fig.8 Magnetic attraction energy calculated with a simple dipole approximation.
Average surface separations between two magnetic particles in the dispersions
are shown in the figure.
実際に用いた分散液の粒子濃度における、2粒子間の平均距離も図中に示している。粒子濃度8.1vol.%と3.1vol.%では、約2倍のエネルギー差があり、濃度が増加するにつれて引力が急激に強くなることがわかる。従って、高濃度になるほど磁性の影響が強く現れることが予測される。
固体成分体積分率には、磁性粒子濃度、即ち粒子の数と、樹脂吸着層膜厚、即ち粒子一個一個の大きさの両方が寄与する。このうち樹脂吸着層膜厚の方は、磁気的相互作用には影響しない。一方、磁性粒子の濃度が変わると、粒子間の平均距離が変化するので、磁気的相互作用も変化し、粘度に何等かの影響を与えるはずである。そこで粒子濃度ごとに記号を変えてFig.6のデータを再プロットしてみた。その結果がFig.9である。
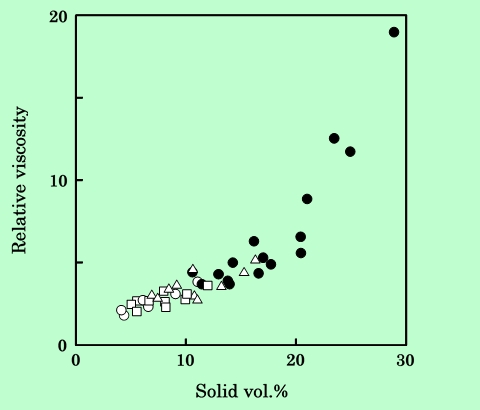
Fig.9 Relative viscosity of dispersions which particle concentrations are
3.1 vol.% (

), 3.9 vol.% (

), 5.3 vol.% (

) and 8.1 vol.% (

).
当然の結果として高濃度の試料が右寄りにプロットされることになるが、各濃度の試料がプロットされている領域は互いにかなり重なっており、全体として一つの曲線で表しても問題ないと言えるであろう。即ち、粒子濃度の変化と、吸着層膜厚の変化とは、粘度に対してほとんど同じように寄与するということである。この結果は、粘度を支配する主要因は固体成分体積分率であり、磁性の効果は小さい、ということを示している。本研究では、樹脂吸着層によって単分散に近い状態まで分散安定化した試料を用いているので、このような結果になったのであろう。分散性の悪い試料、あるいはさらに高濃度の試料を用いると、粒子の凝集などの問題も生じて、磁性の影響はより顕著になる可能性がある。実際にFig.9の高濃度領域では、構造形成に起因すると思われる急激な粘度の立ち上がりが見られるが、このあたりには磁気的相互作用の影響が現れ始めているのかもしれない。
3.3 降伏値の検討
Cassonプロットから得られる降伏値についても、相対粘度、換算粘度と同様に、固体成分の体積分率という観点で整理してみた。Fig.10にその結果を示す。
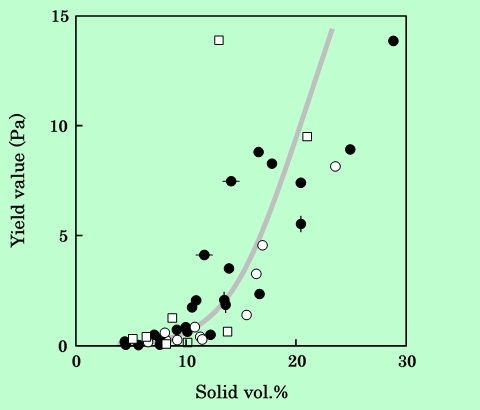
Fig.10 Dependence of yield value on the volume fraction of solid component.
All symbols are the same as in Fig.4.
降伏値に関してもよい相関があり、溶媒の種類や樹脂の分子量によらず、降伏値も一次近似的には固体成分体積分率によって決まることがわかる。粘度の場合は体積分率が20%を越えると急激に立ち上がる傾向が見られたが、降伏値の場合は約10%から立ち上がっている。降伏値は分散液が静止した状態で形成される弱い弾性構造を反映していると考えられるので、体積分率10%程度からこの構造形成が顕著になることが推察される。
Fig.10を粒子濃度ごとにプロットしたのがFig.11である。
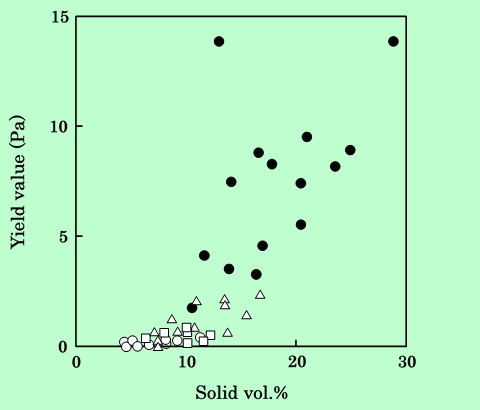
Fig.11 Yield value of dispersions which particle concentrations are
3.1 vol.% (○), 3.9 vol.% (□), 5.3 vol.% (△) and 8.1 vol.% (●).
各濃度ごとに曲線を引くと、粘度の場合と異なり、高濃度の試料に対する曲線がやや上にくる傾向があるように見える。従って、降伏値に関しては、吸着層膜厚よりも粒子濃度の方が影響が大きいということになる。このことは磁気的相互作用の関与を示唆しているのかもしれない。即ち、静止状態では磁気的相互作用が弾性構造の形成に寄与している可能性があるということである。
3.4 板状粒子の粘度特性
以上の針状γ-酸化鉄粒子に対して行なった解析手法を用いて、板状のバリウムフェライト粒子の粘度特性32),33)についても検討した。前節で定義した分散液の相対粘度と固体成分体積分率の関係をFig.12に示す。図中の記号はFig.4と同じである。溶媒による差がわずかに出ているように見えるが概ね相関はよく、板状粒子の場合も、樹脂吸着層を含めた固体成分体積分率が粘度を支配する主要な因子であることがわかる。
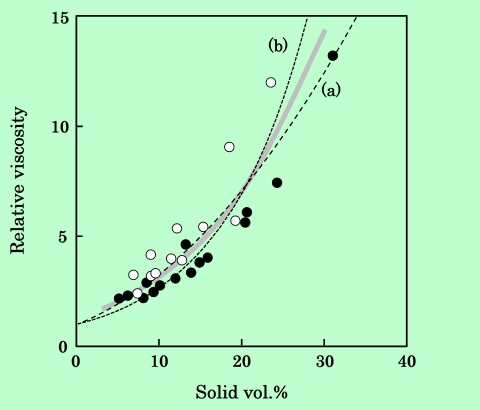
Fig.12 Dependence of relative viscosity of platelet particle dispersion on the
volume fraction of solid component. Epoxy-resin molecular weight is 2900.
Solvents are cyclohexanone (black circles) and 2-ethoxyethyl acetate
(white circles).
Curve (a) and (b) correspond to equations (a) : η = 1 + 14φ + 80φ2
and (b) : log η = 4.2φ
針状粒子の場合と同様に、このデータに対して、φ に対する2次関数、指数関数を当てはめた結果も図の中に示している。どちらの曲線でもほぼ同じような適合性を示しているが、高濃度領域での立上りは2次関数の方が実測値に近い。また2次関数の場合は、針状粒子と比べて1次の係数が大きく、2次の係数は小さくなっている。これらの結果から判断すると、粘度に対して、板状粒子では粒子一個一個の形状による寄与が大きく、粒子間相互作用の寄与は小さいことになる。このことは換算粘度にも現れており、Fig.13に示すように、濃度の増加に対して換算粘度が急激に上昇する様子は観測されていない。即ち、針状粒子に見られたような、或る濃度領域から構造形成によって急激に粒子間相互作用が大きくなる、という現象は起こっていない。しかしながら直ちに、これが板状粒子の流動の特徴である、とは言いきれない。第1章でも述べたように、板状粒子は針状粒子に比べて凝集しやすいため、常にいくらかの凝集塊が存在すると考えた方がよく、ここで現れている流動の特徴も、ある程度の凝集状態における結果と考えるべきであろう。
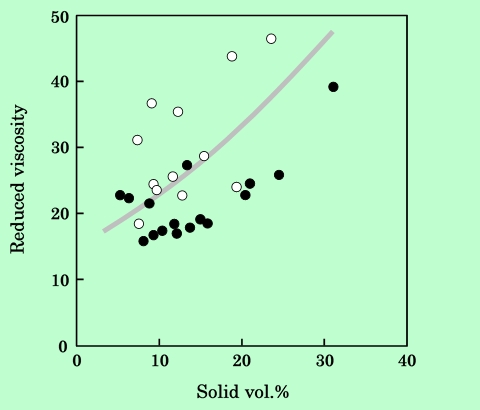
Fig.13 Dependence of reduced viscosity of platelet particle dispersions on the
volume fraction of solid component. Conditions are the same as in Fig.12.
Cassonの降伏値についても同様に固体成分体積分率に関して整理した。結果をFig.14に示す。
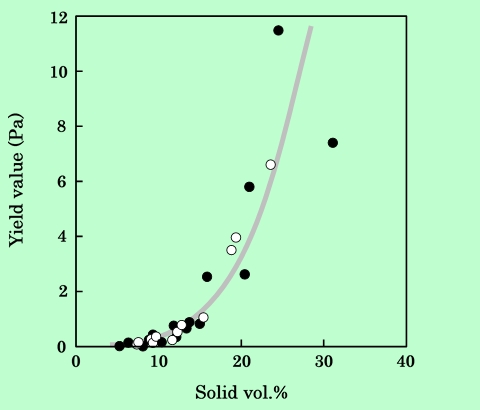
Fig.14 Dependence of yield value of platelet particle dispersions on the volume
fraction of solid component. Conditions are the same as in Fig.12.
ここでも非常によい相関が得られており、溶媒によらず全体が一つの曲線上に乗っている。ただし降伏値の場合は、粘度の場合と違って針状粒子と傾向がよく似ており、固体成分体積分率10%付近から急激に立ち上がる様子が見られる。分散液中で、磁気的相互作用も関与した構造形成が起こっているのではないかと思われる。
4. 結 言
針状γ-酸化鉄粒子および板状バリウムフェライト粒子を用いて、粒子濃度、有機溶媒の種類、分散剤樹脂の分子量、粒子表面の樹脂吸着層といった条件の異なる種々の分散液を調製し、その粘度特性を検討した。分散液の流動曲線は擬塑性流動の形を示し、Cassonの式によく当てはまるので、Cassonプロットの傾きとして得られる粘度と、切片として得られる降伏値によって評価した。
分散液の中で、溶媒も含めた樹脂吸着層と磁性粒子とを合わせて固体分散質と考え、残りの樹脂溶液を分散媒とすると、高分子溶液における相対粘度、換算粘度の考え方を分散系にも援用できることがわかった。即ち、相対粘度、換算粘度、および降伏値を固体成分体積分率に対して整理すると、溶媒の種類や樹脂の分子量によらず、全ての分散液に関する測定値を一つの曲線上にプロットすることができる。これらの曲線を解析した結果、磁性粒子の分散液中では粒子間相互作用はかなり大きく、濃度の増加と共に液中に構造が形成されてさらに相互作用が急増すること、相互作用の急増点は針状粒子では体積分率約20%のところであるが、板状粒子では明瞭に現れないこと、降伏値は針状粒子、板状粒子共に体積分率約10%のところから急増すること、さらに磁気的引力の影響は分散性の良好な液では顕著に現れないことが明らかになった。
文 献
1)S.Dasgupta, IEEE Trans. Magn., MAG-20, 7 (1984)
2)J.W.Gooch, Coating Tech., 60, 37 (1988)
3)松本孝芳, 表面, 25, 590 (1987)
4)乙竹 直 "サスペンションを中心とした分散技術と工業的応用の実際 総合資料集", p184, 分散技術研究会 編, 経営開発センター出版部 (1978)
5)K.Hattori and K.Izumi, J. Dispersion Sci. Tech., 11, 307 (1990)
6)淵上修三, "分散系レオロジーと分散化技術", p257, 梶内俊夫, 薄井洋基 編, 信山社出版 (1991)
7)E.C.Bingham, "Fluidity and Plasticity", McGraw-Hill, New York (1922)
8)N.Casson, "Rheology of Dispersion Systems", p84, C.C.Mill, Pergamon Press, London (1959)
9)M.M.Cross, J. Colloid Interface Sci., 33, 30 (1970)
10)T.Matsumoto, A.Takashima, T.Masuda and S.Onogy, Trans. Soc. Rheol., 14, 616 (1970)
11)A.Einstein, Ann. In. Phys., 19, 289 (1906)
12)S.Yao and T.Matsumoto, J. Non-Newtonian Fluid Mechanics, 25, 197 (1987)
13)Ir.R.Rutgers, Rheol. Acta., 2, 305 (1962)
14)A.Voet and R.Suriani, J. Colloid Sci., 6, 155 (1951)
15)M.Mooney, J. Colloid Sci., 1, 195 (1946)
16)T.L.Smith and C.A.Brouce, J. Colloid Interface Sci., 72, 13 (1979)
17)W.Nagashiro and T.Tsunoda, J. Appl. Polymer Sci., 25, 2961 (1980)
18)P.N.Kuin, IEEE Trans. Magn., MAG-23, 97 (1987)
19)S.Watanabe, Ferrites:Proceedings of International Conference, July 1970, Japan, 473 (1970)
20)尾崎正孝, 高松宏一, 日本化学会誌, 1960 (1988)
21)韓 基洙, 増子 徹, 第34回レオロジー討論会 講演予稿集, 201 (1986)
22)中前勝彦, 表面, 25, 401 (1987)
23)H.Inoue, H.Fukke, M.Akagi and M.Katsumoto, J. Magn. Magn. Mater., 118, 263 (1993)
24)H.Inoue, H.Fukke, M.Katsumoto and K.Konno, J. Colloid Interface Sci., 138, 92 (1990)
25)H.Inoue and M.Katsumoto, J. Magn. Magn. Mater., 125, 377 (1993)
26)K.Rehacek, Farbe Lack, 76, 656 (1970)
27)長瀬洋一, 粉体工学会誌, 23, 46 (1986)
28)灰佐雅夫, "高分子", p32, 東京化学同人 (1967)
29)野呂俊一, "サスペンションを中心とした分散技術と工業的応用の実際 総合資料集", p209, 分散技術研究会 編, 経営開発センター出版部 (1978)
30)H.L.Frisch and R.Simha, "Rheology, Theory and Application", Vol.1, Chap.14, F.R.Eirich, Academic Press, New York (1956)
31)E.Guth and R.Simha, Kolloid-z., 86, 105 (1939)
32)T.M.Kwon, M.S.Jhon and T.E.Karis, J. Mag. Soc. Jpn., 15, 663 (1991)
33)T.E.Karis and M.S.Jhon, Colloid and Surfaces, 53, 393 (1991)
目 次
雑科学ホーム
hr-inoueホーム














