
目 次
雑科学ホーム
hr-inoueホーム

Back
4. 計算結果と考察
4.1 各要素エネルギーの比較
Parallel配置の針状粒子、Series配置の板状粒子について、前節で述べた改良された計算方法によって求めた磁気的引力エネルギー、立体反発エネルギー、van der Waalsエネルギーの値をFig.18に示す。引力エネルギーは通常は負の値で表すが、ここでは比較のためにすべて正の値で示している。計算に用いるパラメーターは Table1のとおりである。
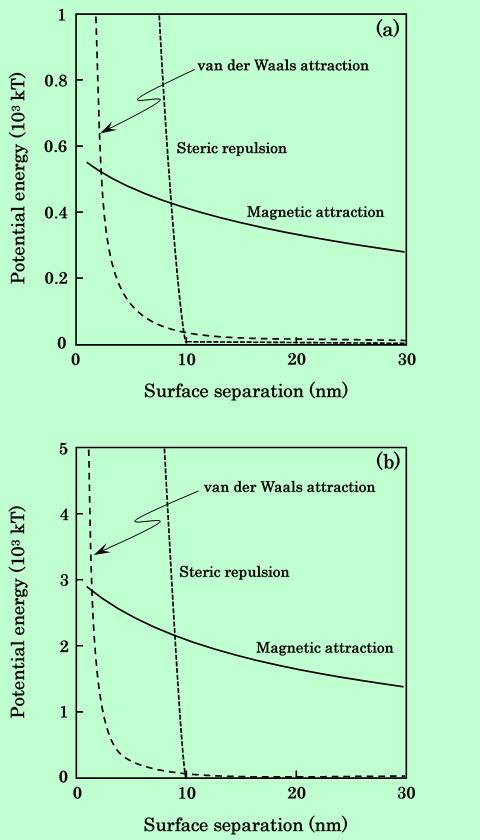
Fig.18 Three elements of potential energy between
(a) parallel aligned acicular particles and (b) series aligned platelet particles.
立体反発エネルギーは樹脂吸着層が重なり始めると同時に急激に立ち上がり、磁気的引力エネルギーを上回るようになる。van der Waalsエネルギーも5nm付近から立ち上がるが、2nmまで粒子が接近しても立体反発エネルギーを越えるには至っていない。また吸着層が重ならない領域では、磁気的引力だけが粒子間に働いていると言ってよいであろう。従って、距離が遠いときは磁気的引力エネルギー、吸着層が重なり始めると立体反発エネルギーが相互作用を支配し、van der Waalsエネルギーが問題になるのは非常に近距離の場合のみ、と言うことができる。
4.2 粒子形状の影響
これまで粒子形状に関しては、形状比6の針状粒子と形状比0.2の板状粒子についてのみ検討してきた。ここでは形状比を種々変化させて、磁気的エネルギーの違いを調べてみる。Fig.19はParallel配置、Fig.20はSeries配置の場合の計算結果である。またFig.21〜23は形状比をパラメーターとした時のエネルギーの変化を、3種類の粒子表面間距離についてプロットしたものである。Parallel配置では形状比が1の時が最も磁気的引力が強くなるが、Series配置ではそれよりも偏平な、形状比0.3〜0.4付近に極大(エネルギーでは極小)があることがわかる。また、ここで扱った形状比、粒子間距離の範囲では、Series配置の方が引力が強いことも示されている。
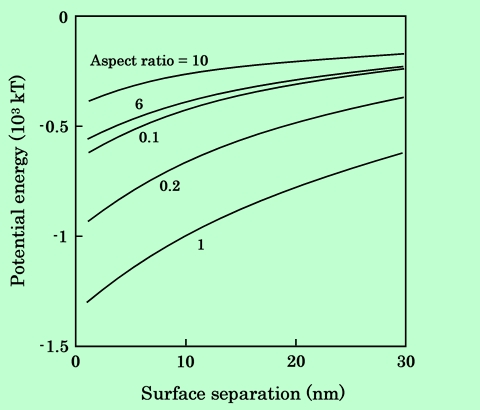
Fig.19 Effect of aspect ratio on magnetic attraction energy.
Magnetic particles are aligned in parallel.
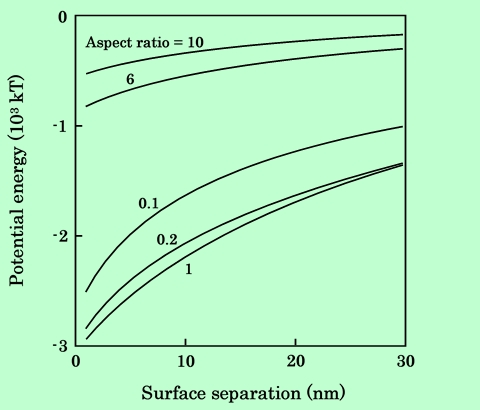
Fig.20 Effect of aspect ratio on magnetic attraction energy.
Magnetic particles are aligned in series.
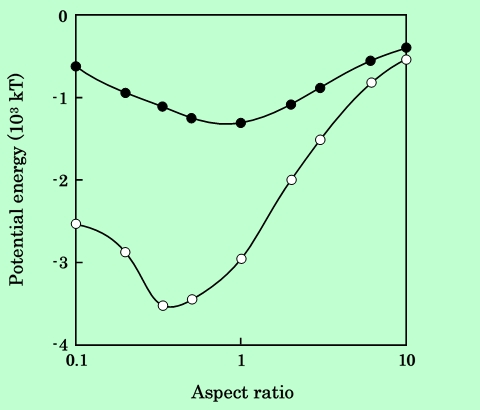
Fig.21 Aspect ratio dependence of magnetic attraction energy at surface
separation of 1 nm. Black circles are for parallel aligned particles
and white circles are for series aligned ones.
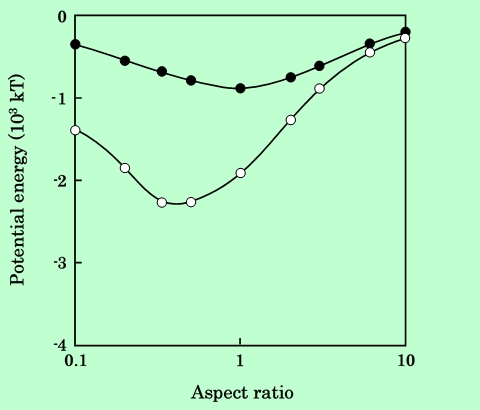
Fig.22 Aspect ratio dependence of magnetic attraction energy at surface
separation of 15 nm. Black circles are for parallel aligned particles
and white circles are for series aligned ones.
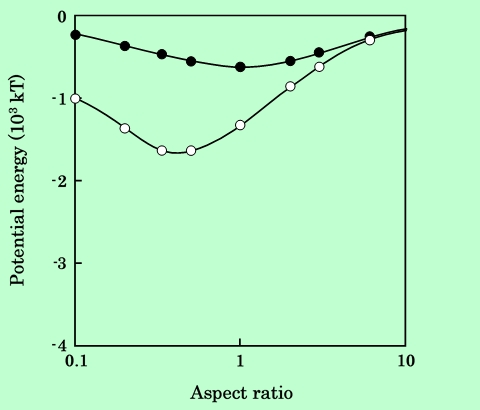
Fig.23 Aspect ratio dependence of magnetic attraction energy at surface
separation of 30 nm. Black circles are for parallel aligned particles
and white circles are for series aligned ones.
この結果だけから判断すると、双極子モデルによる計算結果とは異なり、針状粒子も板状粒子もSeries型に、即ち磁気モーメントを同じ方向に向けて一列に凝集する形をとり易いことになる。しかしながら形状比が大きいところでは2種類の配置のエネルギー差はかなり小さい。しかも針状粒子が縦に連なった形の凝集は、撹拌などの機械的な力によって破壊される可能性が高い。従って、撹拌によって分散状態が保たれているような針状粒子の分散系では、むしろParallel配置の方が主要な凝集形態なのではないかと考えられる。実際に、第1章、第2章のTEM写真が示すように、形状比6の針状粒子を分散させた系では粒子は主としてParallel配置で凝集しており、その一次凝集体がSeries配置の凝集で連結されるような形をとることが多い。
これに対して形状比が1以下の板状粒子では、磁気的エネルギーの計算結果から見ても、また機械的な凝集破壊の困難さから見ても、Series配置が圧倒的に有利であることは容易に理解できる。このことを示す実例の一つとして、第1章で述べた方法で調製した板状粒子分散液のTEM写真をFig.24に示す。

Fig.24 TEM images of platelet particle dispersions.
(a) before dilution, (b) after dilution.
多数の粒子がSeries配置で長く連なった、いわゆるスタッキングと呼ばれる凝集体を形成しているのがわかる。また、中にはこのスタッキングが長く延びて、磁気的に非常に安定であると思われる閉じたループを作っている部分も見られ、磁気的引力の影響が顕著に現れていると言える。このように種々の形状をした粒子の実際の凝集形態を、磁気的エネルギーの計算を基にして、ある程度解釈することが可能である。
4.3 粒子サイズの影響
粒子サイズの影響に関しては双極子モデルでも検討したが、ここでは精密化した計算方法に基づいて再検討する。Fig.25は形状比6の針状粒子についての結果である。曲線の形は双極子モデルの場合(Fig.5)とほとんど同じであるが、エネルギーの絶対値はかなり違っている。双極子モデルでは2次極小の絶対値は数千kTにもなるが、セル分割モデルでは一桁小さい。これは、双極子モデルによる計算が磁気的引力を過大に見積もっているためである。逆に極大値は、磁気的引力が小さくなった分だけセル分割モデルの方が大きいが、van der Waals引力も計算の精度を上げることで大きくなっているので比較的遠距離から1次極小に向かって落ち込むようになる。
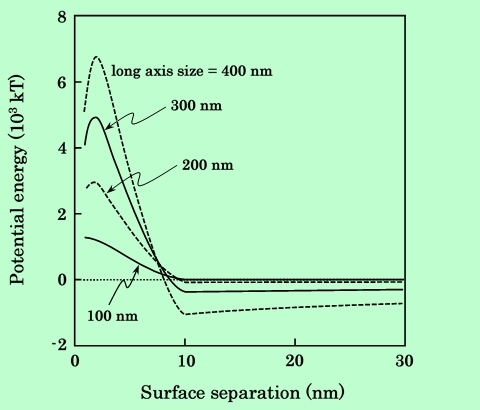
Fig.25 Effect of particle size on potential energy between two acicular particles.
Fig.25から、粒子サイズが大きくなると立体反発力は大きくなるが、2次極小もより深くなる、ということがわかる。この傾向は双極子モデルの場合と同じであるが、今回は計算の精度が上がっているので、傾向だけでなく絶対値も考慮して、磁性粒子の分散性を検討してみる。反発エネルギーの極大値は、長軸長が100nmの粒子でも1000kT以上あり、この障壁を越えて粒子が接近することは考えられない。従って、凝集に直接かかわるのは2次極小である。粒子の長軸長が400nmの場合、2次極小は-1000kTもあり、この位置で凝集した粒子を再分散させることはほとんど不可能である。長軸長が300nmおよび200nmになると、2次極小はそれぞれ-430kT、-120kT程度まで下がるが、やはり再分散は難しい。しかし長軸長が100nmまで小さくなると2次極小は-13kTとなり、熱運動エネルギーに近いオーダーとなるので、撹拌などの操作によって再分散も可能であろう。
実際に微細粒子を第1章と同じ方法で分散させた例を、Fig.26に示す。ここで用いている粒子は長軸長100〜200nm、比表面積が50m2/gの針状γ-酸化鉄で、吸着樹脂量は80mg/g、吸着層膜厚は8nmである(算出法は第2章参照)。第1章のFig.11に示した長軸長300nmの粒子(吸着層膜厚は最も薄いものでも12nmある)と比較して、吸着層が薄いにもかかわらず、微細粒子の方が分散性が良好であることがわかる。

Fig.26 TEM images of fine particle dispersions.
(a) before dilution, (b) after dilution.
板状粒子について、同様に粒子サイズの影響を検討したのがFig.27である。形状比は0.2で、Fig.25の針状粒子と同じ体積になるように粒子の大きさを設定している。針状粒子の場合と傾向は同じであるが、極大も2次極小も約5倍大きくなっていることがわかる。2次極小の値は、粒子サイズの大きい方から順に、-5300kT、-2100kT、-560kT、-50kTで、最も小さい粒子でも再分散はかなり難しいと言える。
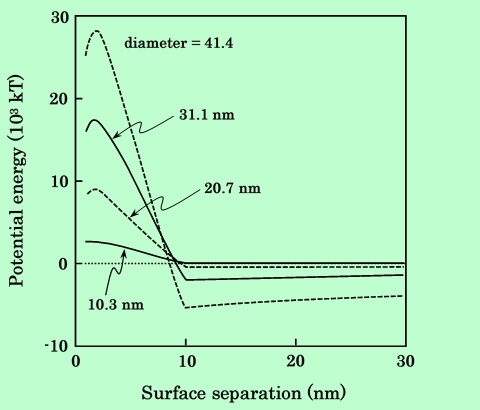
Fig.27 Effect of particle size on potential energy between two platelet particles.
4.4 樹脂吸着層膜厚の影響
樹脂吸着層の厚さが粒子の分散性に大きな影響を与えることは、前章までに述べてきたように実験的にも確認されている。ここでは粒子間ポテンシャルの面から、吸着層膜厚がどのように影響するかを調べてみる。Parallel配置の針状粒子についての結果をFig.28に示す。
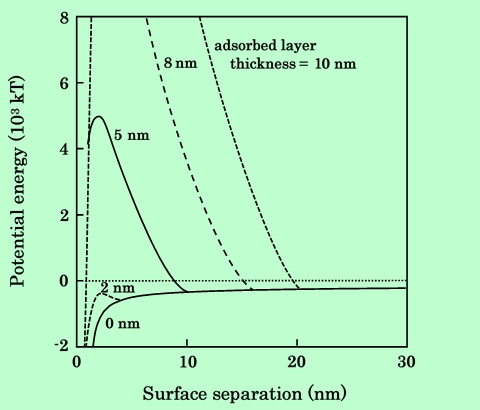
Fig.28 Effect of adsorbed layer thickness on potential energy between
two acicular particles.
注目されるのは、樹脂吸着層の膜厚が2nm以下では粒子間ポテンシャルが反発の領域に入らない、ということである。この状態では、2次極小の位置で凝集した粒子は、無限遠に離れて行くのとほぼ同じ確率で1次極小側に落ち込むことになるので、再分散の可能性はほとんどなくなるであろう。吸着層が厚くなってくると反発のエネルギー障壁は高くなり、1次極小に落ち込む可能性は少なくなる。ただし膜厚が5nmもあれば、既に容易には越えられない高さの障壁ができており、これ以上に障壁を高くしても1次極小への落ち込み防止効果はさほど変わらないと思われる。しかし2次極小に注目すると、吸着層を厚くすることで極小を浅く、また遠い位置へ持って行くことができるので、この点では分散安定化の効果、凝集を遅らせる効果が期待できるであろう。また、仮に2次極小の位置で凝集したとしても、粒子間には吸着層膜厚の2倍に相当する距離が保たれるので、分散液の磁気的な特質を損なうような強固な凝集体の形成は避けられる可能性が大きい。
板状粒子の場合も傾向はほとんど同じであるが(Fig.29)、エネルギーの絶対値は針状粒子の場合よりも大きい。極大値について見てみると、吸着層膜厚2nmでも既に反発領域にはいっているので、吸着層が薄い時に1次極小に落ち込む確率は針状粒子よりも低いと言えるであろう。しかし、凝集を考える上で最も重要と思われる2次極小については、同じ吸着層膜厚で比較すると針状粒子よりも約5倍深くなっており、より凝集傾向が強いことが予想される。

Fig.29 Effect of adsorbed layer thickness on potential energy between
two platelet particles.
4.5 磁化量の影響
これまでの計算では磁性粒子の磁化量(磁気モーメントの大きさ)はすべて75emu/gとしている。この値は、ほぼγ-酸化鉄の磁化に相当するが、その他の磁性粒子では当然磁化量も異なってくる。例えば、マグネタイトでは92emu/g、バリウムフェライトでは50〜65emu/g、二酸化クロムでは123emu/g、純鉄では220emu/gなどである。磁気的相互作用は磁化の2乗に比例するので、粒子間ポテンシャルは磁化量に大きく影響されることが予想され、球形の鉄粒子の磁気的引力エネルギーがγ-酸化鉄粒子の17倍になるという計算結果も報告されている32)。そこで種々の磁化量の針状粒子について粒子間ポテンシャルを計算し、その分散性を検討した。磁化量は0(非磁性粒子)から、実用的な鉄粒子に相当する125emu/g(表面酸化膜のために純鉄の値よりも小さい。後述)まで変化させている。計算結果をFig.30に示す。非磁性粒子では2次極小値は-28kTしかなく、撹拌等の操作による再分散も不可能ではない値であるのに対し、磁化量50emu/gの粒子では-210kT、磁化量125emu/gの粒子では-1150kTにも達する。非磁性粒子と比較して、磁性粒子の分散がいかに困難であるかがわかる。
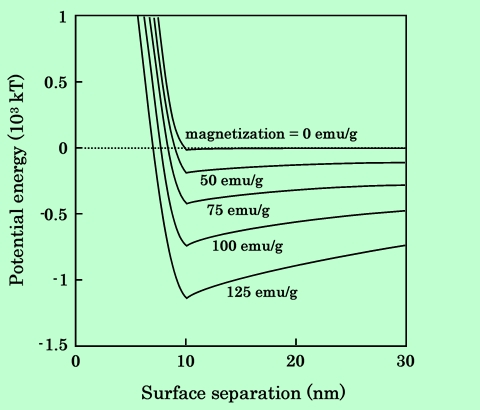
Fig.30 Effect of magnetization on potential energy between two acicular particles.
Fig.30に示した計算では、鉄粒子に相当する値として125emu/gを用いた。純鉄の磁化量は220emu/gであるが、実際の鉄粒子では酸化を抑制するために粒子表面に非磁性の酸化層が形成されており33),34)、これによって磁化量が大幅に低下しているからである。従って、厳密には鉄粒子は均一組成ではなく、中心に純鉄の核、周囲に非磁性酸化鉄の殻を持った構造をしていることになる。そこで、非磁性酸化鉄層の厚さを種々変化させて、現実の鉄粒子に即したモデルで粒子間ポテンシャルを計算し直してみた。酸化膜の厚さは均一で、粒子の短軸半径に対して0%、10%、25%、40%、50%に設定した。中心の鉄の密度を7.9g/cm3、酸化膜の密度を5.2g/cm3として粒子の平均磁化量を計算すると、それぞれ220emu/g、191emu/g、146emu/g、101emu/g、74emu/gとなる。ポテンシャルエネルギーの計算結果をFig.31に示す。
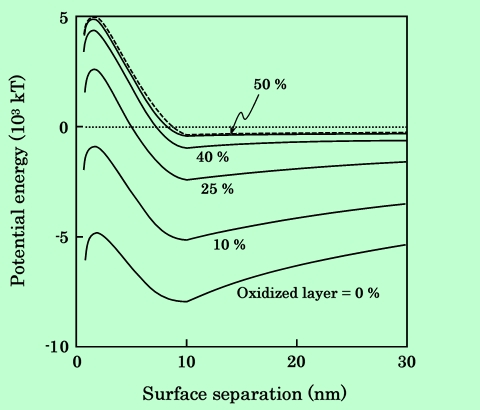
Fig.31 Effect of oxidized layer thickness on potential energy between two acicular
Fe particles. Broken line shows the potential curve of γ-Fe2O3 (75 emu/g).
酸化膜のない純鉄の場合には2次極小値は-8060kTで、γ-酸化鉄(-430kT)の約19倍になっている。酸化膜が厚くなるにしたがって引力エネルギーは急激に低下し、酸化膜厚が粒子半径の50%になるとγ-酸化鉄とほぼ同等になることがわかる。しかしこの時点では既に平均磁化量もγ-酸化鉄と同じところまで下がっており、鉄粒子の利点は無くなっている。またこの結果から、鉄粒子の粒子間ポテンシャルを計算する場合に、中心の鉄と周囲の酸化膜とに分けて考えなくても、平均の磁化量でほぼ正確な値が得られることが確認できた。
4.6 樹脂分子量の影響
第2章で、吸着層を形成する樹脂の分子量が磁性粒子の分散性に与える影響について実験的に検討したが、ここでは実験で得た樹脂吸着層に関するデータを基にして粒子間ポテンシャルを計算し、分散性に対する樹脂分子量の影響を調べてみた。同じ条件で磁性粒子分散液を調製した場合、樹脂の分子量が大きいほど吸着重量は増加し、吸着層中の樹脂濃度は小さくなり、吸着層膜厚は増加する(第2章参照)。Table2にこれらのパラメーターを改めてまとめておく。
Table 2 Parameters of resin adsorbed layer
| Molecular weight |
500 |
900 |
1400 |
2900 |
3800 |
| Resin amount (mg/g) |
27.5 |
29.2 |
30.5 |
38.3 |
50.0 |
| Resin wt.% |
41 |
32 |
26 |
22 |
21 |
| Thickness (nm) |
3.0 |
4.2 |
5.3 |
8.1 |
10.8 |
これらのデータを用いて粒子間ポテンシャルを計算した結果をFig.32に示す。
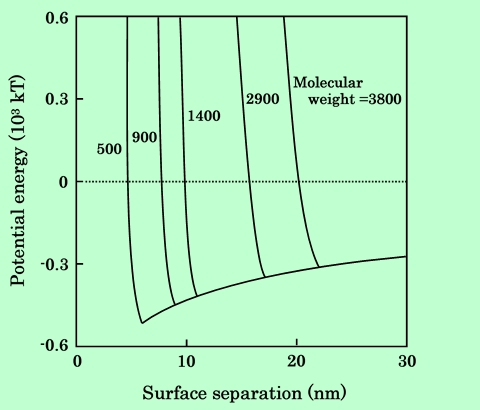
Fig.32 Effect of resin molecular weight on potential energy between parallel
aligned acicular particles.
樹脂分子量が小さい方が吸着層中の樹脂濃度が大きいので、吸着層の重なりによる反発エネルギーは大きくなる。しかし図からわかるように反発領域へ向かっての立ち上がりは非常に急激で、簡単に1000kT以上の充分な反発エネルギーが得られるので、極大値の大小関係が問題になることはないであろう。一方、立ち上がりの位置は吸着層が重なり始める位置、即ち吸着層膜厚によって決まるため、吸着層の厚い高分子量樹脂の方が遠くに来る。それだけ粒子は大きく隔てられるわけで、例えば分子量3800の樹脂を用いた場合には、2個の磁性粒子は22nm以下には接近できないことになり、分散性の向上に有利に働くことが期待される。実際に高分子量の樹脂を用いた方が分散性がよくなることは、第2章で述べたとおりである。
4.7 溶媒の影響
溶媒の種類によって磁性粒子への樹脂の吸着状態が変わり、分散性も変化することは、第1章、第2章でも述べた。そこで、シクロヘキサノンと酢酸2-エトキシエチルという2種類の溶媒について、粒子間ポテンシャルの面から検討してみた。その際に、溶媒が異なる分散液をどのような条件で比較するか、ということが問題である。同じ条件で分散液を調製すると、酢酸2-エトキシエチルを用いた方が吸着樹脂量が多くなることが実験的に確かめられている(第1章参照)。このことから考えると、試料作製条件を同じにして、それぞれの溶媒における吸着樹脂量の実験値を用いて計算するのが妥当なように思われる。しかし、溶媒によって吸着樹脂量が異なるのは物理吸着量が異なるからである。物理吸着樹脂は希釈などの操作によって簡単に脱離することから、吸着層が重なったときにも脱離を起こしてしまい反発エネルギーには寄与しない、という考え方もできる。この場合は化学吸着量を同じにしてポテンシャルを比較しなければならないであろう。物理吸着樹脂が立体反発に寄与するかどうかは非常に難しい問題で、どのように扱うべきか明確な解答は出せないのが現状である。そこで今回は化学吸着樹脂のみが反発に寄与するという仮定に基づいて、吸着樹脂量が同じという条件で溶媒間の比較を行なうことにする。
シクロヘキサノンを溶媒として用いた場合と、酢酸2-エトキシエチルを用いた場合のポテンシャル曲線を比較したのがFig.33である。
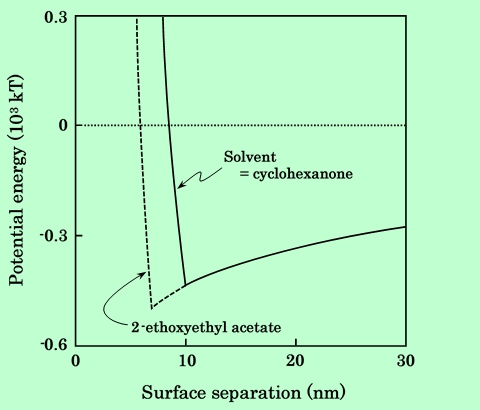
Fig.33 Effect of solvent on potential energy between parallel aligned
acicular particles.
第2章で解析したように、酢酸2-エトキシエチル中では吸着樹脂は比較的縮んだ状態になっており、吸着層中の樹脂濃度が高い。吸着層中の樹脂濃度は酢酸2-エトキシエチル中では約30%、シクロヘキサノン中では約20%である。従って、同じ吸着量で比較するとシクロヘキサノン中の方が約1.5倍、吸着膜厚が大きいことになる。そのため図に示すように2次極小の位置に差が生じ、シクロヘキサノンを用いた方が分散安定性が高いという結果になる。この結果は定性的には実験事実と一致しているが、現実には溶媒に関する現象はさらに複雑であることが予想され、定量的な考察のためには、樹脂の溶解性や粒子/溶媒、吸着層/溶媒界面の問題などについての詳細な検討を要すると思われる。
4.8 凝集体への粒子の付加
これまでは2個の粒子間のポテンシャルについてのみ検討してきたが、実際に粒子の凝集体が形成される際には、凝集体に対する1個の粒子の付加や、凝集体間の相互作用も重要であろう。しかし現実的には、粒子が不規則に集合した凝集体を定量的に扱うのは容易ではない。特に球形粒子と違って、針状や板状という等方的でない粒子の場合は粒子の向きに関する情報も与えてやる必要があり、凝集のシミュレーションは極めて困難である。そこで、極端に簡略化した凝集体モデルを用いて、そこに1個の粒子が1方向から付加するときのエネルギー変化を計算してみた。計算に用いたモデルをFig.34に示す。針状粒子の場合は、磁気モーメントの向きを互い違いにして筏状に凝集した塊に対して、その凝集面と同じ平面内で新たに1粒子が接近するものとする。また板状粒子では、磁気モーメントの向きを揃えて板面を平行にして積み重なった、いわゆるスタッキング型の凝集体に対して1個の粒子が重なって行くと考える。
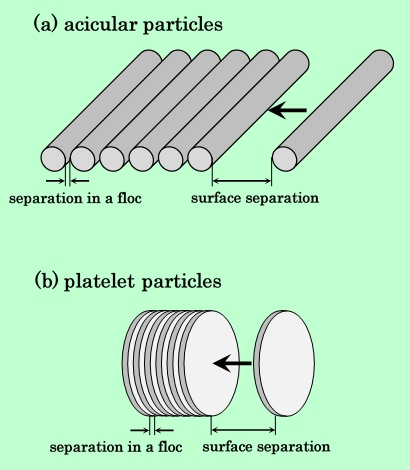
Fig.34 Schematic models of addition of one particle to a floc.
これらのモデルに基づいてポテンシャルを計算したのがFig.35、およびFig.36である。いずれの場合も凝集体内部での粒子間距離はゼロ、即ち粒子は互いに密着していると仮定し、凝集体中の粒子数を変化させて計算した。
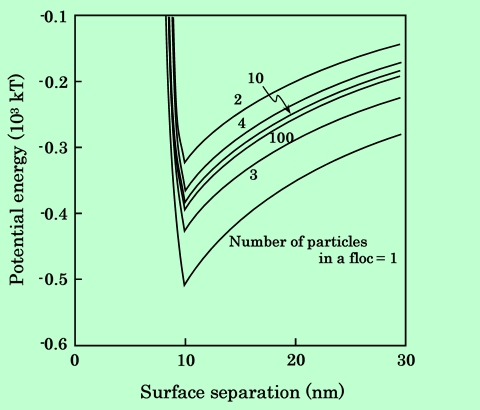
Fig.35 Interaction energy between an acicular particle and a raft-shape floc
shown in Fig.34. Number of particles in the floc are shown in the figure.
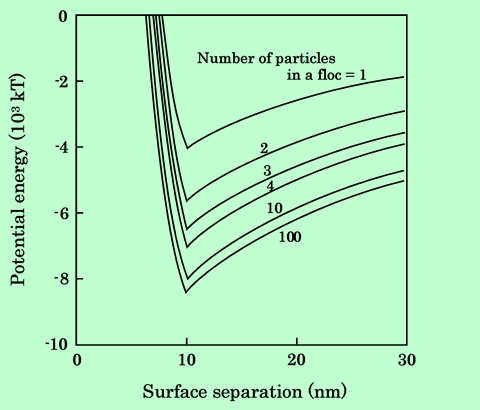
Fig.36 Interaction energy between a platelet particle and a stacking shown
in Fig.34. Number of particles in the floc are shown in the figure.
針状粒子の場合、凝集体中の粒子数が奇数のときに引力ポテンシャルが大きく、偶数のとき小さくなっている。これは、逆方向を向いた粒子の磁気モーメントが互いの磁場を打ち消し合うためで、当然の結果と言える。一方板状粒子では、磁気モーメントの向きがすべて同じであるので、粒子数が多くなるにしたがって引力エネルギーは単調に増加する。この点を明確にするために、2次極小の値を凝集体中の粒子数に対してプロットしたのが、Fig.37、Fig.38である。針状粒子の場合、2次極小値(の絶対値)は1対1の凝集の時が最も大きく、その後振動しながら一定値に収束して行くのに対し、板状粒子では単調に増加することが示されている。これらの結果から、針状粒子は大きな凝集体を作るよりも小さな凝集体を多数作った方がエネルギー的に有利であり、板状粒子は逆に連続した大きなスタッキング型凝集を起こした方が有利になるということが結論できる。
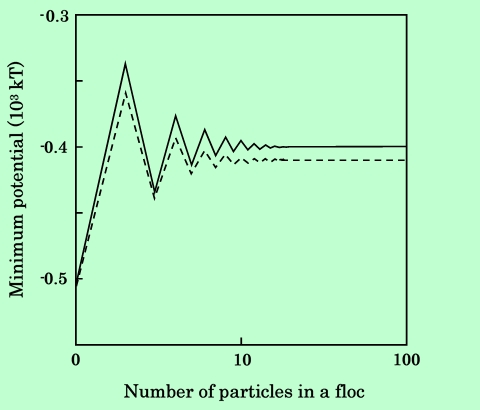
Fig.37 Dependence of minimum potential energy between an acicular particle
and a floc on the number of particles in the floc.
Solid line : Separation in the floc = 0 (Particles are contact each other).
Broken line : Separeation in the floc = 10 nm.
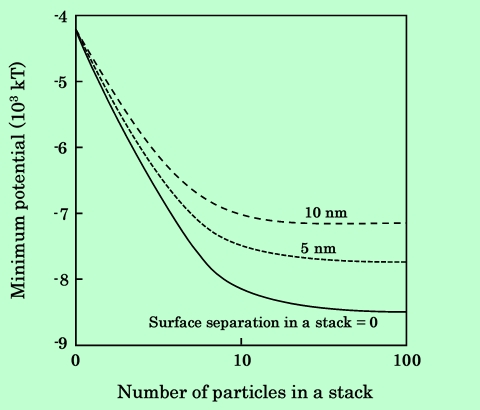
Fig.38 Dependence of minimum potential energy between an platelet particle
and a stack on the number of particles in the stack. Surface separation
in the stack are shown in the figure.
Fig.37、Fig.38には、凝集体を構成する粒子どうしが一定距離で隔てられている場合の計算結果も示している。針状粒子では粒子間を隔てることの効果はほとんど現れず、むしろ極小が深くなっているのに対し、板状粒子ではかなり大きく引力エネルギーが減少することがわかる。
実際に第1章で述べたような手法で粒子表面に樹脂吸着層を形成すれば粒子を数nm隔てることは可能であり、特に板状粒子に対しては凝集体の成長を抑制する効果が期待できるであろう。現実の凝集現象はこれほど単純ではないと思われるが、これらの計算結果は磁性粒子の分散・凝集の一つの特徴を表しているものと考えられる。
5. 結 言
分散液中における磁性粒子の粒子間相互作用を、磁気的引力、van der Waals引力、および表面の樹脂吸着層による立体反発力に分けて理論的に計算し、粒子の分散・凝集現象を解析した。磁気的引力エネルギーの計算では、粒子を200個程度のセルに分割して各セルの中心に置いた双極子の影響を積算する方法を採れば、充分な計算精度が得られることがわかった。van der Waalsエネルギーは、粒子を5層の板状片に分割して平板間の相互作用を求める式によって計算した。また樹脂吸着層による立体反発エネルギーの計算では、Bagchiの混合機構に基づく表式を針状および板状粒子に適用できるように拡張して用いた。
磁気的引力の計算からは、磁性粒子は双極子モーメントを同じ方向に向けて一列に配列した方が安定になることが示される。板状粒子では明らかにこの型の凝集が中心になる。しかし針状粒子では、双極子モーメントを逆平行にして配列した場合とのエネルギー差はほとんどなく、撹拌等の機械的な分散操作の影響も考慮して、逆平行型の凝集が主になるのではないかと推察された。このような磁性粒子の凝集形態については、分散液のTEM観察によっても、ある程度確認することができた。
2個の粒子の間の全相互作用エネルギーを粒子間距離に対してプロットした、いわゆるポテンシャル曲線には、ごく近距離に1次の極小、その外に極大、さらに外側に2次の極小が現れる。反発の極大値は数千kTになることが多く、これを乗り越えて粒子が接近することはほとんど不可能であるので、粒子の凝集は2次極小の所で起こると推定された。2次極小値に注目して種々の条件における磁性粒子の凝集性を検討したところ、粒子サイズ、吸着層膜厚、磁化量、樹脂分子量、溶媒の種類などの影響に関して、実験事実を半定量的に説明することができた。また、1個の粒子が新たに凝集体に付加する時のエネルギー計算から、針状粒子が小さい凝集体を多数作る傾向が強いのに対して、板状粒子は小数の大きな凝集体を形成した方がエネルギー的に有利である、ということが示された。
文 献
1)M.J.Vold, J. Colloid Sci., 16, 1 (1961)
2)E.J.W.Verwey, J.Th.G.Overbeek, "Theory of the stability of Lyophobic Colloids", Elsevier, Amsterdam (1948)
3)J.Lyklema, Adv. Colloid Interface Sci., 2, 67 (1968)
4)川口正美, 高橋 彰, 表面, 25, 601 (1987)
5)E.L.Mackor J. Colloid Sci., 6, 492 (1951)
6)E.L.Mackor and J.H.van der Waals, J. Colloid Sci., 7, 535 (1952)
7)E.J.Clayfield and E.C.Lumb, J. Colloid Interface Sci., 22, 269(1966)
8)E.W.Fischer, Kolloid Z, 160, 120 (1958)
9)R.H.Ottewill and T.Walker, J. Chem. Soc. Faraday Trans.I, 70, 917 (1974)
10)D.J.Meier, J. Phys. Chem., 71, 1861(1967)
11)F.Th.Hesselink, A.Vrij and J.Th.G.Overbeek, J. Phys. Chem., 75, 2094 (1971)
12)P.Bagchi, J. Colloid Interface Sci., 47, 86 (1974)
13)P.R.Gerber and M.A.Moore, Macromolecules, 10, 476(1977)
14)S.Levine, M.M.Thomlinson and K.Robinson, Diss. Faraday Soc., 65, 202 (1978)
15)J.M.H.M.Scheutjens and G.J.Fleer, Macromolecules, 18, 1882 (1985)
16)T.Sato, J. Appl. Polymer Sci., 23, 1693 (1979)
17)佐藤達雄, 表面, 18, 294 (1980)
18)D.H.Napper, J. Colloid Interface Sci., 29, 168 (1969)
19)J.N.Israelachivili and G.E.Adams, J. Chem. Soc. Faraday Trans.I, 74, 975 (1978)
20)P.F.Luckham and J.Klein, J. Chem. Soc. Faraday Trans.I, 80, 865 (1984)
21)P.C.Scholten, "Thermomechanics of Magnetic Fluids", p1, B.Berkovsky, Hemisphere, Washington
22)P.C.Scholten, J. Magn. Magn. Mater., 39, 99 (1983)
23)M.Ozaki, T.Egami, N.Sugiyama, E.Matijevic, J. Colloid Interface Sci., 126, 212 (1988)
24)I.Okada, M.Ozaki and E.Matijevic, J. Colloid Interface Sci., 142, 251 (1991)
25)D.Y.C.Chan, D.Henderson, J.Barojas, A.Homola, IBM J. Res.Develop, 29, 11 (1985)
26)H.Inoue, H.Fukke and M.Katsumoto, IEEE Trans. Magn., 26, 75 (1990)
27)H.Inoue, N.Kodama and M.Katsumoto, J. Magn. Magn. Mater., 124, 213 (1993)
28)P.J.Flory, J. Chem. Phys., 10, 51 (1942)
29)M.L.Huggins, J. Phys. Chem., 46, 151 (1942)
30)原崎勇次, "コーティングの基礎科学", 槙書店 (1977)
31)"化学便覧 基礎編", p100, 日本化学会 編, 丸善 (1984)
32)原田茂久, "磁気記録媒体総合資料集", p130, 松本光功 編, 総合電子出版社 (1985)
33)D.E.Speliotis, IEEE Trans. Magn., 26, 124 (1990)
34)R.Horimizu, H.Inoue, I.Matsuyama and M.Katsumoto, J. Magn. Magn. Mater.,114, 202 (1992)

Back
目 次
雑科学ホーム
hr-inoueホーム




















