
雑科学ホーム
hr-inoueホーム
● 熱の話 ●
とらえどころのない「熱」
その昔、物が燃えて熱を出す現象は「燃素(フロギストン)」という物質が出て行くことで説明されていました。燃える物には燃素が含まれていて、これが出て行くのが「燃焼」である、と考えたのです。ところが、金属が燃えると重くなることが示されるなど、燃素説ではうまく説明できない現象がいろいろと出て来て否定されて行きます。その後、「熱」の元は「熱素(カロリック)」という物質だとする説が出て来ました。熱素を多く持つほど温度は高くなり、熱素が移動することで熱が伝わって行く、と考えたのです。この説の支持者には、ラボアジェを初めとして科学史に名を残す錚々たる面々が名を連ねています。しかし、物を擦ればいくらでも摩擦熱が出て来ることや、熱が全く形の異なる仕事に変わることなどがわかって来て、熱素説は分が悪くなって行きます。今では、熱の正体が原子や分子の運動であることがわかっていますが、ここに至るまでには、様々な紆余曲折があったわけです。裏を返せば、とらえどころのない「熱」というものに対して、それだけ多くの関心が寄せられていた証拠でもあるのでしょう。
原子や分子の運動などを考える前から、熱や温度に関してはいろいろなことが調べられていました。原子・分子のミクロな話とは別に、気体の体積だとか圧力だとかの関係が、マクロなスケールで解釈されて行ったのです。これが「熱力学」と呼ばれるもので、本稿の主題になります。普通「熱力学」と言えば、微積分を駆使した、非常に数学的な色彩の濃い分野ですから(数学的には決して難しい部類ではないとは言え)、これを数式なしで説明することは、ムチャといえばムチャですが・・・・厳密さはちょっと横に置いておいて、また熱力学全体を網羅するようなことは初めから考えないで、ツマミ食い的に書いてみようと思います。また、熱を解釈する別のアプローチとして、原子や分子の集団的な挙動を統計的に扱う「統計力学」という分野もあります。「熱力学」と「統計力学」とは一緒に説明した方がわかりやすいことも多いのですが、この2つは元々考え方がかなり違いますから、個々の理論を理解する上では、かえって混乱を招くかもしれません。そこで、ここでは主に「熱力学」で話を進め、「統計力学」の考え方は、その都度、注釈的に付け加えることにしました。両者の目の付けどころの違いに注意してみてください。
熱はエネルギーの移動
ある物体が「熱」を持っているかどうかを知ることはできるでしょうか? そもそも「熱を持つ」とは、どういうことでしょう? 触ってみて熱ければ熱がある? それは単に「温度」が高いということでは? ならば「温度」とはいったい何でしょうか? まさに「?」の連発ですね。昔の人が解釈に苦労して、燃素や熱素をひねり出したのもわかります。原子や分子の運動を考えないで、「熱」を理解する方法はないものでしょうか。
ちょっと国語辞典を引いてみましょう。
― 熱とは、エネルギーの一種で、物体の温度を高めるもの ―
もう少し感覚的なことが書いてあるかと思いきや、意外に科学的に正確な記述になっていました(辞書に謝らないと・・・)。どうやら熱というのは、物体を温めることができるエネルギーである、ということらしい・・・。ここで、「温度の高い物体が持っているエネルギー」ではなくて、「物体の温度を高めるエネルギー」と言っているところがミソです。普通の感覚では、「温度が高い物体はたくさん熱を持っている」、と言いたいところですが、敢えて「他の物体の温度を高める」という表現になっているのです。つまり熱というのは、温度が高い物体が持っているエネルギーそのものではなくて、それが別のものに移動した時に初めて見えて来るものだ、ということです。
例えばここに熱湯があるとしましょう。いかにも熱そうで、いっぱいエネルギーを持っていそうです。でも、そのエネルギー自体は、今のところ目に見える形にはなっていません。「熱いのだからエネルギーを持っていそう」というだけで、実際にどれくらいの能力があるのかは、何らかの形で取り出してみないことには何とも言えません。そこで、この中にレトルトカレーのパックを入れてみます。冷たかったパックが温かくなりました。エネルギーが湯からパックに移動したのですね。この移動した分が、物理的な意味での「熱(エネルギー)」なのです。
「それならば、初めから熱を持っていた、ということでいいではないか!」、という声が聞こえてきそうです。それでは、こんな例はどうでしょう。少し空気を入れて先端を塞いだ注射器を、先ほどの熱湯に浸します。中の空気は温められて膨張し、ピストンを外へ押し出すでしょう。この場合、湯から注射器(の中の空気)に移動したエネルギーが熱であるわけですが、それが全て注射器を温めるのに使われたかというと、そうではありません。ピストンを押し出すということは、圧力という力をかけてピストンを動かしたわけですから、仕事をしたことになります(ここで言う仕事はもちろん、働いて給料をもらう類の仕事ではなく、力を働かせてその方向に物を移動させる、あの物理学的な仕事のことです)。仕事もエネルギーですから、注入された熱の一部は、熱ではない、別のエネルギーに変わったことになります。それでは、注射器を温めた方のエネルギーは何と呼べばいいでしょうか。熱から仕事に変わった分を差し引いた残りだから、「熱の残り」と言ってもいいのですが、熱とは別の「見えないエネルギー」として注射器に蓄えられた、と考えることもできますね。
そこで、「熱」という名前は、ある物から別の物に移動する部分だけに使うことにして、温かさとして蓄えられているエネルギーは違う名前で呼ぶことにします。これが内部エネルギーです。そうすると、初めの熱湯が持っていた得体の知れないエネルギーも、内部エネルギーであったことになります。つまり、熱湯が持っていた内部エネルギーの一部が熱として注射器に移動し、その一部が注射器の内部エネルギーとして蓄えられ、残りの部分がピストンを押す仕事に変わった、と考えられるのです。この様子を表したのが図1です。残念ながら内部エネルギーそのものを直接に計ることはできません。しかし、熱や仕事として移動する様子を調べれば、図1のような単純な構図が見えて来るのです。
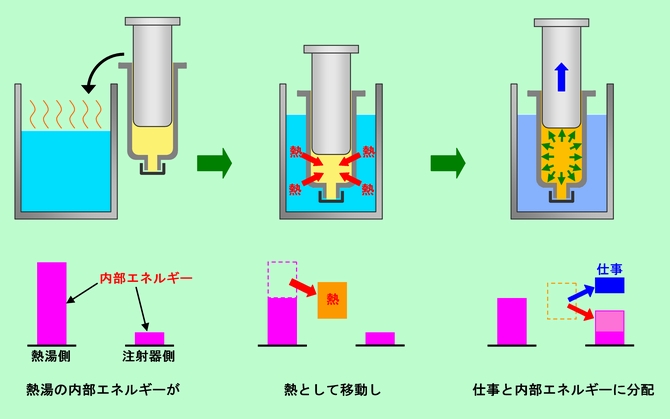
図1 内部エネルギーと熱と仕事
実は「仕事をする」というのもエネルギーを移動させることです。例えば、モーターを回して石を持ち上げる場合、モーターが仕事をすることで、電気エネルギーが石の位置エネルギーに移ることになります。このように機械的な働きでエネルギーが移動する時、そのエネルギーを「仕事」と呼び、それ以外の方法でエネルギーが移動する時に「熱」と呼ぶのです。その意味で、熱と仕事は親戚のようなもの、と言うことができます。
エネルギーは保存される(はず)
図1には、重要な法則が隠れています。注射器側が受け取った内部エネルギーと、ピストンがした仕事のエネルギーを足し合わせると、熱湯から移動した熱量にピッタリ一致するのです。これが「エネルギー保存の法則」で、「熱力学第一法則」とも呼ばれます。「いちいち法則だなどとエラそうに言わなくても、そんなのは当たり前だ」と言われそうですね。しかし、本当に当たり前なのでしょうか。
何もないところから突然にエネルギーが湧き出すことは、たぶんないでしょう。もしそんなことが起こったら、全くエネルギーを与えなくても永久に動き続ける永久機関が作れてしまいますし、エネルギー危機も起こらないでしょう。また、エネルギーは形を変えこそすれ、消えてなくなってしまうことはない、というのも、感覚的には理解できると思います。しかし、これを証明しろと言われたら・・・・・実は誰にもできません。本当にできないのです。ならばどうしてこれが法則として通るのか、と言えば、まず感覚的に矛盾がないから、そしてこれまでに一度たりともこれに反する事実が見つかっていないからなのです。何とも頼りない話ですね。しかし、そもそも熱力学というのは、このような経験則を基本に成り立っているものです。そこに文句をつけると熱力学自体が成り立たなくなってしまいますから、ここは百歩譲ってください(強引?)。
熱力学第一法則と言えば、普通は当然のように数式が出て来るところですが(たぶんその方がわかりやすいですから)、言葉で書くと、次のような感じでしょうか。いろいろな言い方ができますが、どれも結局は同じことを表しています。
(a) 「外から入って来た熱量」は、「内部エネルギーの増加」と「外に向かっての仕事」に分配される。
(b) 「内部エネルギー」は、「外から入って来た熱量」と「外からされた仕事」の分だけ「増加」する。
(c) 「外からされた仕事」は、「内部エネルギーの増加」と「外に出す熱量」に分配される。
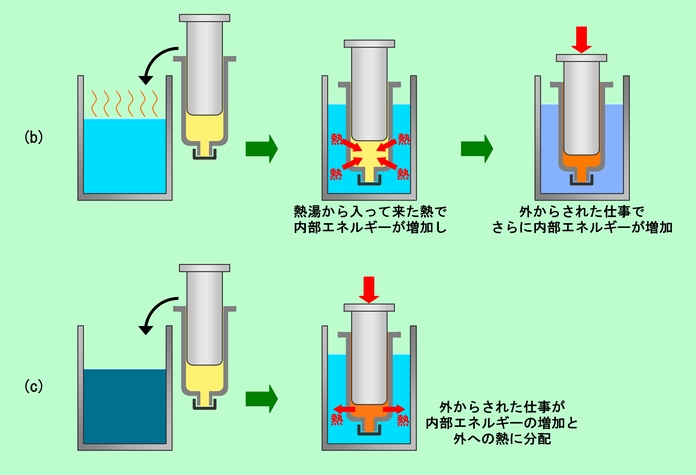
図2 内部エネルギーと熱と仕事 その2 (別のパターン)
(a)は図1の注射器の場合と同じです。(b)はどんな感じかと言うと、例えば図2(b)のように、空気の入った注射器を熱湯に入れて温めると同時に、ピストンをギュッと押し込んだ状態に相当します。この場合、熱湯から熱が入って来て温度が上がりますが、それに加えて空気が無理やり圧縮された(外から仕事をされた)ために、さらに温度が高くなります。つまり、注射器(の中の空気)の内部エネルギーは、ダブルで増えることになるのです。(c)はどうでしょうか。今度は図2(c)のように、注射器を水に入れて、ピストンを押し込んだ場合に相当します。空気が無理やり圧縮された(外から仕事をされた)ことで内部エネルギーが増える(温度が上がる)と同時に、仕事の一部が熱となって周囲の水に移るのです。
【補足】 統計力学では、内部エネルギーは原子や分子の運動のエネルギー(並進運動や振動など)として解釈されます。熱力学では全く気にしない「微視的」な視点が基本になるのです。もちろん個々の分子の運動状態はそれぞれ違うはずで、それを1個1個調べようとすれば、とんでもないことになってしまいます。しかし、多量の分子が集まった集団全体で考えれば、速度の平均値はこのくらいで、速度の分布はこんな形、といったことが「統計的に」求められるのです。そのため、「熱力学」では直接は測ることができなかった内部エネルギーも、統計力学では分子の運動状態から見積もることができます。
「熱」と「仕事」は、手順によって変化する
「内部エネルギー」と「熱」と「仕事」、この3つの収支が常に合わなければならない、ということはおよそ理解できたと思いますが、何か足りない気がしませんか? 例えば、先に挙げた(a)の場合ですが、外から入って来た熱のうち、どれだけが内部エネルギーになって、どれだけが仕事になるのか、ということがわかりません。分配の比率は、いったいどうなっているのでしょうか。実は、これが一筋縄では行かないのです。
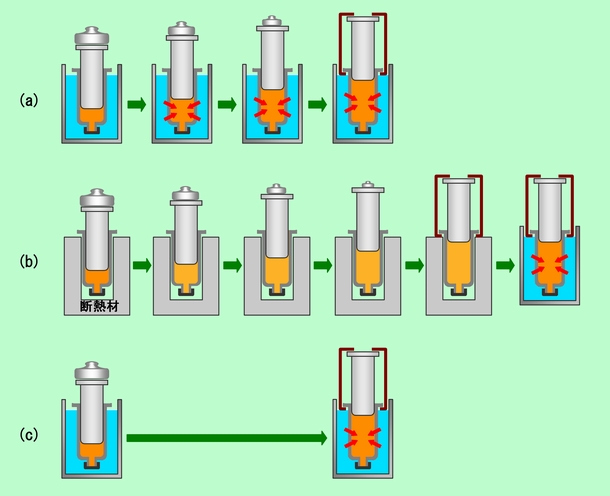
図3 違う方法で膨張させると・・・・
図3のようなケースを考えてみましょう。出発点は、熱い空気がオモリで押さえつけられている状態で、これを決められた体積まで膨張させて行きます(タガをはめて、ピストンが一定の高さまでしか上がらないようにしてあります)。(a)は、初めにピストンを押さえていたオモリを徐々に軽いものに換えて、少しずつ膨張させています(本当はもっと細かくオモリを交換したと思ってください)。膨張すると温度が下るのですが、すぐに湯から熱が供給されて、中の温度は常に一定に保たれています。これに対して(b)は、注射器を断熱材で包んで熱の出入りを完全に遮断した状態で膨張させています。熱が供給されませんから温度は下ってしまいますので、ピストンが決められた位置まで上がったところで温め直して元の温度に戻します。最後に(c)ですが、今度はいきなりオモリを外して一気に膨張させています。(a)と同じように熱は供給されるのですが、膨張の過程が大きく違っています。このように(a),(b),(c)の3つで、最初と最後の状態は全く同じなのですが、途中の過程が違っているわけです。
最初の状態が同じなのですから、初めに注射器の中の空気が持っていた内部エネルギーは(a)も(b)も(c)も同じ、と考えられます。また最後の状態も同じですから、最終的な内部エネルギーも同じはずです。ということは、注射器の中の空気が膨張した時の内部エネルギーの変化量は、(a)でも(b)でも(c)でも同じ、ということになります。当たり前ですね。それでは仕事はどうでしょうか。(a)と(b)では、常にオモリを持ち上げるだけの力を出しながら膨張しています。膨張するに従って圧力が下がるので、力はだんだん弱くはなりますが、最後まで、その時々の最大の力を発揮し続けているのです。ただし(b)では温度が低くなるので、 同じ体積の時の力は(a)よりも弱く、その分(a)よりも仕事は少なくなるはずです。最後に温めて圧力を戻す段階では、ピストンはもう動きませんから、どんなに力がかかっても仕事はゼロです。一方(c)では、外からピストンを押し返す力が急に弱くなりますので、本来はもっと強い力が出せるはずが、ほぼ空振り、という状態になります。重そうな荷物を力をこめて押したところ、意外に軽くてつんのめった、という感じで、言い方を変えれば、(a)や(b)と比べて楽に膨張した、ということです。この場合、ピストンを押す力が弱くて済むのですから、仕事は(a)や(b)よりも少ないことになります。
図3の3種類の膨張の様子を、「体積」を横軸、「ピストンを押す力」を縦軸にとってグラフにすると、図4のようになります。仕事は、力と移動距離との掛け算ですから、図の赤く着色した部分の面積が仕事量を表します。ピストンの最終的な移動距離が同じなので、仕事量はピストンを押す力で決まることになります。
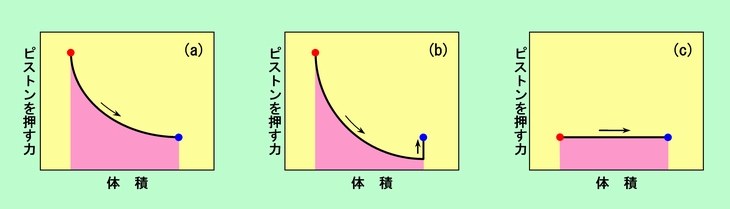
図4 最初と最後が同じでも仕事量は違う
オモリの交換をものすごくこまめにやれば、空気の圧力(=ピストンを押す力)は滑らかに減少するでしょう。その時の減少の仕方は、熱の供給がある(a)の方が、熱の供給のない(b)よりも小さくなります。その結果、力の強い(a)の方が仕事は大きくなることがわかります。(c)ではピストンを押す力(これは注射器内の空気の圧力とは違います)が初めから弱いので、仕事量はさらに少なくなるのです。
(実は(c)の場合には、急激な膨張のために温度も瞬間的には下がるでしょうし、注射器内の空気の圧力も実際にどうなっているかは厳密にはわかりません。つまり、普通の圧力と体積の関係を示すグラフ(状態図)は、(c)については描くことができません。ここでは縦軸に「ピストンを押す力」をとることで無理やりグラフ化しているのです。)
内部エネルギーの増え方が同じなのに仕事の量は違っている、ということになると、帳尻を合わせるには、熱の出入りが違って来なければなりません。つまり、湯からもらう熱量も違っていて、(a)>(b)>(c)の順になっている、ということです。
内部エネルギーのように、どういう手順を経ても、状態さえ決まればビシッと決まってしまう量のことを、熱力学では「状態量」と呼びます。体積や圧力や温度も、どんな手順で膨張させようが圧縮しようが、暖めようが冷やそうが、1リットルは1リットル、5気圧は5気圧、70℃は70℃ですから状態量です(だからこそ、体積や圧力を示すことでその状態を表すことができるのです)。これに対して、熱量や仕事量のように、どんな手順で変化させるかで結果が変わってしまう量は状態量ではありません。この点は非常に重要で、ここがあやふやになっていると頭がこんがらがって、熱力学が理解できなくなってしまう原因になります。
熱や仕事が状態量ではないということは、熱力学の理解だけでなく、現実的に非常に重要なことでもあります。なぜなら、もし熱や仕事が状態量だったら、蒸気機関のように熱エネルギーを使って繰り返し動力を生み出す装置が作れなくなってしまうからです。繰り返し動力を生むためには同じ動作を何回も繰り返さなければなりません。つまり、一回の動作で装置が元の状態に戻らなければなりません。この時に熱や仕事も一周回って差し引きゼロになってしまったのでは、そこから別のエネルギーを取り出すことなどできないのです。(このことは、後でまた出て来ます)
温度を決めるのは難しい
内部エネルギーは物が温かさとして蓄えているエネルギーですから、当然温度に関係しています。そして温度が高いほど内部エネルギーも大きくなる、ということは見当が付くでしょう。それでは、その温度はいったいどうやって決めたらいいのでしょうか。
触ってみて熱いか冷たいか、というのが一番原始的な決め方でしょうが、手の温度が高い人と低い人では感じ方が違って来ますし、数値で表すこともできません。そこで考えられたのが、たいていの物は熱くなると膨張し、冷たくなると収縮する、という性質があることを利用して、その膨張の度合いで温度を測る方法でした。基準点をどこにするかで値は変わりますが、最も一般的なのは、水の凝固点を0度、沸点を100度と決め、その間を100等分した摂氏温度でしょう。アルコールや水銀を使ったこの方式の温度計が作られ、これらが今でも便利に使われていることは、誰でもよく知っている通りです(現在アルコール温度計と呼ばれているものの中身は、実はアルコールではなく灯油の類です)。この流れで、面白い発見もありました。液体ではなく気体を使った温度計で、体積と温度の関係を調べたデータをずっと低温まで延長すると、マイナス273度で体積がゼロになるはずだということがわかったのです。体積がマイナスになることはないので、ここが温度の最低点だということになります。これが絶対零度の発見で、18世紀末から19世紀にかけてのことです。
物質の熱膨張を利用した温度計ができたことで温度を決める問題は解決したか、というと、そう簡単には行きません。熱膨張は常に温度にキッチリと比例するわけではありませんし、その動きは物質によって違います。そのため、厳密に言えば目盛は等間隔にはなりませんし、使う物質によって値がズレてしまう、ということが起こるのです。実際の例を見てみましょう。図5(a)は、いくつかの液体について、温度を上げるとどれくらい膨張するかを示したものです(0℃の時の体積を1としています)。このように膨張の仕方は物質によって大きく異なるので、使う物質によって目盛は全く違ってしまいます。また、このグラフが直線になってくれればまだいいのですが、図のようにたいていは下に凸のカーブを描きます。特に水の場合は、(図ではよくわかりませんが)一旦収縮して4℃で最小体積になった後に大きくカーブを描いて膨張しています。水銀も、図ではほとんど直線のように見えますが、これでも実際にはわずかにカーブしているのです。ですから、これらの液体を使って温度計を作り、0℃と100℃の間を等間隔に目盛ると、大きな誤差を生じてしまいます。
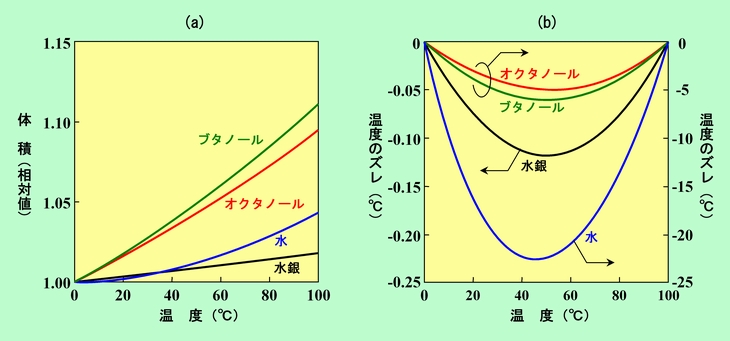
図5 液体の熱膨張を利用して温度計を作ると・・・・
その誤差を表したのが図5(b)です。横軸は実際の温度(まだ温度の定義ができていないのに「実際の温度」と言うのは少々気が引けますが)、縦軸は、温度計の表示温度と実際の温度のズレを示しています。水銀とその他の液体ではズレ量が大きく違うので、水銀は左の軸で、その他の液体は100倍スケールの右の軸で表しています。この図を見ると、最も誤差の小さい水銀でも、50℃付近では0.1℃以上の誤差があることがわかります。水にいたっては20℃以上、アルコールの一種であるオクタノールでも5℃ぐらいの誤差です。ですから、これらの液体で作った温度計で正しい温度を表示できるようにするには、高温になるほど目盛間隔を広くしなければなりません。0℃付近と比べて100℃付近では、水銀温度計ならば1%ぐらい、オクタノール温度計ならば50%近くも目盛間隔を広げる必要があるのです。精度の高い温度計では、実際にこのような目盛付けがされています。水銀温度計では目盛間隔の違いが小さくてわかりにくいですが、よく目にする赤い液の入ったアルコール温度計 (前記のように、中身はアルコールではなくて灯油)ならば、高温領域の目盛がかなり広くなっているのがわかると思います。(表示温度をいくつかの区間に分けて、区間ごとに目盛の幅を変えている場合もあります。この方式ですと区間内は等間隔なので、そこで誤差が出ます)。
こうなって来ると、日常生活はともかくとして、やはり科学の世界では、使う物質によらない、もっと普遍的な温度の尺度が必要ですね。そこで登場するのが、熱機関です。熱機関というのは熱を動力に変える装置のことで、水を加熱して高圧の蒸気を作り、その圧力を使ってピストンを動かす蒸気機関や、羽根車を回す蒸気タービン、ガソリンを燃やした熱で高圧ガスを作ってピストンを動かすガソリンエンジンなどは、全て熱機関の一種です。これが温度とどう関係するのか、ということですが、温度の話にたどり着くには少々長い前段が必要ですのでしばらくガマンしてもらって、熱機関について大まかに見てみましょう。
熱を仕事に変える装置 ― 熱機関 ―
まず、実際の熱機関はかなり複雑なので、もっと単純な例を考えましょう。水を蒸気に変えたり、ガソリンを燃やしたりするのは、化学変化や液体・気体の変化が起こって面倒ですから、気体だけの膨張や収縮を使うことにして、図6のような仕組みを作ってみます。
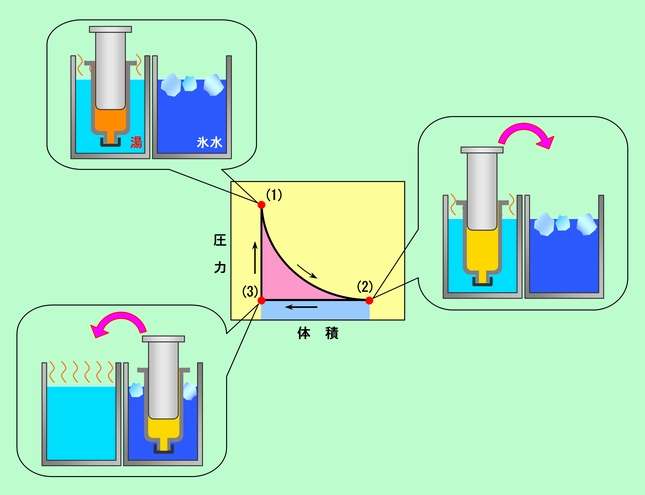
図6 熱機関の例
どこから出発してもいいのですが、例えば、注射器を湯に浸して中の圧力が上がった状態の(1)から始めましょう。(1)では、中の空気の温度は湯と同じで、圧力は外の気圧よりも高いですから、膨張してピストンを押し上げ(もちろん、圧力は徐々に下って)、(2)の状態に移って行きます。この時、空気は外に向かって仕事をしていて(図3のようにオモリを持ち上げるような動作を考えてください)、その大きさはグラフの曲線の下の部分の面積に相当します。湯からもらった熱を仕事に変えているわけです。行き着いた(2)の状態では、温度は湯と同じままですが、圧力は(ピストンの重さを無視すれば)大気圧と同じになっているでしょう。次に、注射器を氷水に移して冷やします。すると温度が下がって空気が収縮し、(3)の状態になります。温度は氷水と同じ、圧力は最初から最後まで一定で、大気圧と同じです。この過程では、空気は圧縮されていますから、外から仕事をされています。その量は、図の薄い青に色付けした部分に相当します。ここでは、外からされた仕事の分だけ、熱を氷水に捨てているのです(実際には仕事分以上に熱を捨てて内部エネルギーも減らしているのですが、減った内部エネルギーは(3)→(1)の過程で取り返すので、差し引きゼロです)。最後に、ピストンを固定した状態で注射器を再び湯に入れて温め、(1)の状態に戻します。ピストンが動いていないので、この過程での仕事はゼロです(吸収した熱は全て内部エネルギーとして蓄えられます)。以上で、一回のサイクルが完結しました。注射器の状態は完全に元に復帰し、何度でも同じサイクルを繰り返すことができます。
このサイクルで取り出すことができる仕事は、というと、(1)→(2)で外に向かってした仕事と、(2)→(3)で外からされた仕事の差、ということになります。ちょうど図6のグラフの赤で色付けした部分です。そしてその仕事は、湯から受け取った熱と、氷水に捨てた熱の差になっているのです。
前にも書きましたが、このように熱機関のサイクルで仕事を取り出せるのは、熱と仕事が状態量ではないからです。(1)→(2)の行きの過程と、(2)→(3)→(1)の帰りの過程で、出入りした熱量が違っていて、その差が仕事に化けているのです。もし熱が状態量だったら、一回りすると完全に元の状態に戻ってしまいますから、出入りの差し引きはゼロになるはずで、そうなると仕事は取り出しようがない、というわけです。くどいようですがもう一度・・・・熱と仕事は状態量ではありません。
「準静的」という超現実的な過程
図6に示したようなサイクルは、熱力学の教科書では普通は出て来ません。なぜかと言うと、途中途中で注射器の内と外で温度が違っていて、熱的に落ち着いた状態になっていないからです。内と外で温度差があると、熱は温度の高い方から低い方に流れ込みます。最終的には同じ温度になったところで落ち着くわけですが、そこに至る過程では、温度や圧力がどのように変化して行ったかをキチンと追跡することができませんし、逆方向に戻して行くこともできないのです。
そこで理想的な熱機関を作るために、内と外の温度や圧力がいつも同じになっている状態を考えます。これが平衡状態です。内外の状態が同じですから、熱はどちら向きにも同じように移動できますし、注射器のピストンもどちら方向にも移動可能です。要するに「平衡状態」というのは、どちら向きの変化も同じように起こり得る状態、ということです。そして、この平衡状態だけで、膨張や圧縮の過程を考えて行こう、というのです。
しかし、ちょっと待てよ・・・・。いつも平衡状態にあるのなら、熱の出入りもピストンの移動も起きないはず。ということは、温度の変化も膨張も圧縮も起きないのではないか・・・・。確かにその通りです。そこで、さらに超人的なことを考えます。例えば、平衡状態から外の温度をちょっとだけ上げたとします。すると外から内に熱が流れ込み、すぐに新しい平衡に達します。これを繰り返せば、いずれは何度でも何十度でも、全体の温度を上げることができますね。この「ちょっとだけ温度を上げる」幅を無限に小さくすれば、常に平衡状態を保ちながら温度を上げることができるはず、と考えるのです。膨張や圧縮も同じで、変化を無限に小さくすれば、平衡状態を壊すことなしに状態を変えることができるでしょう。常に平衡の状態にありながら、状態変化は自由にできる・・・・・すごいワザですね。もちろん、これを実際にやろうとすれば、ものすごく長い時間がかかることは容易に想像できるでしょう。何せ「無限に遅く」動かすのですから。しかし、頭で考えるのは自由です。これが、熱力学でよく出て来る「準静的過程」というヤツです。「動く」のだけれど、「止まっている状態の延長」、と考えるわけです。実はこの考え方は、図3で既に出て来ています。図3(a)や(b)のオモリを徐々に軽いものに換えて行く操作で、オモリの重さの刻み幅を無限に小さくすれば、これが準静的な膨張になるのです。
温度差や圧力差がある時は、準静的過程にはなりません。温度差があると、温度の高い方から低い方への熱の移動が逆方向よりも多くなりますから、外から見ると熱が一方的に高温部から低温部に流れ込むように見えます。変化が、双方向ではなく一方向になるのです。そしてその逆の流れが自然に起こることはありません。いつの間にかぬるま湯の一部が沸騰し、別の部分が凍ってしまった、ということは自然には起きないのです。同様に圧力差がある時も、高圧部から低圧部へ向かう一方的な流れが起こります。図3(c)はその例で、内側の圧力の方が高いために注射器内の空気は一方的に膨張するのみで、途中で逆方向に進む余地は全くありません。外から何らかの操作を加えない限り、低圧部から高圧部への流れが起こることはないのです。
(「準静的過程」とよく似た言葉に「可逆過程」というのがあります。「準静的過程」は常に平衡状態を保っていて、平衡状態というのはどちら向きの変化も同じように起こる状態なのですから、「準静的」なら常に逆方向への変化も可能、つまり「可逆」ということになります。逆に「可逆」、即ち常に逆方向にも行ける状態で変化させるということは、いつも平衡状態を保っている、ということですから、「準静的」ということになります。要するに、「準静的過程」と「可逆過程」は同じと考えてよい、ということです。「準静的」の解釈を拡げると、膨張する時にピストンと壁の間に摩擦があるとか、ぶつかって音が出たとか、いろいろややこしい条件を持ち込んで、「準静的」であっても「可逆」ではない過程を考えることはできます。しかし、ここまで理想化した状況を考えているのに、摩擦や音を持ち出すのは、どう見てもバランスが悪いですから、ここでは「準静的過程」と「可逆過程」は同じ意味で使います。「準静的」でない過程はもちろん、自然に逆方向に進むことのない「不可逆過程」ということになります。)
それでは準静的過程(可逆過程)だけを使って、できるだけ簡単な熱機関のサイクルを作ってみましょう。有名なカルノーサイクルです。
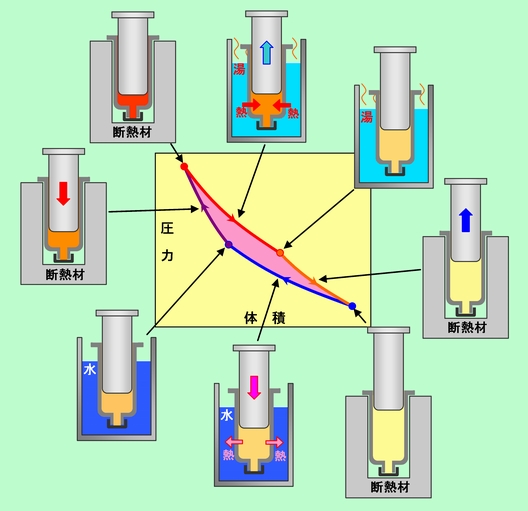
図7 可逆熱機関の代表 ― カルノーサイクル ―
出発は左上の赤丸で、体積が小さく、温度と圧力が高くなった状態で、ここから時計回りにサイクルを動かして行きます。まず、中の空気と同じ温度の湯を用意し、この中で常に湯と同じ温度を保ちながら、ゆっくりゆっくり膨張させます(図の赤線=等温膨張)。膨張の仕事で使ったエネルギーを、すぐに湯からの熱で取り戻すわけで、内部エネルギーは全く変化しません(湯はたっぷりあって、温度変化が無視できるとします)。次に、温度一定で膨張した空気を冷やさなければならないのですが、ここでいきなり氷水に浸したりすると、温度差ができてしまって可逆過程になりません。かといって、ちょっとずつ温度の違う湯(水)を無限個用意して順番に浸して行く、というのも面倒すぎます。そこで、湯との関係を一度断ち切って、例えば注射器を断熱材で包むなどして熱の出入りを一切なくした状態で、さらに膨張を続けます。いわゆる断熱膨張です(橙線)。この時にも、外からピストンを押す力を中の空気の圧力よりもほんのちょっとだけ小さくしながら、無限にゆっくりと膨張させなければなりません。ここでも空気は膨張することで仕事をしますが、今度は外からの熱ではなくて、空気が持っている内部エネルギーを使って仕事をするので、空気の温度は下って行くことになります。
温度が十分に下がったところで、今度は同じ温度の水に注射器を移します。そしてまた、同じ温度を保ちながらゆっくりゆっくり圧縮して行きます(青線=等温圧縮)。圧縮という外からの仕事で得たエネルギーを、熱という形で外に出して行くわけです。最後に、また注射器を断熱材で包んで熱の出入りを遮断し、断熱圧縮します(紫線)。外からの仕事は熱になって出て行くことができないので、全て内部エネルギーとして蓄えられます。その結果、空気の温度が上がって、元の状態に戻るのです。
結局カルノーサイクルでは、高温の湯から熱をもらってピストンを押し出す仕事をし、低温の水に熱を放出することでピストンを戻して(つまり外から仕事をされて)元の状態に復帰するのです。その時、高温でする仕事の方が低温でされる仕事よりも大きいので、図で赤く色付けした部分の面積に相当する正味の仕事を取り出すことができる、ということです。途中の2度の断熱過程は、湯と水という2つの温度の間を可逆的につなぐ役割を果たしていると言えます。
カルノーサイクルを初めとする可逆機関は「可逆」なのですから、当然ながら逆向きの運転もできます。図7の過程を左回りに進めれば、外から余分な仕事を供給することで、低温の水から高温の湯に熱を移すことができるのです。これがエアコンや冷蔵庫に使われるヒートポンプの基本的な原理です(実際のヒートポンプは少し方式が違いますが)。まさに、熱を低いところ(低温熱源)から高いところ(高温熱源)に、ポンプのように汲み上げているわけですね。
ところで、可逆機関を動かすには、図7の湯と水に相当する2つの熱源を準備する必要があります。一方から熱を取り出し、もう一方に熱を捨てることで元の状態に復帰するわけで、片方だけではサイクルを完成させることはできません。もしも熱源が1つで済むのであれば、身の回りの空気や海水などが持っている熱を、別の形で全部取り出すことができてしまいますが、このような熱機関は長い歴史の中でいっさい見つかっておらず、実現不可能である、ということが経験的に知られています。これが「熱力学第二法則」です(その他にもいろいろな表現がされていますが、どれも同じことを言っています)。
【補足】 第一法則に続いてまた「経験則」か、という感じですが、そもそも「熱が高温部から低温部に流れる」とか、「高圧部から低圧部に気体が流れる」という元々の前提自体も経験的なものです。熱力学というのはそういうもの、ということで、ここも百歩譲ってもらいましょう。統計力学を使うと、分子の微視的な運動の観点から、ある程度は理屈で説明することも可能です。しかし、完全に理論的に第二法則を導く、ということに関しては、まだ決定打はないようです。
可逆機関で温度を決める
共通の熱源の間で動く2つの熱機関を組み合わせると、いろいろと面白い性質が見えて来ます。ちょっとパズルのような感じですから、頭を柔らかくして、図8を見てください。
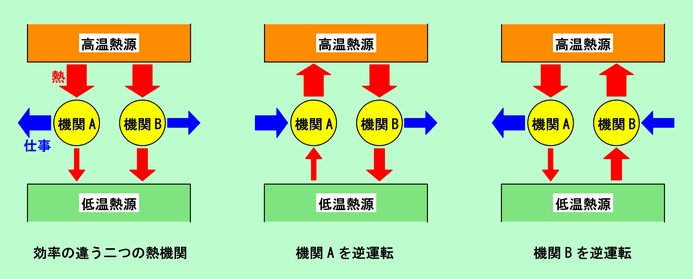
図8 熱機関を組み合わせると・・・・
まず左端の図ですが、ここでは機関Aと機関Bは共に、高温熱源から熱をもらって仕事をし、残りの熱を低温熱源に放出しています。高温熱源からもらう熱はどちらも同じですが、Aの方が低温熱源に捨てる熱が少なく、その分多くの仕事ができる、つまり効率のよい機関です。ここで機関Aが可逆機関であるとすると、逆運転ができますから、中央の図のような組み合わせが可能です。ここでは機関Aは低温熱源から熱を吸収し、仕事を投入して、多量の熱を高温熱源に返しています。この図を全体として眺めてみてください。高温熱源はBに熱を供給し、同じ量の熱をAから返してもらっていますから、何も変化はありません。一方、低温熱源の方は、Aに与えた熱よりもBからもらった熱の方が多いですから、トータルとして、熱量が増えています。その増えた熱はどこから来たかというと、言うまでもなく、Aに投入された仕事とBがした仕事との差からです。つまり、全体として余分な仕事をもらい、それを熱として低温熱源に放出したわけです。仕事が熱に変わっただけですから、何の問題もありません。
さて、ここからが問題です。今度は機関Bが可逆であるとして、こちらを逆運転してみましょう。その様子を示したのが右端の図です。高温熱源のトータルの熱の出入りはやはりゼロですが、低温熱源の方は、Aからもらった熱よりもBに与えた熱が多いので、トータルとしては熱を吸い取られています。そして、Bに投入した仕事よりもAがした仕事の方が多いので、全体としては外に向かって仕事をしたことになります。つまり、低温熱源から一方的に熱をもらい、どこにも熱を捨てることなく仕事に変えたことになるのです。これは明らかに熱力学第二法則に反していますから、実際にはあり得ません。以上のことから、効率の違う二つの熱機関があった場合、効率の悪い方は可逆機関ではあり得ない、言い換えれば、最も効率の良い熱機関は可逆機関である、ということになります。
また、こんな見方もできます。もし機関Aも機関Bも可逆機関であったとすると、Bを逆運転した時に先のような矛盾が起こります。ということは、AもBも可逆機関であるためには、図8のように効率に差があってはいけない、ということを意味しています。つまり熱源の温度が決まっている場合には、可逆機関は全て同じ効率でなければならないのです。
ここまで来てようやく、温度に関する重要な法則が出て来ました。可逆機関の効率は熱源の温度だけで決まる、ということです。それならば・・・・逆に可逆機関の効率を基にして、温度計の種類に依らない絶対的な温度を新しく定義してやればよい、という発想が出て来ます。可逆機関が高温熱源からもらう熱量と低温熱源に捨てる熱量の比が熱源の温度だけで決まるのですから、熱量の比をそのまま2つの熱源の絶対温度の比、としてやるのです。これが「熱力学的温度」と呼ばれるものです。
絶対温度の原点は初めから決まっています。低温熱源に捨てる熱がゼロになる極限の状態(この時、高温熱源から吸収した熱は全て仕事に変わるので、効率は100%)の温度が絶対零度です。あとはもう一ヶ所、基準温度を決める必要がありますが、それまで使われていた(というか今も使われている)摂氏温度とほぼ一致するようにした方が便利ですから、水の凝固点を273.15度にすることに決められました。このようにすると、水の凝固点と沸点の温度差がちょうど100度になって、摂氏温度がほぼそのまま絶対温度の代用として使えます。その後、基準の決め方や温度の定義の仕方に関してはいろいろと変遷がありましたが、元々熱力学を基にした温度というのはこういうものなのです。
(細かいことを言うと、理想的な可逆機関を実際に作ることはできないので(近いものはできますが)、絶対温度の決定には少々テクニックを要します。大雑把に言うと、何らかの現象に関して、温度計で測った温度(実用温度)と絶対温度の両方を含んだ式を理論的に導き出し、その中に含まれる測定可能な数値を実際に求めることで、実用温度を絶対温度に関係付ける、ということです。)
エントロピー登場
可逆機関では、一方の熱源とやり取りした熱量と、もう一方の熱源とやり取りした熱量の比が、熱源の絶対温度の比になっていました(そうなるように絶対温度を定義したのですから当然ですが)。つまり熱源の温度が高いほど、そことやり取りする熱量も多くなるわけで、別の言い方をすれば、熱量と絶対温度の比が常に一定になる、ということでもあります。もちろん、熱機関ごとに比の値そのものは異なりますが(例えば、規模の大きな熱機関を使えば、やり取りする熱量は当然大きくなります)、同じ可逆熱機関を運転している限りは、熱量を絶対温度で割った値はいつも同じなのです。そこで、この熱量を絶対温度で割った値を新たな量Sと呼ぶことにしましょう。すると、一方の熱源から熱をもらう時にSが増え、もう一方の熱源に熱を捨てる時にSが同じだけ減るので、可逆機関を一回りさせた時のSの変化は差し引きゼロになることがわかります。図7のカルノーサイクルならば、赤線の等温膨張の過程でSが増え、青線の等温圧縮の過程で同じだけSが減るのです(橙線と紫線の部分は断熱過程で熱の出入りがないので、Sの変化はありません)。熱量は赤線と青線で違うのに、Sは同じ・・・・何か面白い性質がありそうです。このSについて、もう少し詳しく見てみましょう。
図7は1個のカルノーサイクルだけの話なので、特殊なケースかもしれません。そこで図9のように、複数のカルノーサイクルを組み合わせることを考えます。
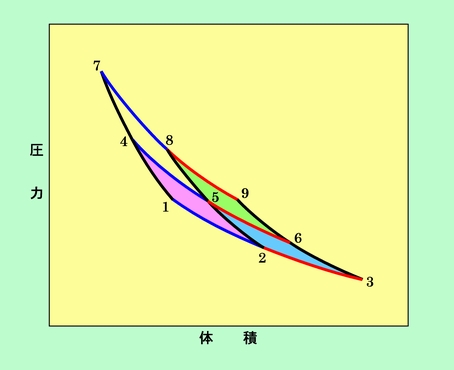
図9 カルノーサイクルを組み合わせればどこへでも行ける
ここでは、赤、青、黄、緑で表した四つのカルノーサイクルが組み合わされています。そしてサイクル上の点ならばどこへでも(どんな圧力と体積の組み合わせでも)、可逆過程で自由に移動することができ、その経路も何通りも選べます。例えば、左下の点1から右上の点9に移動することを考えましょう。経路としては、1→4→7→8→9もありますし、1→4→5→8→9もあります。その他に1→2→5→8→9とか、1→2→3→6→9とか、最短ルートだけでも6通りあります。また、1→2→3→6→5→4→7→8→9のように、行ったり来たりしながら進むこともできます。1→4→5→8→9の場合を具体的な動作で説明すると、まず断熱圧縮で温度を低温から中温まで上げ(1→4)、中温熱源から熱をもらいながら等温膨張させ(4→5)、次いで断熱圧縮して温度を高温に上げ(5→8)、最後に高温熱源から熱をもらいながら等温膨張させるのです(8→9)。これらの経路でSがどうなるかを見てみます。
前に書いたように、断熱過程ではSは変化しませんから、等温過程だけを考えればよいはずです。そして一つのカルノーサイクルでは、2ヶ所ある等温過程のSの変化量は同じ(方向は逆)なのですから、図の3本の青線のSの変化量は全て同じで、また3本の赤線のSの変化量も全て同じ、ということになります。ここまでわかった上で、もう一度それぞれの経路を見直してみましょう。すると、6種の最短経路では、青線と赤線を必ず1回ずつ右向き(熱を吸収する方向)に通っていることがわかります。また、1→2→3→6→5→4→7→8→9のような行ったり来たりのルートでも、青線も赤線も右向きに2回ずつ、左向き(熱を放出する方向)に1回ずつ通っていますので、差し引きで青、赤を1回ずつ右向きに通ったのと同じことになります。要するにどんなルートを選ぼうとも、Sの変化量は青1回分と赤1回分で、全く同じになるのです。
カルノーサイクルを組み合わせる数は、図9では4つだけでしたが、いくらでも増やすことができます。また熱源の温度差を小さくすれば、カルノーサイクルはいくらでも細かくできますので、目的とする点が(体積-圧力グラフの)どこにあろうと、必ずカルノーサイクルの組み合わせで到達することができます。つまり、どんな状態の変化でも必ずカルノーサイクルの組み合わせで再現できます。そしてその経路は無数に選べますが、どの経路を選んでもSの変化は同じなのです。このことは、Sが体積や圧力と同じ状態量の仲間であることを示しています。状態量ではない熱量を絶対温度で割ることで、状態量になってしまったのです。このSが「エントロピー」と呼ばれる量です。
実は、これとよく似たことは「仕事」にも言えます。「仕事」も「熱」と同様に状態量ではない、ということは先に説明しました。しかし気体の膨張や圧縮の仕事に関しては、「仕事」を「圧力」で割ることで、状態量である「体積」の変化量に変換できるのです。こうして見ると、エントロピーという量は、おなじみの体積や圧力、温度と同格のものであると言えそうです。実際、これまでに使ってきた気体の状態を表す「状態図」では、横軸は「体積」で縦軸は「圧力」でしたが、これを「エントロピー」と「温度」にすることもできます。ちなみに、カルノーサイクルをエントロピーと温度で表すと、図10のようになります。なんと、完璧な長方形です。等温過程では温度は一定で、熱が出入りするのでエントロピーだけが増減します。一方、断熱過程では、熱の出入りがないのでエントロピーは一定で、温度だけが増減しますから、こうなるのは当然ですね。エントロピーを使うと、こんなにキレイな形に整理されてしまうのです。考え方はちょっとわかりづらいエントロピーですが、いかに重要な量であるかがわかると思います。(なお、状態量には他にもいろいろありますが、状態量どうしの間には関係付けがされていますから、気体だけを考えている場合には、その内の2つが決まれば、後は自動的に決まってしまいます)
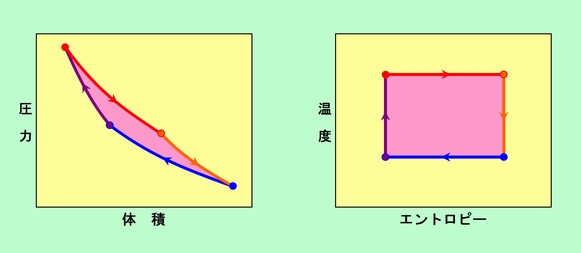
図10 カルノーサイクルを別の状態量で表す
エントロピーはこのようにして熱力学第二法則から出て来ましたが、別の視点からもエントロピーが捻り出されています。それは数学的なアプローチなのでここでは詳しくは触れませんが、要は、状態量ではない熱に何らかの係数(関数)を掛け合わせると、状態量としての性質を持った量を数学的に得ることができる、ということです。このような関数はいくらでも作れるのですが、熱力学第二法則から出て来る結果と比較すると、その関数が絶対温度の逆数であると考えるのが最も理にかなっているのです。そして熱に絶対温度の逆数を掛ける、つまり熱を絶対温度で割った値が、熱力学第二法則から出て来たエントロピーそのものであることは言うまでもありません。
エントロピーは必ず増える?
エントロピーがどういうものなのか、まだピンと来ないかもしれません。体積や圧力などと比べて、直感的にイメージしにくい量であることは確かです。その一方で、「自然に起こる変化ではエントロピーが必ず増加する」ということを聞いたことがあると思います。部屋が散らかった時に「エントロピーが大きくなった」などと言うこともあるぐらいですから・・・・。しかし、本当にエントロピーは必ず増加するものなのでしょうか? エントロピーのイメージを作る助けにするためにも、これまで出て来たいくつかの例で、エントロピーの増減を確認してみましょう。
まず、図3の3つの例を見てみます。画面上で長い距離をスクロールするのはたいへんでしょうから、ここにもう一度図3を表示しておきます。

図3(再び)
図3(a)では、注射器内の空気は湯から熱をもらって膨張しています。この時、温度が一定なので内部エネルギーは変化しませんから、もらった熱は全て仕事に変わっています。この熱(=仕事)を温度で割った分だけ、エントロピーは増加することになります。特に問題はありませんね。それでは、これを逆向きに動かしたらどうなるでしょうか。今度は温度一定で圧縮されるのですから、外からされた仕事に相当する熱が発生します。この熱は注射器から湯に放出されることになりますから、注射器内の空気のエントロピーは減少します。このように、変化の仕方によっては、エントロピーは増えることもあれば減ることもあるわけで、決して「常に増加する」という類のものではないのです。
次に図3(b)は少々ややこしいので後回しにして、先に図3(c)について考えます。今度も膨張中に熱を吸収しますから、ここでエントロピーが増加します。ところが不可逆過程(圧力差がある状態での膨張)であるために、熱量を温度で割ってもエントロピーを求めることはできません(熱量を温度で割るとエントロピーが求まる、というのは可逆過程に限った話です)。ならばお手上げかというと、そんなことはありません。エントロピーが状態量であることを思い出してください。途中の過程に関係なく、最初と最後の状態が決まっていれば、エントロピーの値は決まるはずです。ということは、図3(c)のエントロピー増加量は、改めて計算するまでもなく、図3(a)と全く同じはずなのです。このように、計算が難しい、あるいは不可逆過程のために計算ができない、という場合でも、可逆過程に置き換えてエントロピーを求めれば、それぞれの状態に対応するエントロピーはちゃんと求めることができるのです。
それではここでちょっと視点を変えて、外側の湯も含めた全体でエントロピーを見てみましょう。まず図3(a)ですが、湯の立場から見れば、注射器に熱を奪われた分、エントロピーは減少します。その量は、注射器の方で増えたエントロピーとピッタリ一致しますから、全体では差し引きゼロ。つまりエントロピーの増減はありません。実はこれは可逆過程全般に言えることで、熱のやり取りをする要素を全部含んだ全体で見れば、エントロピーは変化しないのです。
次に図3(c)について見てみましょう。先ほど書いたように、注射器側でのエントロピーの増加量は図3(a)と全く同じでした。それでは湯の方のエントロピーの減少量も同じかというと、実はそうではありません。前にも書いたように、図3(c)はピストンを押す圧力が弱く、その分、外に対する仕事が少ないですから、湯から吸収する熱量も少なくなっています。と言うことは、温度が同じで移動した熱量が少ないのですから、湯の方のエントロピーの減少量は、図3(a)よりも小さいことになります。注射器側のエントロピーの増加量が同じなのに、湯の側のエントロピーの減少量は少ない・・・つまり図3(c)の全体のエントロピー変化はゼロではなく、増加していることになるのです。どうやら不可逆過程を含む場合には、全体のエントロピーは増加するようです。
それでは図3(b)はどうでしょうか。前半の膨張過程は熱の出入りのない可逆膨張ですから、エントロピーの変化はありません。エントロピーの増加は、最後に注射器を温めて元の温度に戻すところで起こります。温度が変化しているので簡単には計算できませんが、最初と最後の状態が図3(a)と同じなのですから、注射器側のエントロピーの増加量も図3(a)と同じ、ということで問題ないでしょう。一方、湯の方に目を移してみましょう。湯が注射器内の空気に与えた熱量は、空気が膨張する時にした仕事と同じはずですから、図3(a)よりは少ないはずです。それではエントロピーはどうか、ということですが、これは温め方によって結果が変わります。
最も簡単な温め方は、最終目標の温度(つまり図3(a)と同じ温度)の湯に浸す方法でしょう。この場合は内外で温度差がありますので、不可逆な加熱になります。温度は図3(a)と同じで、湯から出て行く熱量は少ないのですから、エントロピーの減少も少ないはずです。つまり、注射器側で増えたエントロピーよりも湯側で減ったエントロピーの方が少ないわけで、全体のエントロピーは増加することになります。これに対して、温めを可逆的にやったらどうでしょうか。この場合は、少しずつ温度の違う湯をたくさん用意して、温度の低い方から順番に浸して徐々に注射器を温めて行くことになります。この時、湯から出て行ったトータルの熱量はさっきと同じで図3(a)よりも少ないのですが、温度も図3(a)よりも常に低いことになります。ということは、熱量を温度で割ったエントロピー変化は、初めから高温の湯に浸して不可逆に加熱した時よりも大きいことになります。結果的に、注射器側で増えたエントロピーと湯側で減ったエントロピーがつり合って、全体のエントロピーは変化しない、ということになるわけです。
もう一つ、図8の場合についても見てみましょう。今度は熱機関の内部で何が起こっているかはわかりませんが、熱機関はサイクルを一回りすると元の状態に戻るのですから、エントロピーも一週回って元に戻っているはずです。つまり熱機関そのもののエントロピー変化はゼロですから、熱源の熱の出入りだけを考えればいいのです。

図8(再び)
まず、左端の図の機関Aを可逆機関であるとしましょう。高温熱源からもらう熱は多く(太い赤矢印)、低温熱源に捨てる熱は少ない(細い赤矢印)ですが、温度も同じ割合で違いますので、熱量を温度で割ったエントロピー変化は同じです(これは可逆機関の基本的な性質でしたね)。つまり、高温熱源で減ったエントロピーと低温熱源で増えたエントロピーは同じですから、全体のエントロピー変化はゼロ、ということになります。次に機関Bですが、これは捨てる熱が多く取り出せる仕事が少ない、いわゆる効率の悪い熱機関です。ということは、機関Bは不可逆機関であるはずです(可逆機関は常に最大効率ですから)。高温熱源からもらった熱量は機関Aと同じですが、低温熱源に捨てる熱量は機関Aよりも多いので、高温熱源で減ったエントロピーよりも低温熱源で増えたエントロピーの方が多いことがわかります。つまり不可逆機関では、サイクルを一回りした時の全体のエントロピーは増えてしまうのです。
ついでに、図8の中央の図や右端の図についても考えてみましょう。中央の図では可逆機関Aを逆運転しています。熱源の側から熱の出入りを見てみると、高温熱源では差し引きゼロですが、低温熱源では入りの方が多いですから、熱源全体で見れば入超で、全体のエントロピーは増えています。全工程の中に機関Bという不可逆機関が入っているために、エントロピーが増えてしまったのです(両方ともが可逆機関なら熱の出入りは同じですから、エントロピー変化は起こりません)。逆に右端の図では低温熱源が出超になっているので、全体のエントロピーは減っています。しかし機関Bは可逆機関ではないのですから、これを逆運転することは実際にはできません。つまり、このようなエントロピーを減少させる組み合わせは、現実には作れないのです。もちろん外から何らかの操作を加えれば、エントロピーを減少させることは可能です。しかしその場合には、「外」という新たな要素が加わりましたから、その「外」も含めなければ全体を見たことにはなりません。そして、その「外」のエントロピーは、「内」のエントロピーが減った以上に増加しているはずです。要するに、それ以外に「外」のない閉じた状態を考えれば、全部が可逆過程ならばエントロピー変化はゼロになりますし、そうでない場合(不可逆過程を含む場合)は、エントロピーは必ず増加するのです。これが「エントロピーは増加する」という言葉の本当の意味です。
【補足】 統計力学では分子の位置や運動などのミクロな状態を基にして、そこから圧力や体積などのマクロな状態を考えて行きますから、エントロピーの捉え方も熱力学とは全く違っています。このことにも、ちょっとだけ触れておきましょう。
例えば、2個のサイコロを同時に振って、その時に出た目の合計はいくらになるかを考えます。最も小さい数は2(両方1)で、最も大きい数は12(両方6)ですね。これらは一通りの組み合わせしかありません。しかし、合計が5の場合は、2個のサイコロを区別した場合、(1,4), (2,3), (3,2), (4,1)の4通りが考えられますし、最も組み合わせが多い7の場合には、全部で6通りあります。当然、組み合わせの多い方が出る確率は高くなります。自然現象も同じで、組み合わせが多い状態の方が出現しやすい、と考えます。気体が、ある体積と圧力の状態(マクロな状態=サイコロの目の合計に対応)にある時、この状態を実現するための分子の位置や運動の状態(ミクロな状態=個々のサイコロの目の組み合わせに対応)は一通りとは限りません。実際に、無数の組み合わせが可能です。また別の体積と圧力の状態に対しては、また別の多数のミクロな状態が対応しています。一つのマクロな状態が、多数のミクロな状態を従えているのです。そして配下にいるミクロな状態の数が多いほど、そのマクロな状態が現れやすくなる(現れる確率が上がる)ということです。このミクロな状態の数を表す指標として、エントロピーが定義されるのです。
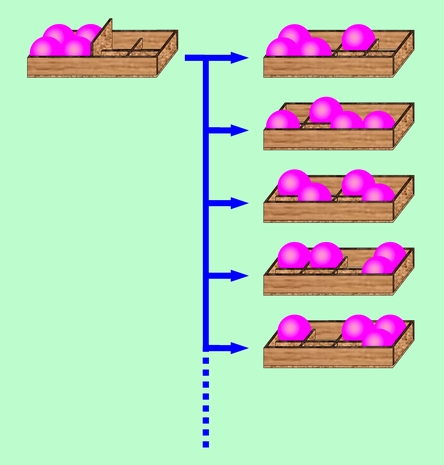
こんな例を考えましょう。真ん中で仕切られた2つの部屋があり、それぞれの部屋には4つの小部屋があります。小部屋の仕切りは、ボールの移動を妨げるほど高くはないとします。初め、左の部屋にだけ、各小部屋に1個ずつ、計4個のボールが入っていたとしましょう。ここで真ん中の仕切りを取り払って全体を揺すると、ボールは適当に散らばりますね。その時のボールの配置の仕方が何通りあるかを計算してみると、下のようになります(ボールは区別できないとします)。
| 左の部屋のボール数 |
右の部屋のボール数 |
配置の数 |
| 4 |
0 |
1 |
| 3 |
1 |
16 |
| 2 |
2 |
36 |
| 1 |
3 |
16 |
| 0 |
4 |
1 |
| 計 |
70 |
左右均等になる場合が最も数が多いことがわかりますね。つまりこの状態がエントロピー最大で、最も現れやすい、ということです。
小部屋とボールの数をもっと増やして10や100にすると、配置の数の分布はもっと極端になります。それを示したのが下の図です。
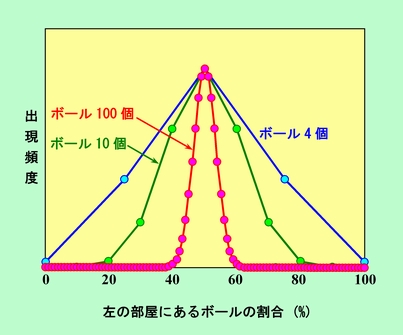
補足図
ボールの数が100個で既にこれだけ中央が突出するのですから、実際の気体分子の数ともなれば、ほとんど左右均等の状態しか現れないことは容易に想像できるでしょう。どこかに分子が多く集まって圧力が高くなる、といった極端な状況はほとんど起こり得ないのです。
この例に限らず、秩序立った状態よりも乱雑に散らばった状態の方が、その状態に対応するミクロな状態の数は多くなります(制限が少ないですから)。その意味で、エントロピーは無秩序さの程度、乱雑さの程度を表す、という言い方もできるのです。
統計力学ではさらに、エントロピーを一定量増やすのに熱がどれくらい必要か、ということで温度を定義します。たくさん熱を与えなければエントロピーが増えない状態を温度が高い状態、少しの熱でエントロピーが大きく増える状態を温度が低い状態とするのです。イメージとしては、温度が高い状態では分子が激しく動き回っていて既に相当に「乱雑・無秩序」な状態にあるため、少々の熱をもらったぐらいでは「乱雑さ」はたいして増加しない、といったところでしょう。
熱力学では、可逆機関についてあれこれ考えている中から温度というものを定義し、そこからエントロピーをいう考え方を引き出しました。一方、統計力学では、先にエントロピーを理論的に定めて、そこから温度を定義しています。熱力学ではものすごく概念的でわかりにくかったエントロピーが、統計力学では非常に明確に定められているわけで、その意味では統計力学の方が理解しやすいかもしれません。
エンタルピーを忘れている?
熱力学を勉強したことがある人なら、何か大きな忘れ物をしているような気がするかもしれません。そう・・・・教科書ではたいてい初めの方で出て来る「エンタルピー」が、まだ出て来ていないのです。この「エンタルピー」・・・・、名前がよく似ているので「エントロピー」とセットになる量であるかのようによく勘違いされますが、実際にはほとんど関係ありません。エントロピーはこれまでに長々と説明して来たように、熱力学の基本法則にかかわる非常に重要な量です。これに対してエンタルピーは、実はたいして大きな意味がある量ではないのです(こんなことを言うと叱られそうですが、個人的には、知らなくても大きな問題はないように思えます)。
具体的にはエンタルピーは、内部エネルギーに体積と圧力の積を加えたものです。こういう量を定義しておくと、比熱などを考える時に式の形が非常に簡単になりますし、エンタルピーを一定に保つような変化もありますので、いろいろと便利な点はあります。また、化学反応などで熱が発生した時に、その熱が温度を上げるだけでなく、気体の体積の増加に使われる場合が多いですから、「反応熱」と言うよりも「反応エンタルピー」と言った方が誤解が少なくなる、ということもあるでしょう。しかしながら、例えば反応熱の話にしても、熱が内部エネルギーと膨張の仕事に分配されることをちゃんと理解していれば誤解することはないわけで、エンタルピーを考えないと現象が全く説明できなくなる、というほどのものではありません。というわけで、エンタルピーに関しては、本稿ではこれ以上は触れないことにします。
最後に現実的な話をちょっと・・・
熱力学、特にエントロピーの話は、正直言ってなかなかわかり難いものです。ちょっとキツネにつままれたような、現実離れした感じがしているかもしれません。そこで最後に、現実的な話を少し・・・・。
蒸気機関
元々熱力学という分野は、産業革命時に盛んに使われるようになった蒸気機関に関わりながら発達して来たものですから、これを外すわけには行きません。蒸気機関のタイプはいろいろありますが、模式的に描くと、図11のような感じでしょう。典型的な状態図のパターンも併せて示しておきました。
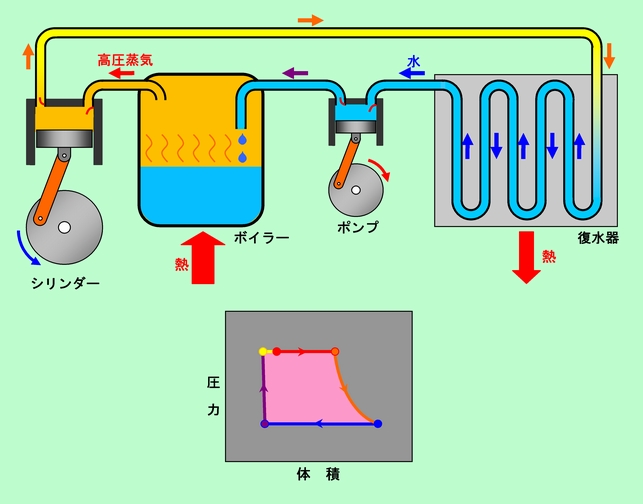
図11 蒸気機関
まずボイラーで湯を沸かし、沸点まで温度が上がった状態からスタートします。状態図で言えば、赤丸の状態です。ここからさらに加熱を続けると、水(湯)はどんどん蒸発し、高圧の蒸気が作られます。液体が蒸発している間は温度は変わりませんが、蒸発熱をどんどん吸収しますからエントロピーは増加し、体積も大きくなります(状態図の赤線)。厳密に言えば、赤線上を動くのではなく、赤丸の状態の液体と、橙丸の状態の蒸気が共存していて、液体の量が減少、蒸気の量が増加している状態です。この高圧蒸気をシリンダーに送り込み、蒸気の圧力でピストンを動かして動力を取り出します。ここでは断熱膨張に近い状態になっており、エントロピーは一定ですが体積は増加、圧力は減少、温度も減少します(状態図の橙線)。ピストンから排出された蒸気は復水器と呼ばれる冷却装置を通して水に戻します。この時も、蒸気と水が共存している限りは温度、圧力は一定で、エントロピーと体積が大きく減少します(状態図の青線)。凝縮した水は、循環ポンプで水圧をボイラーの圧力まで高めた上で(状態図の紫線)、ボイラー内に戻されます。ボイラーに戻った水は再び沸騰する温度まで加熱されて(ちょっと短いですが、状態図の黄線)、元の赤丸の状態に復帰することになるのです。
実際の蒸気機関では、ピストンの両側に交互に蒸気を送り込んで、「押し」「引き」の両方で力を出すようになっていたり、ピストンから排出された蒸気(まだ圧力がそこそこ高い)を使って2段目、3段目のピストンを動かしたりと、いろいろな工夫がされています。
他の熱機関も、基本的には図11の蒸気機関とそんなに大きく違っているわけではありません。蒸気をシリンダーに送るのではなく、タービンを回すようにすれば、火力発電などで使われる蒸気タービンになります。また、ボイラーを使って高圧ガスを作るのではなく、シリンダーの内部で燃焼させて圧力を発生させると、ガソリンエンジンなどの内燃機関になります(この場合は媒体を循環させるのではなく、使い終わったら外に捨てて、新しく燃料と空気を送り込むことになりますが)。
エアコン
エアコンや冷蔵庫などの原理は、基本的には図7のカルノーサイクルの逆運転ですが、現実の機械の仕組みは、ピストンを引いて体積を増加させる方式とは少し違います。実際にピストンのようなものを動かして体積を増加させようとすると、相当大きなサイズが必要になりますし、機構的にも大掛かりになるからです。そこでエアコンなどでは、図12のような方式が主に使われています。中で膨張したり収縮したりするガス(冷媒)には、昔はフロンが使われていましたが、上空のオゾン層を破壊するということで、現在では塩素を含まない別の物質にほとんど置き換わっています。
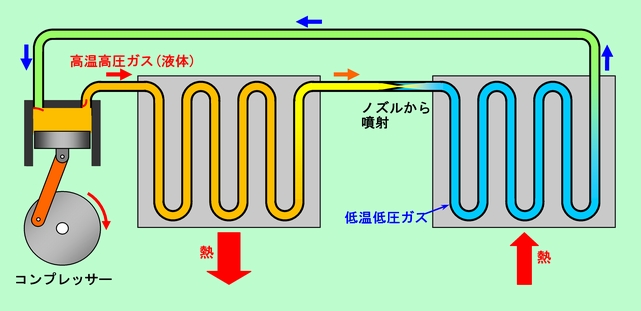
図12 エアコンの原理
まず左端のコンプレッサーで、冷媒のガスを圧縮します。普通のエアコンでは、圧力は20気圧程度です。断熱圧縮に近い状況ではありますが、現実的な速度で圧縮されますから、もちろん可逆ではありません。ここで圧縮の仕事が熱に変わり、高温高圧の状態が作られます。さらに、冷媒には沸点が室温付近の物質が使われているので(冷媒の種類によってかなり幅はありますが)、一部液化も起こります。液化が起こると凝縮熱が放出されますから、それも加わって温度はいっそう高くなるのです。この高温ガス(+液体)がぐにゃぐにゃ曲がった管の中を通過する間に、外に熱を放出します。夏場の冷房の場合であれば、この部分は室外機に当たり、管内のガスは外気温よりも高くなっているので、熱を戸外に放出することになるのです(実際のエアコンでは、表面積の大きいフィンを管に取り付け、そこにファンで風を送って、放熱の効率を上げています)。
熱を放出したガスは少し温度が下りますが、まだまだかなり熱い状態です。次の段階では、(冷房の場合は)このガスを室内機に運び、ノズルから噴射して一気に膨張させます。これまで考えて来た熱機関とは、この部分が大きく違っています。これまでの熱機関では、ガスに(ピストンを押すなどの)仕事をさせて温度を下げていました。しかしここでの膨張は、体積が固定されている容器内への膨張ですから、外に対しては仕事をしていません(噴射されたガスの塊の立場から見れば、高圧側では押し出されて仕事をされ、低圧側では周りを押しのけて仕事をしていますから、差し引きゼロです)。ですから本来ならば温度は下らないはずです。ところが、それは分子の大きさも、分子間の引力も働かない理想的な(頭の中で考えた)気体の話であって、実際の気体では、このタイプの膨張でも温度は変化するのです。温度が上がるか下がるかは気体の種類と温度によって変わりますが、室温付近では(水素などの一部のガスを除いて)ほとんどのガスで、このタイプの膨張によって温度は下がります。さらに液化していたものが一気に気化しますので、蒸発熱が奪われて、温度はさらに低下することになります。この冷えたガスが周囲の空気から熱を奪い、部屋の中を冷やすのです。そして再びコンプレッサーに入り、圧縮されて高温高圧状態に戻ることになります。
フェーン現象
日本では、南風が吹いて暖かい空気を運んで来ると、気温がグングン上がります。最近では気温の最高記録も次々に更新されていますね。その最高温度を記録している地域は、と言うと、南風が直接当たる太平洋側ではなく、一山二山越えた盆地や日本海側であることがわかります。これが「フェーン現象」による、ということは、天気予報などでもよく言われていますからご存知でしょう。そしてそのフェーン現象には、気体の膨張・圧縮による温度変化が関わっています。
南から湿った暖かい空気がやって来て山にぶつかり、山肌に沿って斜面を駆け上がります。この時、上空に行くほど気圧が低いので、空気の塊は膨張し(ほとんど断熱膨張に近い状態です)、温度は急激に下がります。このまま山を越えて反対側に降りてしまえば、再び圧縮されて元の温度に戻るだけですが、実際にはそうは行きません。上空で温度が下がった時に、空気に含まれていた水蒸気が凝縮して雲を作り、雨を降らせます。ここで多量の凝縮熱が放出されますから、空気の温度は断熱膨張で予想されるほどは下がらないのです。その結果、乾いた空気が山を下って圧縮された時には、元の温度よりも高くなってしまうのです(水を蒸発させて蒸発熱を奪おうにも、水は山の手前で雨になって失われていますから、もうどうしようもありません)。
雑科学ホーム
hr-inoueホーム
















