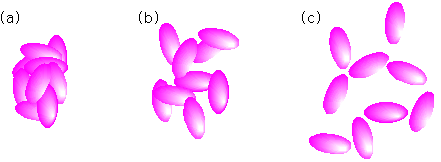雑科学ホーム
hr-inoueホーム
● 微粒子分散系の話 ●
活躍する分散系
「微粒子分散系」などと言うと、何やら難しいもののように聞こえますが、要するに、固体や液体の小さな粒子が液体(気体や固体の場合もなくはないですが)の中に混ざっているもののことです。こういう目で周囲を見ると、いたるところに分散系があることに気付きます。冷蔵庫を開けると、(たぶん)牛乳が入っていますね。これは脂肪の粒子が水に分散したものです。マヨネーズもあるでしょう。これも油の粒子が酢や水が混ざった液の中に分散したものです。バターやマーガリンは逆に、水系の粒が油に分散しています。ドレッシングの類も、水系の部分と油系の部分が互いに分散しています(分散が悪くて、放っておくと分離するものも多いですが)。化粧品や塗り薬でクリーム状のものは、大抵、油系の粒が水に分散したものです。自転車のベアリングの潤滑などに使われるグリースでは、油の中に粘度を高める薬剤や水が分散しています。これらの例は液体中に液体粒子が分散したもので、エマルション(乳濁液)などと呼ばれます。
固体の粒が液体に分散した系もたくさんあります。ペンキや絵の具などでは、顔料と呼ばれる色素の粒が水や油に分散しています。これらを含めて、塗料と呼ばれるものの多くは分散系と言ってよいでしょう。墨汁なども、ススが水に分散した分散系ですね。傘やレインコートなどにかけて水をはじくようにする撥水剤の中には、テフロンの微粒子を溶剤に分散させたものがあります。ちょっと変わったところでは、磁性を持った微粒子を油に分散させた磁性流体などもあります。液体でありながら、磁力をかけることで流れを止めて一箇所に留めることができるので、真空装置の回転軸シールや、宇宙服のヘルメットの回転部分などに使われています。磁性流体とは少し違いますが、ビデオテープの記録層なども、磁性を持った粒子を分散させた塗料を塗って作ります。かつてはハードディスクも同じで、私の
学位論文のテーマでもありました。
本稿では、後の方の、固体が液体に分散した系について主に見て行きます。
なぜ分散が可能なのか
液体どうしならともかく、重い固体がどのようにして液体中で安定に分散するのでしょうか。これには2つの要素がかかわっています。
一つは、粒子が十分に小さい、ということです。どのくらい小さければよいかというと、大体0.1μm(100nm)以下、ということになります。これよりも小さいと、自分の重さで沈む速度と、周りの液体分子の衝突によって揺り動かされる(いわゆるブラウン運動です)速度とがほぼ同じになって、すなおに沈めなくなるのです。もちろん固体粒子と液体の比重差や粘度などによって違いは出てきますが、およその目安にはなるでしょう。詳しい理論や計算方法は界面化学などの教科書に載っていますから、ここでは省略します。
もう一つの要素は、粒子どうしがくっ付かない、ということです。いくら小さな粒子を準備しても、それが互いにくっ付いて大きくなってしまっては元も子もありません。安定な分散系ができるかどうかは、この粒子どうしのくっ付き(凝集)をいかに防止するかにかかっているのです。
粒子の凝集を防ぐポイントの一つは、「粒子どうしの相性よりも、粒子と液体(溶媒)との相性をよくする」、ということです。これは液体どうしに話を置き換えてみればわかりやすいでしょう。例えば水と油。激しく攪拌して水の中に油を細かく散らしても、油は水との相性がよくありませんから、油どうしでくっ付いて、すぐに2つの層に分離してしまいます。これと同じことが固体の分散系でも起こります。どちらかと言うと水になじみやすい金属酸化物の粒子を有機溶媒に入れると簡単に凝集してしまいますし、逆に有機溶媒となじみやすい有機顔料などでは、水に入れると塊になってプカッと浮いてしまいます。これに対して、固体となじみのよい溶媒を選んでやると、粒子の周りを溶媒分子が取り囲んで安定になりますから、凝集しにくくなるのです。それでも、どうしても相性の悪い溶媒を使わなければならないケースがままあります。そんな時は粒子表面にちょっとした細工をしなければなりません。その最も簡単な方法は、粒子との相性が良い部分と溶媒との相性が良い部分を併せ持つ物質を加えることです。いわゆる
界面活性剤ですね。これによって粒子表面と溶媒とを仲良くさせるのです(図1)。
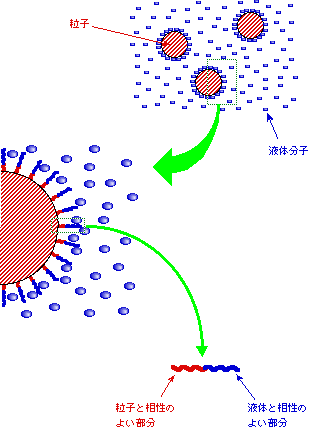
図1 粒子表面と液体とを仲良くさせる
これは誰でも知っている当たり前の方法ですね。ところが、水と油を界面活性剤で混ぜ合わせるぐらいならばすぐにできますが、固体粒子の分散となると、なかなか適当な活性剤が見つからないのです。もちろん、この手の粒子にはこの活性剤、という指針はありますが、それでも最適な組み合わせを見つけ出すのは容易ではなく、結局はジュウタン爆撃、ということがよくあるのです。
このように粒子と溶媒の相性をよくしてやればそれで良いかと言うと、必ずしもそうではありません。物と物との間には「分子間力」と呼ばれる引力があり、粒子間にもこの力が必ずはたらきます。分子間力と言うと微小な力の代名詞みたいなところがありますが、相手が小さな粒子となると、この力はけっこう効きます。特に距離が近くなると急激に強くなる性質があり、溶媒のバリアーなど簡単に突破して凝集を起こしてしまうのです。このような分子間力による凝集を防ぐ方法として、粒子どうしを不仲にする、ということが行なわれます。その方法には、大きく分けて2種類あります。
電荷の反発を利用した分散
まずは、電気的な力を利用する方法です。粒子表面に元々ある官能基を解離させたり、電荷を持った物質を粒子表面にくっ付けたりすることで、粒子表面にプラスかマイナスの電荷を持たせるのです(図2)。
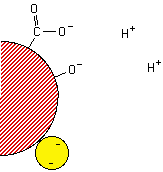
図2 粒子表面に電荷を持ち込む
静電場の話でも少し触れましたが、このようにして電荷を持った粒子は、互いに反発して凝集しなくなるのです。ただし分散系の場合には粒子の周りに溶媒がありますから、真空中や空気中での電荷の反発とは少し状況が違っています。その様子を図3に示しました。ここでは、粒子の表面にプラスの電荷がある場合を例に取っています。
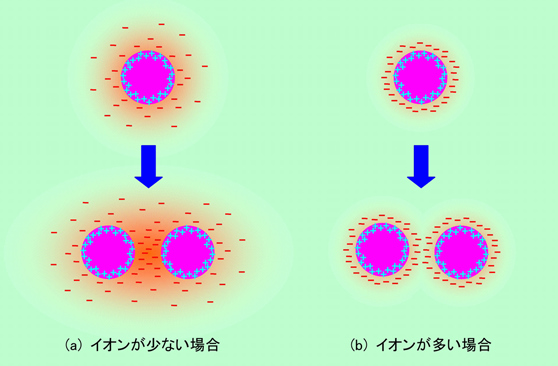
図3 粒子の周りの電荷の様子(粒子の電荷がプラスの場合)
静電場の話で出て来たようなフリーの電荷の場合と違って、粒子の電荷の周りには溶媒中のマイナス電荷が集まって来ます。マイナス電荷の一部は粒子のすぐそばにありますが、一部は液の中に広がっていて、全体として電荷が中和された状態になっています。これがいわゆる電気二重層で、電荷を蓄えるコンデンサーみたいなものですね。電気二重層の外側から見れば、粒子表面のプラス電荷は、周りのマイナス電荷で相殺されて、全く見えなくなっています。さて、このような電気二重層の衣をまとった2個の粒子が接近して来たとしましょう。すると図3下のように、マイナス電荷の群れが重なって来ます。つまり、互いの電気二重層が重なり合って、お互いの中に侵入するのです。この電荷の重なりによって反発力が働いて、粒子は離れて行くことになります。
液の中にたくさんのイオンが溶け込んでいると、図3(b)のように、多くのマイナスイオンが粒子のすぐ近くに寄って来ます。つまり電気二重層が薄くなるわけで、このような場合は、粒子がかなり接近しないと電荷の重なりは発生しません。そのため、電荷の反発が始まるころには引力の方がどうしようもないくらいに大きくなっている、ということも起こり得ます。こうなるともうダメで、粒子はすぐに凝集してしまうことになります。
このあたりのことをエネルギーの大きさで表したのが図4です(球形粒子の場合の計算結果です)。横軸は、ある粒子の表面と隣の粒子の表面との間の距離で、左端が粒子が接触した状態になります。縦軸はエネルギーで、粒子が遥か彼方に離れている時のエネルギーをゼロとし、不安定な方向をプラス、安定な方向をマイナスに取って表示しています。分散系は当然、できるだけ安定になろうとしますから、図では下方、つまりマイナスの方向へ行こうとします。エネルギーは山の高さのようなものですから、ちょうど山の斜面に置かれたボールが低い方へ転がり落ちるようなものですね。
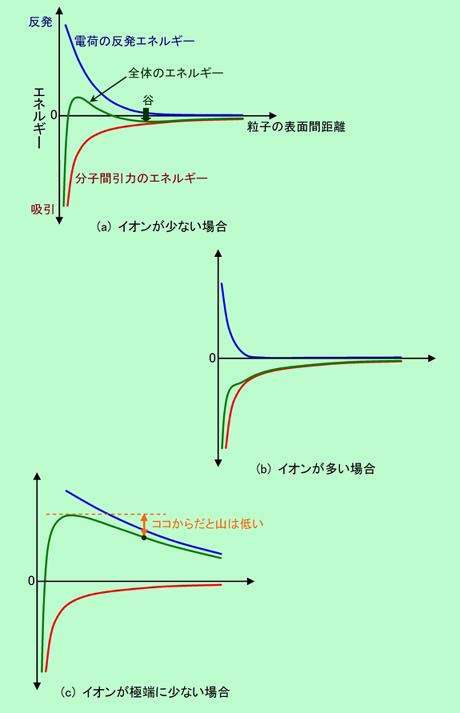
図4 粒子間の距離が変わるとエネルギーは変化する
図3と同じように、図4(a)は液中のイオンが少ない場合です。図の中の青線が電荷による反発のエネルギー、赤線が分子間力による引力エネルギー、そして緑線がその両方を足し合わせた全体のエネルギーを表しています。引力のエネルギーも反発力のエネルギーも、粒子間の距離が狭くなると急激に大きくなりますが、その大きくなるなり方はちょっと違っています。まず、ずっと遠いところでは引力が優勢です。これは図3のマイナスイオンの重なりがまだほとんど効いていないためで、全体のエネルギーも引力の方に引きずられています。ところが粒子が接近してくると、反発力の方が先に立ち上がりますので、全体のエネルギーは反発側に振れます。そしてさらに接近すると、引力の急激な増加が効いて、全体も引力側に落ち込むことになります。これを粒子の動きで見てみましょう。初め遠くに離れていた2個の粒子が、緩やかなエネルギーの斜面に沿って徐々に近づき、谷の部分(緑の矢印)で止まります。ここから先にはちょっとした小山があるので、これ以上は接近できませんが、何かのはずみでこの小山を越えてしまうと、あとは奈落の底に一直線。2個の粒子はガッチリとくっ付いてしまいます。このことからわかるように、重要なのは小山の高さです。粒子は熱エネルギーによって振動していますが、少しぐらい激しく振動しても簡単には越えられないぐらいに小山が高ければ、粒子は凝集しないのです。谷に止まっている状態も凝集と言えば凝集なのですが、遠く離れた時とのエネルギー差はわずかですから、ちょっとかき回してやれば、簡単に引き離すことができるのです。また条件によっては、ずっと遠くから反発力が効いて、谷を経ずに小山につながる場合もあります。この場合はもっと分散性がよい、ということになります。
小山の高さには、粒子の大きさや溶媒の誘電率などのいろいろな要素が影響します。液中のイオンの量も大きな要素の一つで、イオンがたくさんある場合には、図4(b)のようにエネルギーの状態はガラッと変わります。粒子がかなり接近するまで電荷による反発が効かないために、図4(a)のような小山ができず、一気にズドーンと落ち込んでしまうのです。微粒子が分散した液に塩などを加えて凝集を起こし沈殿させる「凝析」という方法がありますが、これはまさに、図4(a)の状態から図4(b)の状態に変化させているのです。
逆に液中のイオンが極端に少ないと、エネルギーは図4(c)のようになります。水ではない有機溶媒の場合に、このような形になることがあります。今度は遥か彼方から反発力が働くので、粒子は全く凝集しない・・・・・かと思いきや、必ずしもそうではありません。確かに、エネルギーがゼロに近くなるぐらいに粒子が遠くに離れていれば、それなりの分散効果は期待できるでしょう。ところが粒子の数が多くなると、初めから粒子どうしの距離が近くなりますから、スタート地点が既に小山の中腹、ということもあり得ます。例えば、粒子の体積が液全体の10%ぐらいになると、粒子表面間の距離は、粒子の直径よりも小さくなります。図4で言えば、粒子が均一に分散した状態で既に横軸の真ん中あたりまで接近している、ということも、そう珍しいことではないのです。こうなると実質的な小山の高さはそれほどでもないですから、粒子は案外簡単に小山を越えて凝集してしまうこともあります。高い山を麓から登るのは大変ですが、8合目からならば大したことはない、ということです。また有機溶媒の場合は、そもそもイオンへの解離が起こらず、電荷がほとんど発生しない場合もあります。こうなると、電荷による反発はあてにできませんから、何か別の方法で分散させなければなりません。
ところで、どんな条件が揃ったら適当な高さの小山ができて安定に分散するのでしょうか。これは非常に難しい問題で、関連する要素が多すぎて、一言ではとても言えないというのが実情です。それでも思いっ切り乱暴に言ってしまえば、0.1μmぐらいの粒子の場合、特に意識的に物を溶かしていない水中で、数十〜100mV程度のそこそこの電荷を持たせてやれば安定に分散する、ということになります。これよりも粒子が小さくなったり、水中に溶けているものが増えたりすれば、小山は低くなって、凝集が進むのです。
粒子表面の帯電 --- 電荷ゼロ点と等電点
粒子表面に電荷を持たせる話が出て来たので、ここで粒子表面の帯電について少し触れておきましょう。
固体粒子の表面には、解離性の基がある場合が多々あります。金属や酸化物の粒子では、その表面はほとんど水酸基で覆われていますし、カルボキシル基やスルフォン基などを導入することもできます。例として水酸基を取り上げてみましょう。

図5 表面水酸基の解離
水酸基を持つ粒子を水に入れた場合、その水が酸性ならば、水中に多量にある水素イオンが水酸基にくっ付いて、粒子表面はプラスに帯電します。逆に水が塩基性ならば、水中には多量の水酸化物イオンがありますから、これが水酸基の水素を剥ぎ取って、粒子表面はマイナスに帯電します。そして、その中間には、粒子表面がプラスにもマイナスにも帯電しないところがあるはずです。これが電荷ゼロ点(point of zero charge = pzc、または、zero charge point = zcp)で、普通は対応する水素イオン指数(pH)で表します。この値は物質によっていろいろで、シリカでは酸性側(pH=4附近)、アルミナでは塩基性側(pH=9〜10)にあることはよく知られています。
電荷ゼロ点を求めるには、次のようにします。
まず、酸性にした水を用意します。これに、pHを計りながらアルカリを滴下して、いわゆる滴定曲線を描きます。これがブランクになります。次に、同じ酸性水に目的の粒子を投入して、同様に滴定曲線を描きます。その結果は図6のようになるはずです。(ただし、ある種の酸化物では酸性の水に溶けてしまうものもありますので、そのような場合には、アルカリ側から滴定を始めます)
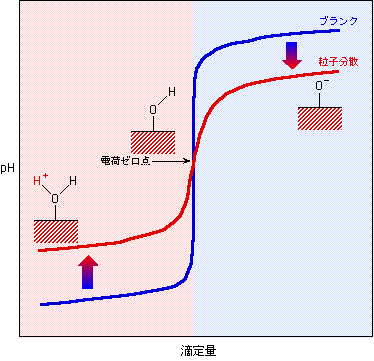
図6 電荷ゼロ点の求め方
図の左側の領域では、水中の水素イオンが水酸基に捕まって減少しますから、液のpHはブランクよりも高く(中性よりに)なります。一方右側の領域では、逆に水酸基から水素イオンが供給されますから、液のpHはブランクよりも低く(やはり中性よりに)なります。そして、2つの滴定曲線が交わったところでは、粒子の有無に関わらず状態が同じなのですから、粒子表面は何の働きもしていない、言い換えれば電荷を帯びていないことになります。これが電荷ゼロ点です。
ところで、電荷ゼロ点とまぎらわしいものに等電点(isoelectric point = iep)があります。この両者は、全く同じ意味として扱われている場合も多いのですが、別のものとして区別する人もいます。等電点の定義は、「プラス電荷とマイナス電荷の総和が等しくなる点」、というもので、現象としては、「電場をかけた時に一方向への電気泳動を起こさない点」、ということになっています。これだけを見ると電荷ゼロ点と同じに思えますね。ところが、それは電荷に関与するのが解離するイオン、つまり水酸基の例で言えば水素イオンである場合に限られるのです。表面水酸基を持つ粒子に、何らかの原因で別のイオン(例えば塩素イオン)が吸着した場合を考えましょう。液のpHを電荷ゼロ点に調整すると、水酸基の解離、あるいは水素イオンの付着は起こりません。しかし、塩素イオンが吸着しているために粒子はマイナスに帯電していますから、電気泳動をさせると、正極側に動いてしまいます。つまりこの点は、電荷ゼロ点ではあっても等電点ではないわけで、等電点はさらに酸性側(少し水素イオンを付着させて、塩素イオンのマイナス電荷を打ち消した点)にあることになります。このように考えると、電荷ゼロ点と等電点とは別のものとして扱った方がよさそうです。
吸着した高分子の反発を利用した分散
電気的な力とは別に、粒子の表面に高分子の厚い吸着層を付けて、その立体的な反発力で凝集を防ぐ方法があり、電荷を持たせにくい有機溶媒の系でよく使われます。その高分子はもちろん、(少なくとも一部分は)溶媒との相性が良い、つまりある程度は溶媒に溶けるようなものでなくてはなりません(そうでないと高分子どうしがくっ付いて凝集してしまいますから)。このような高分子の衣を着た粒子が接近するとどうなるかを考えてみましょう。
高分子の吸着層は硬いプラスティックの殻のようなものではありません。元々溶媒に溶けやすいわけですから、吸着層にも相当な量の溶媒が取り込まれています。普通の高分子の吸着層では70%〜90%ぐらいが溶媒、逆に言えば、高分子の濃度は10%〜30%程度で、むしろちょっと濃い目の溶液、といった状態なのです。そのため粒子が接近して来て吸着層どうしが接触しても、カチンと跳ね返すのではなく、図7左のように吸着層が重なったり、図7右のようにへこんだりすると考えられています。
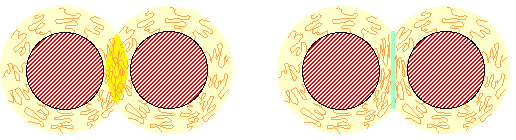
図7 高分子吸着層を持った粒子が接触すると・・・・・
図7左の場合ですと、吸着している高分子が脱落しなければ、重なった部分では高分子の濃度が2倍になります。また図7右の場合にも、吸着層が押し縮められますから、溶媒が搾り出されて、やはり高分子の濃度が高くなります。このように狭い範囲に多くの高分子を押し込んで濃度を高くするには余分なエネルギーが必要で、それだけ分散系全体のエネルギーが高くなりますから、これが反発力につながるのです。図7の2つのパターンのうちどちらが実際に起こるかは状況によって変わって来るでしょう。感覚的には右のへこみ型の方が、ゴムボール(溶媒が搾り出されることを考えると、ゴムボールと言うよりも水を含んだスポンジ)の反発のようなイメージで理解しやすいかもしれませんが、おそらく両方の要素が混ざっている、というのが本当のところではないでしょうか。幸い、どちらのモデルで計算してもさほど大きな違いは出て来ないので、実用上はあまり問題にはなりません。
それでは、電荷による反発の場合と同じように、立体反発の場合のエネルギーの状態を見てみましょう。図8がその例で、円柱型粒子についての計算結果です。
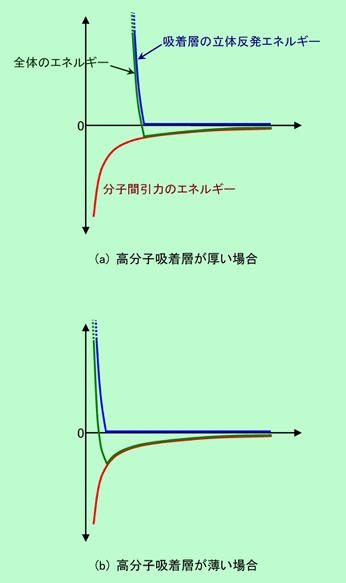
図8 高分子吸着層の立体反発を考慮したエネルギー
立体反発のエネルギーは吸着層が接触しなければ発生しませんから、距離が遠いところ(図の右の方)では完全にゼロです。粒子が接近して吸着層が接触するようになって初めて反発エネルギーが発生するのですが、一旦反発が始まるとエネルギーは一気に上昇することがわかります。粒子が直接に接触するくらいに近付いて来ると、最終的には分子間引力に引きずられて、図4と同じように引力側に落ち込みます。しかし実際にはその前の山があまりに高いために(電荷による反発の場合と比べて、数十倍、数百倍の高さになります)、粒子がこれを越えて接近することはまずありません。というわけで、図ではその部分は省略しています。先に、「高分子の吸着層は硬いプラスティックの殻のようなものではなく、カチンと跳ね返すようなことはない」と書きましたが、実際には吸着層が接触した瞬間に強力な反発力が発揮されていますから、ほとんど「カチン」に近い状態であったわけです。
電荷による反発の場合には、粒子が接近したときに現れる小山の高さが重要でした。これに対して立体反発の場合には、山の高さは問題ありませんから、その手前にできる谷の深さが重要になります。これは、図からすぐにわかるように、立体反発がどこから始まるか、つまり吸着層の厚さがどれくらいかで決まります。図8(a)と比べて吸着層が薄い図8(b)では、引力が十分に強くなってから反発が始まるので、それだけ谷が深くなってしまうのです。このような深い谷に捕まってしまうと、少々かき回したぐらいでは粒子は離れて行ってくれません。吸着層を突き破ってくっ付くまでには至りませんが、吸着層がちょっと接触したぐらいの位置で凝集を起こす、ということになるわけです。それでは、どのくらいの吸着層を作れば、十分に谷を浅くして分散させることができるのでしょうか。これも簡単には言えないのですが、およそ粒子の大きさの5%の厚さ、というのが一つの目安です。もちろん吸着している高分子や溶媒の性質によって状況は大きく変わりますが、例えば直径が0.1μmの粒子の場合、表面に5nmぐらいの厚さの吸着層があれば分散できる可能性が高い、ということです。
とんでもない分散系 ― 磁性粒子 ―
これまでの話では、粒子を凝集させようとする力は分子間力だけでした。しかし、世の中にはさらに強烈な凝集力を持った粒子があります。それが磁性粒子です。磁性粒子とは言っても粒子が十分に小さければ(数十nm)、磁力も大したことはありません。界面活性剤や高分子分散剤を使って分散させることが可能で、磁性流体などが実用化されています。ところが粒子が100nmを超えて来ると、磁力は体積に比例して大きくなりますから、厄介なことになって来ます。その例を図9に示しました。これは同じ円柱型をした磁性を持たない粒子と磁性粒子とのエネルギーを比較したもので、普通の磁気テープなどに使われている磁性粒子の大きさや磁力を参考にして計算したものです。また粒子表面には高分子吸着層が付いていると仮定しています。
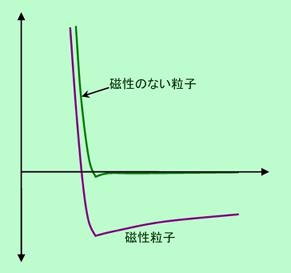
図9 磁性のあるなしでエネルギーはこんなに違う
磁力は分子間力よりもずっと遠い距離まで、しかもかなりの大きさで及びます。その影響で、谷の深さはまさにケタ違い。磁性がない場合の10倍以上の大きさになっています。これだけ谷が深いと、粒子は高分子吸着層を挟んでピッタリとくっ付いてしまい、攪拌程度の力ではとても引き離すことはできません。つまり、このような磁性粒子を安定に分散させることは不可能なのです。しかし、凝集を遅らせることは可能で、後で出て来る軟凝集などを利用した方法などが実際に使われています。いずれにしても、磁性粒子には並みの分散系とは一味違った激しい世界があります。このあたりの詳しい説明は
博士論文の中にもありますから、興味のある方はご覧ください。
凝集の形態
粒子を分散させる話をいろいろとしてきましたが、ここで凝集についても触れておきましょう。一口に「凝集」と言っても、様々な形があります。図10にその典型的なパターンを示しました。
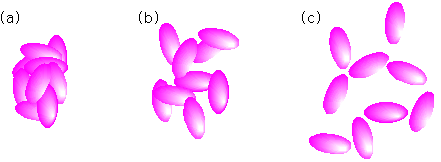
図10 いろいろな凝集の形態
(a)は粒子どうしががっちりと固まった状態で、「凝結(aggregation)」と呼ばれます。こうなると少々かき回したぐらいではほぐれません。これに対して(b)は塊がやや緩く、「凝集(agglomeration)」と呼ばれています。この状態ですと、ある程度強い攪拌操作によって、粒子をばらばらにほぐすことができる場合があります。とは言っても、「凝結」と「凝集」の間に明確な線引きができるわけではなく、かなり曖昧な区別です。英語の辞書を引いても、共に「集団」とか「塊」といった意味で、違いはよくわかりません。ただ実際に分散系を扱う現場では、なんとか解きほぐせる場合を「凝集」、どうやってもほぐれない場合を「凝結」と言っているケースが多いようです。
これらと比べて(c)は少し違っており、「軟凝集(flocculation)」と呼ばれます。「flocculation」を辞書で調べると「綿毛状の塊」とあるように、フワリとした凝集状態で、比較的簡単にほぐすことができる一方、すぐにまた元に戻りやすい、という特徴があります。このタイプの凝集ができると、一般に液の粘度は高くなり、また、急速な沈降が起こって、フワフワしたかさの大きい沈殿物ができやすくなります。ただ、軟凝集が極端に進んで、液全体にわたるネットワークができるような場合には、ゲルに近い状態となり、逆に全く沈降しない、ということも起こります(もっともこの場合には安定に分散しているとは言えず、液全体と同じ体積の沈殿物が初めからできていると見ることもできますが)。これを利用して、凝集しやすく安定な分散がどうしてもできないような系(例えば、先の磁性粒子など)では、わざと軟凝集体を作って凝結に移行するのを遅らせ、分散液の寿命を延ばす、ということも実用上はあり得るのです。
分散系の粘性
液に粒子を分散させると、大抵の場合、粘性は高くなります。それでは、一個一個の粒子がバラバラに分散した時と、凝集がある時とで、どちらが粘性が高いでしょうか? その話をする前に、まず粘性とは何かを簡単に見ておきましょう。
粘性の尺度の基本は文字通り粘度です。粘度というのは、図11に示すように、2枚の板を互いに逆方向にずらす時の抵抗力のことで、その起源は、大雑把に言うと液の成分粒子(液体の分子や溶質、分散粒子)が互いに位置ずれを起こすのに逆らう力です。板のすぐそばの粒子は板にくっ付いて同じ速さで動きますが、板から離れるに従って速度は低下しますから、結果として隣り合う粒子間で速度の差が生じ、互いの位置関係がずれて来ます。これを妨げようとする力が粒子間で働き、粘度として現れるのです。厳密に言うと、速度の速い粒子が速度の遅い粒子にぶつかって後押しし、速度の遅い粒子が速度の速い粒子の動きを邪魔することで、トータルとして速度差をなくす方向に力が働く、ということになるのですが、感覚的には、速度が違う粒子間に働く摩擦力のようなもの、と考えればよいでしょう。この抵抗力は、2枚の板を接近させて速く動かすほど大きくなり、また、板の面積が大きいほど大きくなりますから、当然、これらの条件を単位量にした時の抵抗力として粘度が定義されています。
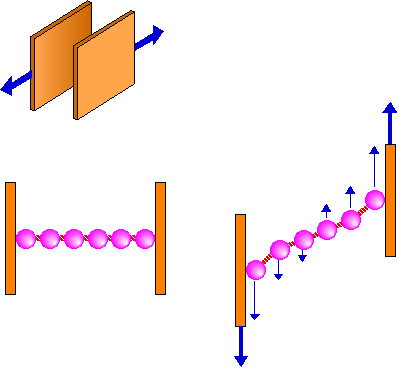
図11 粘性の起源
粒子分散系では、液体分子どうしの他に、液体分子と粒子表面、粒子表面と粒子表面の間にも抵抗力が働きます。これらの抵抗力は液体分子どうしよりも大きいので、分散系の粘度は液体だけの粘度よりも高くなります。もしも粒子どうしの相互作用がなかったら、粒子がどれだけの体積を占めているかだけで分散系の粘性が決まる、ということが理論的に導かれています(ただし、粒子が球形だとか回転楕円体とかの単純な形の場合ですが)。つまり大きい粒子が100個分散していても、その半分の体積の粒子が200個分散していても、液の粘度は同じ、ということです。これはちょっと違和感がありますね。実際に現実の分散系では粒子どうしの作用が大きい場合が多いので、粒子の表面積が大きく、粒子間の距離も近い200個分散系の方が粘度が高くなるのが普通です。非常に乱暴な言い方をすれば、泥水の粘度は高いけれども、砂利入りの水の粘度は高くならない、ということです。
ここで図10(a)のような凝結があるとどうでしょうか。粒子間の相互作用というのはその表面どうしで起こるのですが、凝結すると剥き出しの表面(積)が減ってしまいます。また、凝結した塊どうしの距離は、凝結がない時の粒子間距離よりも遠いですから、粘度は小さくなるのです。これは、先の200個分散系の粒子が2個ずつ凝結して100個分散系に変わったようなものです。
ところが、図10(c)のような軟凝集では話が違ってきます。このようなフワッとした凝集の場合、塊の中にたくさんの隙間があります。ここには溶媒が入っているわけですが、この溶媒は粒子の塊と一緒に動くので、もはや粒子の一部のようなものです。こうなると分散系の中の粒子の量(体積)が増えたのと同じ結果になりますから、液の粘度は上がってしまうのです。さらにこのフワフワ凝集物が液全体にわたるネットワークを作ると、粘度はもっと極端に上昇します。凝集物(ネットワーク)の中の粒子は互いに動けはしますが、その動きに対する抵抗力は、粒子が一個一個バラバラの時よりもはるかに強いので、寒天やゼリーのようなゲル状態に近いものができてしまうのです。
というわけで、分散系の粘度と分散性の関係は、状況に応じていろいろ変化する、というのが初めの問いに対する答になります。また、今回は「粘度」という一言で片付けましたが、実際の分散系の粘性は極めて複雑で、測定条件によって変わりますし、攪拌によって変化したりもします。このあたりの話をし始めると長くなりますので、また別の項に譲ることにしましょう。
雑科学ホーム
hr-inoueホーム