
雑科学ホーム
hr-inoueホーム
● 音の話(その2)●
音は波
物質の振動が波として伝わるのが音の正体で、それが媒質の中や、違う媒質との境目でどのように伝わって行くのか、ということを
音の話(その1)でいろいろ見て来ました。そこでは波としての性質についてはあまり触れませんでしたが、音が見せる様々な現象には、いかにも波らしい、と言えるものがたくさんあります。そこで本稿では、この「いかにも波らしい」音の性質を中心に話を進めることにします。屈折・回折・干渉など、「波動はキライ」という人には聞きたくもない言葉かもしれませんが、音のことを理解する上では避けて通るわけには行きません。人の声や楽器の音なども、波の性質があって初めて成り立つものなのです。
これらの性質は、音だけでなく、電磁波(光や電波)なども含めた波全体に共通するものでもあります。そこで、「音の話」からは外れますが、ところどころで電磁波のことにも触れておきました。光などと対比することで、似たところや違うところなど、音の特徴をよりはっきりさせることができるでしょう。数式抜きの説明ですから厳密さには欠ける部分もありますが、現象としてイメージできると、結構面白いものだと思います。
音も曲がる ― 屈折 ―
性質の異なる媒質が接しているところに波がやって来ると、それぞれの媒質中での速度が違うために進行方向が曲がります。これが「屈折」です。光の屈折については
光学機器の話や
カメラの話にも書いていますが、音についても全く同じ現象が起こるのです。ただし、空気/ガラスとか水/空気とかの間を自由に出入りする光と違って、
音の話(その1)にも書いているように、音は違う媒質の間を移動するのが苦手なので、屈折現象がはっきりと見られるのは、同じ媒質中で場所によって音速が変わるケースに限られます。よく知られている例を図1に示しました。
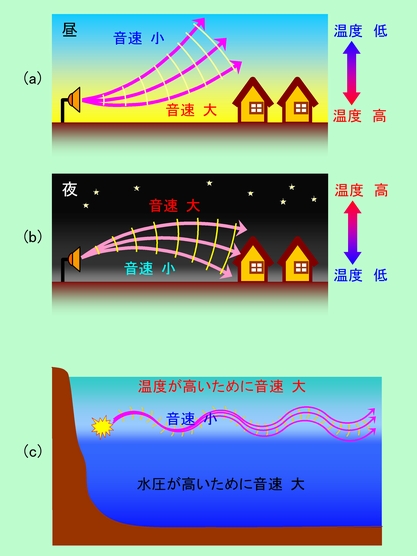
図1 場所によって音速に差があると、音は屈折する
図1(a),(b)は、昼と夜とで音の伝わり方が違う、というもので、これには空気の温度分布が関係しています。晴れた昼間は地面が太陽で温められていますから、地面近くの空気の温度は高く、上空に向かうほど温度は下がります。温度が高いと空気は膨張して密度が小さくなり、それだけ音は速く伝わるようになりますので(
音の話(その1)参照)、地面に近い部分が先に進み、図1(a)のように上に向かって屈折して行きます。音が上空に逃げてしまいますから、地表近くにいる人には、かえって音が届きにくい状態になるのです。逆に夜は地面の方が冷えますから、空気は上に行くほど高温になります。今度は音は下に向かって曲がって行きますので、初め上方に向かって放たれた音も、障害物の少ない上空を進みながら次第に降りて来て、遠くの人にまで届きます。さらに地面で反射して再び上空に向かい、屈折によってまた降りて来る、ということを繰り返し、昼間よりもはるかに遠くまで届くのです。もちろん、昼や夜にいつもこのような状態になるわけではありませんが、傾向として、夜の方が音が遠くまで届きやすい、と言えるのです(夜の方が雑音が少ないという事情もあるでしょうけど)。
空気中だけでなく水中でも、音の屈折で面白い現象が起こります。海の水は、海面近くで温度が高く、深くなるほど冷たくなるのが普通です。暖かい水は膨張して密度が低くなっていますから、上層部ほど音速は大きくなります。一方で、水圧の増加に伴って水の硬さ(弾性率)は増して行きます。そのため、深くなるほど音速が大きくなる、という状況もあります。この両方の影響で、海の中では、水深1000mあたりの音速が最も小さく、それより浅くても深くても音速が大きくなる、という状態ができているのです。そのため、この音速が小さいゾーンで音を出すと、図1(c)のように、浅い方へ向かった音はに下に曲げられ、深い方へ向かった音は上に曲げられます。その結果、音がこのゾーンの中に閉じ込められ、上下に逃げて行くことなく、ずっと遠方まで届くことになるのです。これが海中の「音のチャンネル」と呼ばれるもので、クジラなどはこれを利用して遠くの仲間とコミュニケーションを取っていると言われています。
屈折現象を利用して「音のレンズ」を作ることもできます。例えば、大きな風船の中を二酸化炭素で満たすのです。二酸化炭素は重いので音が遅くなりますから、これがちょうど凸レンズのような働きをして、音を集めることができるのです。逆に水素やヘリウムなどの軽い(音速の大きい)気体を使えば、形は凸レンズなのに凹レンズの働きをする風船を作ることができます。光の場合は、どんな材料を使っても空気中(厳密に言えば真空中)よりも光速を大きくすることができないので、凸レンズ型の凹レンズなどは作れませんが、速度を大きくも小さくもできる音の場合は、こんな芸当も可能なわけです。
ところで、図1(a), (b)と同じような現象が光にも見られることはご存知でしょうか。そう、蜃気楼です。夏の暑い日に、遠くの路面に水が撒かれているように見える「逃げ水」は、地面付近の温度が高いために図1(a)のように光が曲がることで発生する蜃気楼の一種です(光も、空気の温度が高い方が速く進みます)。冬の海などで水温が気温よりも高い状態になった時にも、下の方に暖かい空気層ができて、逆さになった景色が本来の水平線の下側に見えることがあります(空も一緒に下の方に映り込んだりすると、島や船が浮き上がって見える「浮島現象」が起こります)。逆に春から初夏にかけては、海面附近の空気は冷たいのに高いところの空気は暖かい、という状態ができやすく、図1(b)のように光が下向きに曲がって、景色が伸び上がって見えたり、上下がひっくり返った像が空中に浮かんで見えたり、という蜃気楼が現われることがあります。富山湾で有名な蜃気楼はこのタイプです。
音はそこらじゅうではね返る ― 反射 ―
違う媒質に侵入するのが苦手ということは、逆に、反射はしやすいということを意味します。空気中を伝わって来た音が固体にぶつかると、
音の話(その1)の角材の例のように、硬い固体中にはほとんど入り込めず、大部分は反射してしまうのです。固体がゴムのような柔らかいものだと、多少は振動しやすいですから、いくらかは反射の割合が減りますが、それでも大したことはありません。一例を挙げると、空気中の音が鉄に入って行く割合はわずが10万分の1ほどで、ほぼ全部反射します。鉄よりもはるかに軟らかい水の場合ですら、入って行くのは1000分の1に過ぎません。空気中で叫んだ声は、水に潜っている人には1000分の1しか届かないのです。音の強さを表す「dB」で言えば、30dB小さくなる、ということですから、60dBの普通の会話の声が、30dBのささやき声になってしまう、というわけです。
このように、音は固体や液体にぶつかると必ず反射する、と言ってもいいような状況なわけですが、
音の話(その1)にも書いているように、薄い膜状のものや、繊維状のものでは、反射の割合がグッと下がる場合があります。これらのケースでは、音波が固体内に侵入するのではなくて、膜や繊維自体が音を受けて振動を起こし、その結果、音が反対側に抜けて行ったり(正確に言えば、固体の振動が反対側に新たな音波を送り出す)、熱になって吸収されたりして、反射に回るエネルギーが減るのです。いわゆる「吸音材」と呼ばれるのはこのような性質を持つ材料で、グラスウールなどがその代表格です。
いくら吸音材が音を吸収できると言っても、単なる吸音材だけで音の反射を完全になくすのはほとんど不可能です。しかし、本当に反射をゼロに近くできるうまい方法があります。壁を図2のような楔形で埋めるのです。

図2 音を反射しない壁
ここに音がやって来ると、楔形の側面で反射を繰り返して奥へ奥へと進んで行き、元の方向には戻って来ません。しかも奥に向かうほど反射の回数は増え、そのたびに楔の内部に詰められた吸音材でエネルギーを吸収されますから、音が反射して来ることはほとんどないのです。このような壁で内側を埋め尽くしたのが「無響室」で、音に関する精密な測定をする時などに使われます。無響室の中で大声を出しても全く反響がありませんから、室内ではなく野原の真ん中で叫んでいるように感じるそうです。
面白いのは、昔の工場によく見られるノコギリ屋根に、同じような効果があることです。体育館などで声がよく響くことからもわかるように、工場内の騒音が天井で反響すると、うるささが倍増するでしょう。ところが天井がノコギリ型になっていると、図2の楔形と同じように、音が反射しながら屋根の先端に向かって行きますから、下向きに反射する騒音を減らすことができるのです。ノコギリ屋根には、効果的に外の明かりを取り込んだり、空気の循環効率を高めたり、といった働きもありますが、このような防音効果まで備えた、非常に機能的な形だったのです。
無響室の壁が音を反射しないのとよく似た現象が、光にも見られます。縫い針を束ねて先端の方から見ると真っ黒に見えますね。針の先端は円錐形をしていますから、先端側から入って来た光が針の側面で図2と同じような反射を繰り返して奥へ進み、来た方向に全く帰って来ないのです。また、電波を吸収する材料で細長い四角錐を作り、これで壁を埋めた「電波暗室」もあります。無響室の電波版で、これも電波に関するいろいろな実験に使われています。
音の反射で忘れてはならないのが、筒の端っこでの反射です。端が閉じていれば、筒の中を通って来た音がそこで反射するのは当然ですが、筒の先が開いていても反射が起こるのです。ちょっと説明しづらいのですが、思い切り簡略化した図3を使って、その様子を見てみましょう。ここでは筒の中の気体の状態をグッと簡単にして、バネでつながった4個の玉で表してみました。この中に左からピストンで一押し、次いでサッと引いて、縦波を一山だけ送り込みます。
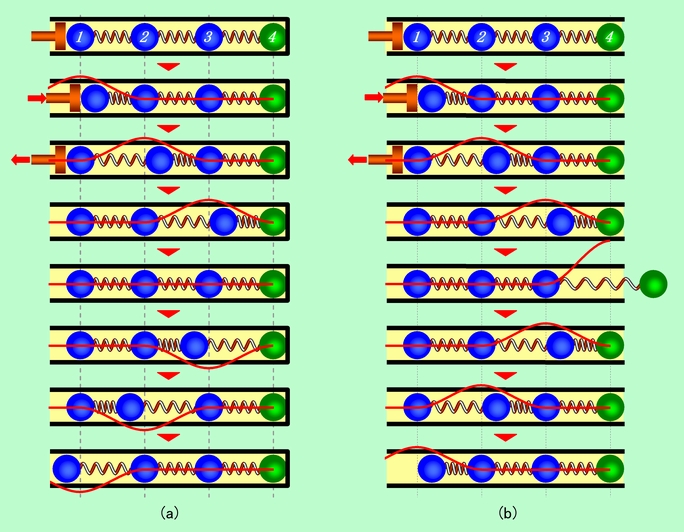
図3 筒先での2種類の反射
図3(a)は筒先が閉じている場合です。まず1番の玉が右に動いてバネを押し縮め、2番の玉に力を伝えます。次の瞬間には押された2番の玉が右に動き(1番は元の位置に戻ります)、同じようにして次々に右への動きが伝わって行きます。そして最終的には筒の端にある4番の緑の玉が右に押されるのですが、すぐ右に壁があって、この玉は動くことができません。その結果、反動で3番の玉が左に押し返されて、今度は左に動くことになります。これが音の反射で、あとは 3番の玉→2番の玉→1番の玉 と左向きの動きが筒内を戻って行くのです。図の中には、赤い線で横波の動きも示しています。これは、玉の動きを、右に動いた場合は上向き(山)、左に動いた場合は下向き(谷)に書き直したものですが、この書き方で言えば、山が左から右に移動し、壁ではね返って、今度は谷になって戻って来た、ということになります。この反射の仕方は、ロープの端をどこかに結び付けて固定し、反対側を上下に振って波を送った時と同じですから、「固定端反射」と呼ばれます。なお、上から5番目の絵で、波が消えたように見えますが、これは「行き」の山と「帰り」の谷が打ち消し合って見えなくなっている状態です。
次は筒先が開いている場合です(図3(b))。今度は右端で筒の内外がつながっているので、外の空気との関係も考えておかなければなりません。筒の中では、ちょっと圧縮しただけで圧力は大きく上昇します。周りが壁で囲まれていて、逃げ場がないからです。ところが筒の端の部分では、外の広い空間につながっていますから、圧力は簡単に開放されて、ほとんど上がりません。そのため、4番の玉が右に動いた時に、それを外から押さえる力は非常に弱くなります。
このような状態にある筒の中に、縦波を一山送ってみましょう。上から4番目までは(a)と全く同じで、4番の緑の玉に右向きの力が伝えられます。すると今度は壁がありませんから、緑の玉は右へ動くことができます。しかも、右から押さえる力が弱いので、それまでの青い玉よりもずっと動きが大きくなるのです。その結果、3番と4番の間には、バネが大きく伸びた(空気の薄い)部分ができ、これに3番と4番の玉が引き寄せられます。3番の立場から言えば、4番が大きく動いた割には(元に戻るのが精一杯で)思ったほど戻って来てくれないので、せっかく元の位置に戻っていた自分が、再び右に引っ張られてしまう、ということです。後は、3番に引っ張られた2番、そして2番に引っ張られた1番と、右への動きが戻って行くことになります。横波で表せば、右端まで来た山が、山のままではね返ったことになるわけです(玉の動きは、行きも帰りも元の位置に対して常に右向きですから)。
逆にピストンを引いて玉を左に動かした場合には、最後の緑の玉は筒の中に大きく引き込まれ、さらに後に続いて(圧力の減少を打ち消そうとして)外の空気がドッと流れ込みます。そのため4番の玉は、大きく左に動いた割には右への戻りは制限され(元に戻るのが精一杯)、代わりに、一旦元の位置に戻っていた3番の青玉が再び左に動かされて、左への動きが筒内を戻って行くのです(谷が谷ではね帰るということです)。これが、ロープの端を固定しない場合に対応する「自由端反射」です。
ここで、玉が密集した(バネが縮んだ)圧力の高い部分と、玉の間隔が開いた(バネが伸びた)圧力の低い部分の位置関係に注目して、もう一度図3をよく見てみましょう。(a)では、高圧部が先に進み、低圧部が後に続いています。反射の後もこの関係は変わりません。ところが(b)では、反射した後は低圧部が先行しています。反射のところで順番がひっくり返っているのです。このことは、
音の話(その1)で説明している、縦波を横波で表す2通りの方法で音の反射を描いてみれば、いっそうよくわかります。その2通りの方法とは、「玉の前後(図では左右方向)の動きを上下方向に描き直す方法(変位表示)」と、「圧力を上下方向に表示する方法(圧力表示)」です(図4)。
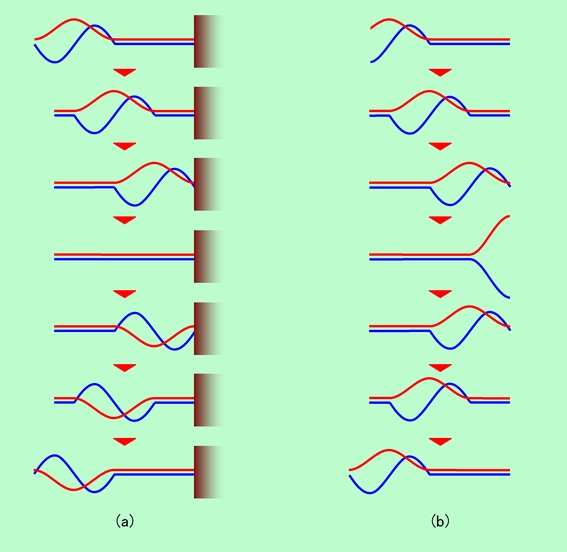
図4 筒先での反射を2通りの横波表示で表す
赤線は図3と同じ変位表示で描いたもの、青線は圧力表示で描いたものです。変位表示(赤線)では、(a)の固定端反射の時に山と谷が反転し、(b)の自由端反射では反転しないのに対して、圧力表示(青線)では逆に、(a)の固定端反射の時に反転が起こらず、(b)の自由端反射で反転しています。一見奇妙に見えるかもしれませんが、これ自体は同じ現象を違う視点から見ただけのことであり、不思議なことでも何でもありません。圧力の立場で見ると、開いた筒先では圧力は変化できない(外の圧力に固定されている)わけですから「固定端」的な反射を、閉じた筒先では圧力が変化できますから「自由端」的な反射を起こす、と考えることもできるのです。ただし、この2種類の表示方法をしっかりと区別しておかないと、後に出て来る「音の干渉」のところで混乱することになりますから注意が必要です。
なお、図では開いた筒先できっちりと反射が起こるように描いていますが、実際にはもう少し複雑であることを付け加えておきます。圧力の状況が出口ですぐに変わるわけではなく、少し出たところまで内部の影響が及ぶために、反射位置は出口よりも少し外側になるのです(開口端補正)。
ところで、自由端の反射は、筒の出口で圧力が急激に開放される(急に外と同じ圧力になる)ことで発生していました。と言うことは、この変化を少なくしてやれば反射を減らせる、ということになります。そのためには、急にスパッと筒を切るのではなく、徐々に広がる形にしてやればよいのです。こうすることで筒先での急激な状況変化がなくなり(図3で言えば、緑玉の動きが青玉と比べて極端に違う、ということがなくなり)、音が効率よく外に出て来ることになります。これが、メガホンが円筒ではなく円錐形になっている理由です。伝声管の口や、トランペットやクラリネットなどの楽器の先端がアサガオ型に広がっているのも、音の出をよくする工夫なのです。
音が回り込む ― 回折 ―
波が障害物の陰に回りこむ現象が「回折」です。これまた光の回折については、
光学機器の話や
カメラの話、さらには
顕微鏡の話などにも頻繁に登場しますから、詳しい話は省略しますが、重要なのは音の波長が結構長い、ということです。例えば440Hzの音の波長は、空気中では80cm近くもあります。これは光で言えばテレビのUHF放送や携帯電話に使われる極超短波の領域で(
発光の話参照)、可視光線と比べれば100万倍も長いのです。波長が長いほど波は回折を起こしやすいですから、光にとっては完全に陰になるような部分にも、音は平気で回り込む、ということになります。逆にこの現象がなかったら、ずいぶん不便なことになるでしょう。建物の陰から近付く車の音は全く聞こえなくなってしまいますし、パーティションの向こうにいる人を呼び出すこともできません。このように考えて行くと、光で見ることができない部分の情報を得るのに、音がいかに有効であるかがよくわかりますね。
音の重ね合わせ ― 干渉 ―
2つの波が出逢った時、山どうし、谷どうしが重なれば強め合い、山と谷が重なれば弱め合います。これが波の「干渉」で、音波ももちろん干渉を起こします。ただし、世の中を飛び交っている音の波形は非常に複雑ですから、はっきりした干渉を実感する機会は少ないかもしれません。その中で、比較的わかりやすいのは「うなり」と「定在波」でしょう。
うなり
「うなり」は、周波数が違う音が重なった時に、その差に相当する周波数で振幅が波打つ現象です。ゴチャゴチャ説明するよりも、実際の波形を見た方が早そうですね。
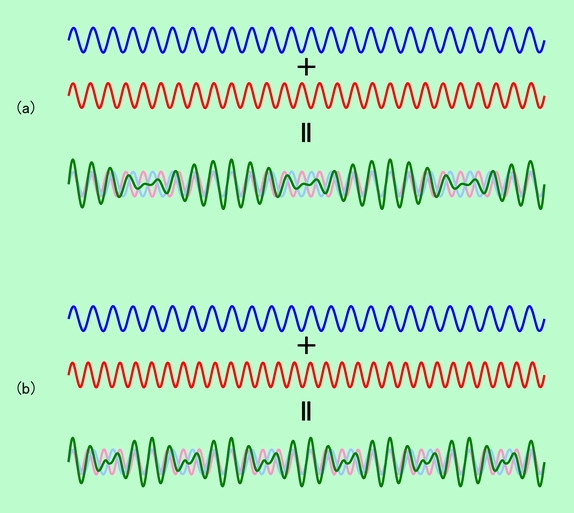
図5 周波数の違う波が出逢うと「うなる」
図5(a)では、青の波は、この図の範囲で24回振動しています。一方、赤の波は27回振動していますから、その差は3回。この2つを足し合わせると、緑線で示したように、ちょうど3回大きくなったり小さくなったりを繰り返す波ができます。同じように(b)では、青波は同じですが、赤波が29回振動していますから、その差は5回で、5回増減を繰り返す波ができるのです。実際の例では、例えば周波数440Hzの音と442Hzの音を同時に流すと、1秒間に2回、つまり2Hzでウァンウァンとうなる音が聞こえます。
うなりを使うと、わずか1Hzや2Hzの違いが敏感に検出できますから、楽器などで音の周波数を正確に合わせるのに利用されます。逆に2つの音の周波数が違い過ぎると、うなりはよくわからなくなってしまいます。例えば440Hzの音と300Hzの音を混ぜると140Hzのうなりが聞こえるはずですが、周波数が大きすぎて音の大小の変化を感じ取ることはできず、雑音が混じっているように聞こえてしまうのです。
音のうなりと同じように、周波数の違う光を重ねると、その差の周波数で強度が変化するのが見られます。「ヘテロダイン干渉」と呼ばれる現象で、元々は電波を増幅して微弱な信号を取り出すのに使われていました。最近では、波長がキッチリ決まった干渉性のよい光、レーザーが発達していますから、電波ではなくて、もっと波長の短い可視光線でも同じ現象が扱えるようになっています。
これとは別に、波が干渉しているわけではありませんが、原理的に「うなり」と同じ仕組みで現われる現象に、図6に示した「モアレ」があります。この図のように、ピッチの違う格子模様を重ねると、それよりもはるかに長いピッチの太い縞模様が現われるのです。縞の位置が少しずつズレて行き、ちょうど縞模様一つ分だけズレて再びピッタリ重なるまでが、モアレの一周期になります。
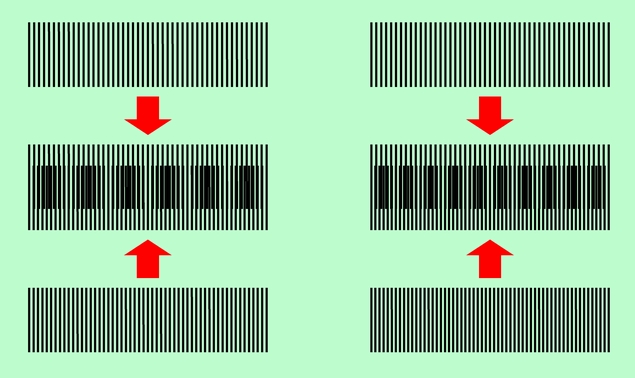
図6 「うなり」と同じ原理で発生する「モアレ」
このようなモアレは、ピッチの違う格子を重ねた時だけではなく、同じピッチの格子を斜めに重ねた時にも現われますし、孔をたくさん開けたメッシュ状の物でも見られます。2枚の簾が重なった時や、2重になった橋の欄干などで目にすることがあると思います。うなりを理解するのにちょうどよいモデル、と言えるかもしれません。
定在波(定常波)
定在波(定常波)は、もう一つの典型的な干渉現象です。別の方向から来た同じ波長の2つの波が重なって、常に大きく振動している部分(腹)と、全く振動しない部分(節)ができるもので、波が進行せずに止まって見えるので「定在波」と呼ばれます。2つの波が図7のようなきれいな形で、しかも振幅が全く同じ場合には、完全な定在波ができます。腹と腹(節と節)の距離は元の波の波長の半分、腹の部分の振幅は元の波の2倍、節の部分の振幅は完全にゼロになります(赤と青の波が重なってできた緑の波が定在波です)。なお、元の波の形が違っていると、当然、完全な定在波にはなりません。また、形が同じであっても振幅が違っていると、振幅の大きい方に引きずられて、「定在」せずに少しずつ移動する波になります。
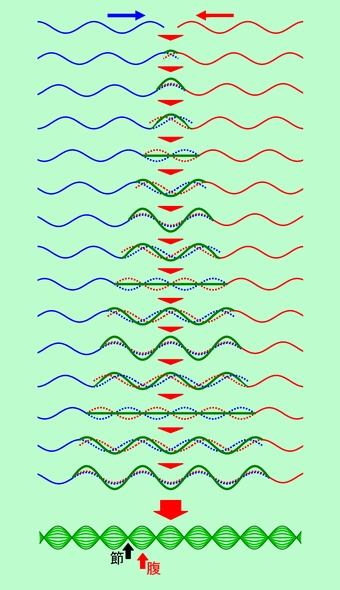
図7 「腹」と「節」ができる定在波
2つのスピーカーから同じ音を出した場合、スピーカーの間では両方からの音波がぶつかって定在波ができます。定在波の腹の部分では振動が大きいので大きな音が聞こえ、節の部分では音が聞こえない・・・・ならば話は簡単ですが、実はそう単純には行きません。「腹」「節」という考え方は横波には都合がよいのですが、音のような縦波に対して使う時には注意が必要です。
図8上の図のように、左右のスピーカーから同じ音を出したとします。「同じ音」ということは、左のスピーカーが空気を押した時には右のスピーカーも押し、左が引いた時には右も引く、ということを意味します。ここで、縦波を横波で表す2つの方法があったことを思い出してください。まず一つ目の「変位表示」ですが、「右への動きを上に取る」と約束すると、左のスピーカーが空気を押した時に送り出されるのは「山」になります。ところが、右のスピーカーが空気を押した時には、空気は左に動かされますから、送り出されるのは「谷」です。つまり左から「山」が来た時、右からは「谷」が来るのです。その結果、定在波の形は(a)のようになります。何と、中央部は「節」になるのです。
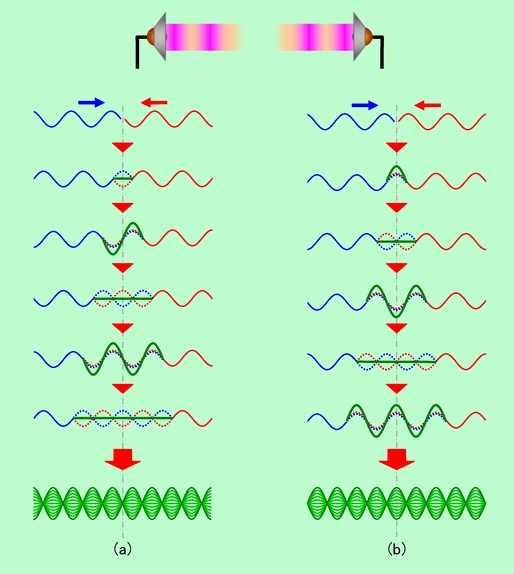
図8 音の定在波はちょっとややこしい
それでは二つ目の「圧力表示」ではどうでしょうか。今度は左のスピーカーが空気を押して「山」を送り出した時には、右のスピーカーも同じように「山」を送り出すことになります。そのため定在波は(b)のように、中央部が「腹」になる形になります。このように、2つの方法で定在波の腹や節の位置が全く逆になってしまうのです。
なぜこのようなことが起こるのかを、少し考えてみましょう。2つのスピーカーの中央部に注目してください。ここにある空気は、両側から同時に押されたり、同時に引っ張られたりします。押す力も引っ張る力も左右で全く同じですから、結局ここの空気は動くことができません。動きがないのですから、「左右の動きを上下方向に描き直す方法」で横波表示した時には、当然ゼロの位置に来ることになり、定在波としては「節」になるのです。しかし、動きがないからといって、この部分が何の変化もない平穏な場所、というわけでは決してありません。確かにど真ん中は動きませんが、その両側はグッと近寄って来たり、遠くに離れて行ったりしますので、圧力は非常に激しく変動しています。そのため「圧力を上下に表示する」方法では、ここが最も激しく変化する「腹」となるのです。
それでは音が大きく聞こえるのはどこか、ということですが、人の耳でもマイクロフォンでも、圧力の変化を音の大きさとして捉えるようにできていますから、音が一番大きいのは、変位表示ならば「節」の部分、圧力表示ならば「腹」の部分ということになります。感覚的には「腹の部分で音が大きくなる」という方がしっくり来ますよね。その意味では、音の干渉を扱う場合には、普通の変位表示よりも圧力表示の方が便利なように思います。もちろん、きちんと理解して使いさえすればどちらでもよいわけですが・・・・。
ついでに、2次元平面での波の干渉の様子も図9に示しておきました。今までの直線上の波の場合には変位の方向は右か左かのどちらかに決まっていましたから、これを上下に焼き直せば横波表示ができました。しかし2次元平面の場合には、変位の方向が360度あらゆる方向になりますので、簡単に横波表示することができません。そこで図9では、単に圧力の大きさだけを示せばよい「圧力表示」を使って、各点での圧力を色の違いで表現しています。赤色の濃い部分が圧力が高い「山」、青色が濃い部分が圧力の低い「谷」です。左右の黒い点が音の発生源で、そこから同心円状に波が拡がって行きます。
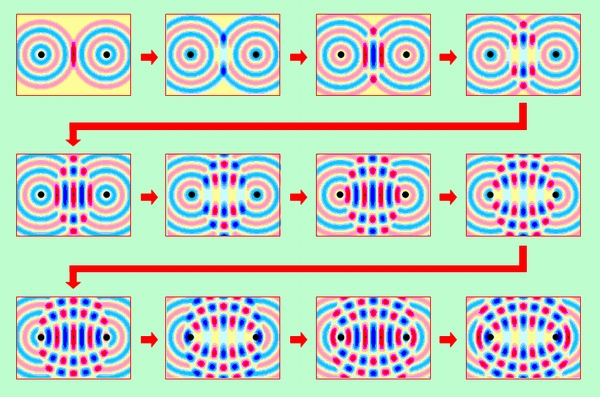
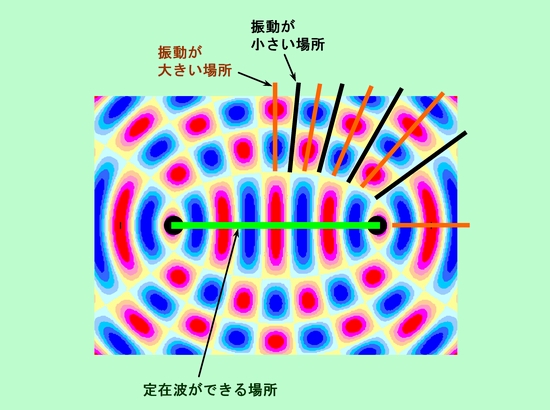
図9 2次元平面での波の干渉
音の発生源を結んだ直線上(下の拡大図の緑の直線部分)は、図8(b)と全く同じ状況ですから、ここには定在波ができます。時間変化を追って行けば、赤(山)→黄(ゼロ)→青(谷)→黄→・・・・、と大きく振れて腹になっている部分と、黄色のままで全く振動していない節の部分が交互に並んでいることがわかると思います。一方、この線を外れた部分では、山や谷は「定在」することができず、常に進行しています。しかし、振動の激しい部分と、ほとんど振動しない部分ははっきりと分かれていて、拡大図の橙色の線上では、山や谷が時間と共に次々に通過して行くのに対して、黒線で示した部分は常に振動がゼロで、定在波の節と同じような状況になっています。当然、橙色の線上では音が重なって大きく聞こえ、黒色の線上では音がほとんど聞こえない、という状態になるのです(もちろん、複雑な波形の音の場合には、完全に打ち消されてしまうことはなく、何らかの音が残りますが)。これは、
立体映像の話や
カメラの話で示した光の干渉と全く同じ状況ですね。なお、この図で示したのは、音源の距離がちょうど波長の整数倍になっている場合のバターンですが、距離が変わると少し様子が違って来ます。例えば、あと1/2波長分だけ距離が離れる(または近付く)と、音源の外側を真横に走る橙色の線は黒線(振動しない場所)になります。
ここまでは、左右から別の音が送られて来る形で定在波の説明をして来ましたが、一つの音がはね返る場合にも、行きの波と帰りの波が干渉して定在波ができます。図10はその様子を変位表示で示したもので、(a)は固定端反射、(b)は自由端反射の場合です。(a)では反射面が節になり、(b)では反射面が腹になることがわかると思います(圧力表示の場合は、固定端反射が(b)のパターン、自由端反射が(a)のパターンになります)。
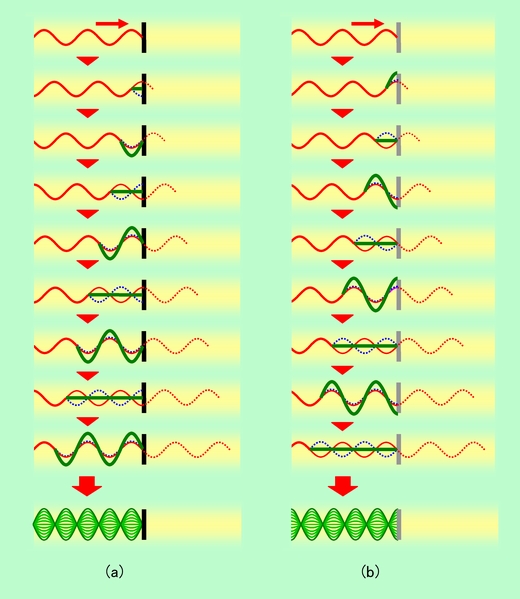
図10 反射が作る定在波
このような作図をする時によく間違えることがあるのですが、コツを押さえてしまえば簡単です。まず初めに、反射面を無視して波をそのまま延長し(赤の破線)、それを反射面で折り返します(青の破線)。この時、自由端反射ならばそのまま折り返し、固定端反射ならば上下をひっくり返して折り返せばよいのです(圧力表示の場合は逆)。あとは、折り返した波と元の波を足し合わせれば完成です。自由端反射の反射面では、足し合わせることで振れが常に2倍になりますから、ここは腹。一方、固定端反射の反射面では、大きさが同じで向きが逆の波の足し算になりますから、振動は常にゼロで、ここは節になるのです。
音を重ね合わせて強める ― 共鳴 ―
音が一回反射するだけならば、図10のように行きと帰りがすれ違う場所で一瞬定在波ができるだけですが、箱や筒のように両側で反射する構造になっていると、音が往復して何度も干渉できるようになります。この時、山や谷が出会う場所が毎回違っていると、腹や節の位置が一定せず、やがて平らにならされて消えてしまうでしょう。しかし、箱や筒の大きさを音にうまく合わせて、必ず同じ場所で山や谷が出会うようにしてやれば、腹や節の位置が固定された安定な定在波を作ることができます。逆に言えば、箱や筒の大きさが決まれば、その中で定在波ができる音の周波数(波長)も決まる、ということで、これを、その箱や筒の「固有周波数」と呼びます。固有周波数にピッタリ合った音が入って来ると、内部に安定な定在波ができ、続けて入って来る音が、この定在波にどんどん重なって振動が大きくなって行きます。ちょうど、ブランコをタイミングよく押してやれば、どんどん揺れ幅が大きくなって行くのと同じような現象ですね。これが音の共鳴です。
共鳴は、何も箱や筒の中の空気の振動に限ったものではありません。振動する物体には必ず、定在波ができる固有周波数があり、それがちょうど人間が聞くことができる音の領域にあれば、音に反応して共鳴を起こします。また、その物質を叩いた時には、定在波ができる振動だけが長時間生き残りますから、固有周波数に対応した音が出ることになります。一般的に、その物質が硬いほど、またサイズが小さいほど、固有周波数は大きくなり、高い音に反応するようになります。例えば、10cmぐらいの金属の塊なら数kHz、もっと小さい金属やセラミックス類では超音波の領域に入って来ることもあります。また、形も重要な要素で、薄い板状や細い棒状になれば、固有周波数はずっと下がります。楽器の調律などで使われる音叉では、形や大きさ、材質などを調整して、きっちりと狙った周波数の定在波ができるようになっているのです。
固有周波数による共鳴現象を実験で確かめる方法の一つは、同じ固有周波数を持った物を2つ並べて一方を叩く、というものです。物を叩くと、先に書いたように固有周波数で振動する定在波ができて、その高さの音が強く出ます。すると、その音にもう一方が共鳴し、直接触れていないのに同じ周波数で振動を始めます。普通の物質では音の減衰が早すぎて、なかなかこの現象を捕まえることは難しいのですが、音叉のように長時間安定に音を出すものならば、簡単に実験することができます。
先に出て来た箱や筒も、共鳴現象を調べるのによく使われます。振動するのは箱や筒自体ではなく、その中の空気ですから、これは「気柱」と呼ばれています。気柱の中にできる定在波の様子を図11に示しました。(a)は筒先の片方が閉じている場合、(b)は両方が開いている場合で、音の波を変位表示で表しています。
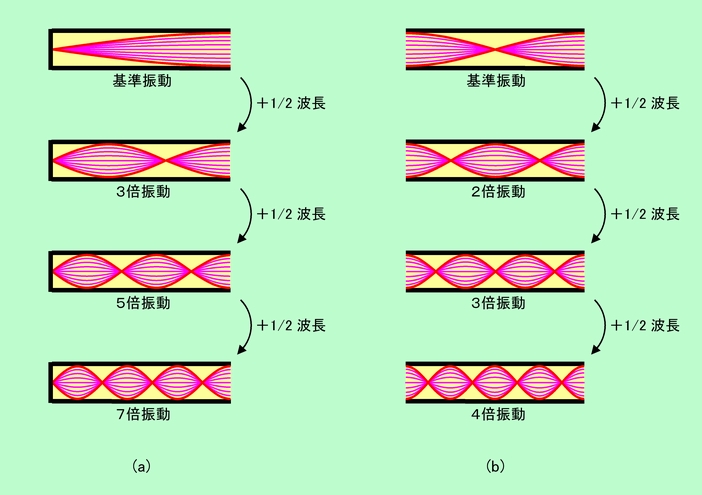
図11 気柱の中にできる定在波
図11(a)の場合、開いている側は自由端反射、閉じている側は固定端反射ですから、それぞれが必ず(変位表示の)腹と節になります。右端を腹にした波と左端を節にした波ができるわけですが、この両者がピッタリ重ならなければ定在波にはなりません。このような条件を満たす最も簡単な状態が、図11(a)の一番上に示した、気柱の長さがちょうど1/4波長になる場合です。これを基準振動と言い、あとは周波数がこれの3倍、5倍、7倍・・・・(波長で言えば、1/3、1/5、1/7・・・・)という奇数倍の周波数を持つ音で定在波ができることになります。同じように、両端が開いている図11(b)の場合には、両端が腹にならなければなりません。これを満たす基準振動は、図の一番上に示したように、気柱が波長の1/2の長さになる場合です。そして基準振動の2倍、3倍、4倍・・・・という整数倍の周波数を持つ音だけが、気柱の中に定在波を作ることができます。
(a)の場合は基準振動の奇数倍なのに(b)の場合は整数倍、というのは妙な感じがするかもしれません。しかし、基準振動の場合の気柱の中の波が、(a)では1/4波長であるのに対して(b)では1/2波長なのですから、このような違うものを基準にすれば、倍数が変わって来るのは当然です。気柱の中のうねりの数を数えてみれば、どちらも全く同じように1/2波長(節から節までのひと塊)ずつ増えていることがわかると思います。
この気柱の共鳴現象を利用しているのが、様々な楽器です。パイプオルガンやトロンボーンなどは、管の長さを変えることで音程を変えていますが、これは正に、気柱の長さを変えて基準振動の周波数を変化させているのです。フルートやクラリネットなどでは、管の側面に開けた孔を塞いだり開いたりして音程を変えるので、単純な長さの変化とは違いますが、やはり共鳴する周波数を変えていることに違いはありません。
ダックボイスの謎
ヘリウムを吸い込むと、声が高くなってアヒルのように聞こえる「ダックボイス」。テレビなどでもよく紹介されますから、見たことがある人も多いでしょう。この現象は、「ヘリウム中では音速が大きいので、声の周波数が高くなる」というふうに説明されることが多いのですが、これで納得できますか? 確かにヘリウム中では、音は速くなります(
音の話(その1))。しかし、音が口から外に出てしまえば、そこは普通の空気ですから、聞き手に届く時には音速は元に戻ってしまいますし、そもそも音速が大きくなるだけならば周波数(つまり音の高さ)は変わらないはずです。これはいったい、どういうことでしょうか。実は「ダックボイス」は、人間が声を出す仕組みと深く関わっているのです。
人間の声が「声帯」で作られることはご存知でしょう。声帯は喉の奥にある門のような器官で、これが閉じることで空気の通り道を狭めます。吐く息がこの狭い隙間を通過する時に声帯を震わせ、声の元が作られるのです。ただし、ここで作られるのは単なる「声の元」であって、普段聞いている声とは似ても似つかない、「ブー」という感じの弱々しい「音」に過ぎません。これを喉や口や鼻が作る空間で複雑に共鳴させることで大きな音に変え、さらに必要に応じて唇や舌などを使って作られる子音と組合わせることで、ようやく声が完成します。喉や口の中の状態を微妙に変化させると、共鳴する音の周波数が変わりますから、それによって声に含まれる周波数の成分が変化し、様々な高さ、様々な音色の声を出すことができるのです。
以上のことを頭に入れた上で、もう一度ダックボイスのことを考えてみましょう。ヘリウムを吸い込むと、喉や口の中がヘリウムで満たされます。もちろん、100%のヘリウムを吸い込むと酸欠で倒れてしまいますから、実際に試す時には20%程度の酸素を含んだヘリウムを使います。この気体の中の音速は約870m/sで、空気中の2.5倍ぐらいになります。この状況で、空気中と同じように声帯を震わせてみましょう。空気中でもヘリウム中でも、声帯の振動自体に大きな変化はありません(気体の粘性などが若干違うので、多少は違いがあるかもしれませんが)。ところが、この「声の元」を共鳴させる段階になると、大きな差が出て来ます。
音速が大きいヘリウム中では、一回振動する間に遠くまで音が進みますから、同じ周波数ならば波長が長くなります。逆に言えば、同じ波長ならばヘリウム中の方が周波数が高い、ということになります。ここで、図11の気柱の共鳴を思い出してみましょう。決まった長さの気柱では、決まった波長の音だけが共鳴していました。ということは、喉や口の中の状態が同じならば、ヘリウム中の方が、より周波数の大きい、つまり高い音が共鳴することになります。音速が2.5倍ですから、共鳴する音の周波数も2.5倍、ということで、ヘリウム中の方が1オクターブ以上も声が高くなるのです。これがダックボイスの正体です。
ここまで来ると、声に限らず、ヘリウム中で音が高くなるものと、ならないものとがあることに気が付きます。気柱の共鳴を利用しているものは音が高くなり、利用していないものは高くならないのです。クラリネットやフルートなどの木管楽器、トランペットやトロンボーンなどの金管楽器は気柱そのものですから、当然、ヘリウム中で音が高くなるはずです。これに対してシンバルや太鼓などの打楽器は、それ自身の振動で音の高さが決まりますから、ヘリウム中でも変化はありません。ただし、太鼓の胴体が共鳴器の役割を果たしている場合には変化が起こる可能性はありますし、音色や音の大きさも違って来るでしょう。同じことがバイオリンなどの弦楽器にも言えて、音の高さを決める弦の振動数には変化がありませんが、胴体での共鳴にはいくらか影響が出るはずです。おそらく空気中で最もよい音が出るように設計されているでしょうから、ヘリウム中では音質が悪く、音も小さくなるのではないでしょうか。
通過する救急車の音 ― ドップラー効果 ―
音の話の最後に、「ドップラー効果」のことに触れておきましょう。「ドップラー」というのは、この現象を予測したオーストリアの物理学者Dopplerのことで、「目の前を通過する救急車のサイレンの音が、近付いて来る時には高く、遠ざかって行く時には低く変化する」ことで有名な現象です。原理的には簡単なもので、図12のように、音を出しながら動く物の前側では音の波が圧縮され、後ろ側では引き伸ばされることによって発生します。
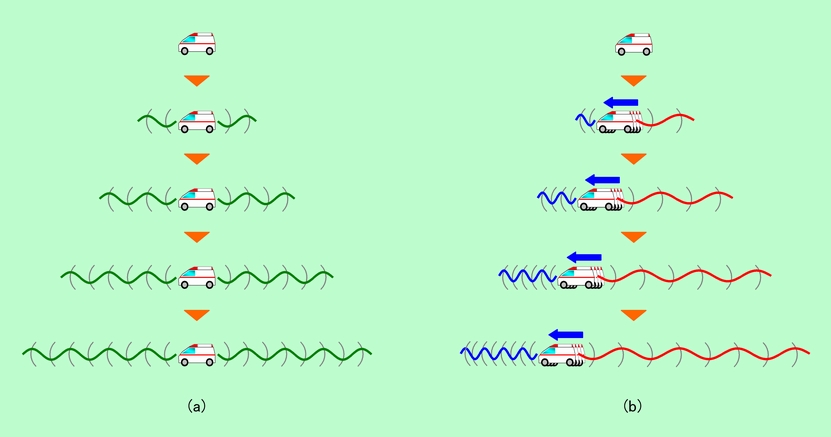
図12 圧縮される波と引き伸ばされる波・・・ドップラー効果
救急車が止まっている場合には、図12(a)のように、音は前にも後ろにも同じように拡がって行きます。ところが(b)のように救急車が動いている場合、救急車の中から見ると、前方に出た音は救急車が後を追っている分だけ遅く見え、後方に出た音は、救急車がどんどん離れて行くために速く見えます。その結果、救急車からは常に同じ周波数の音が出ているにもかかわらず、前方では音がギュッと圧縮されて波長が短くなり、後方では引き伸ばされて波長が長くなることになります。一方、救急車の外の人から見ると、前の音も後ろの音も速度は同じですから、波長の短い前側の音は周波数が高く、波長の長い後ろ側の音は周波数が低く聞こえます。つまり、救急車の前方では音が高く、後方では低く聞こえることになるのです。
図12では音源の方が動いていましたが、音源が止まっていて、聞く側が動いている場合にも、同じような現象が起こります。例えば、聞き手が音源に近付いて行く場合、止まっているよりも速いテンポで波を受け取ることになりますから、音は高く聞こえるのです。また、動いている物に音をぶつけて、その反射音を捉える場合には、両方の効果がダブルで効いて来ます。近付いて来る物体に音がぶつかる時に元よりも少し高い音になり、さらにそこから放出される反射音は、図12の効果でもう一段高くなるのです。
これを利用すると、音波を使って物体の速度を測ることができそうです。ところが、音は狙った方向に真っ直ぐ進むわけではなく、大きく拡がってしまいますし、温度や風、別の音などの外乱も受けやすいですから、超音波を使った一部の例を除いては、速度計測にはあまり使われません。その代わり、電磁波(光や電波)の世界では、ドップラー効果は大活躍しています。野球でおなじみのスピードガンや、車のスピード違反を取り締まる速度計などは、電波の反射によるドップラー効果を利用しています。また「ドップラーレーダー」という名前を聞いたことがある人もいるでしょう。普通のレーダーは電磁波の反射を捕まえて物のあるなしを判定するだけですが、このレーダーは反射波の周波数変化を計測して、対象物の動きを調べることができ、気象観測などで使われています。天体観測では、星からの光がドップラー効果を起こして波長(つまり色)が変わるのを利用して、その星が遠ざかるスピードを測ったりしています。宇宙の膨張が見えるわけですね。
ドップラー効果による周波数の変化は、元の波の速度と物体の速度とが近いほど大きくなります。その意味では、音よりも百万倍も速い電磁波で周波数の変化を測るのは難しそうですね。星のように猛スピードで動いている物ならともかく、野球の投球や車の速度はせいぜい40m/sぐらいのものですから、光の速度と比べれば1千万分の1程度。ということは、周波数の変化も1千万分の1しかない、ということです。そこで実際の測定器では、干渉現象を利用して、わずかな周波数の変化でも捉えられるように工夫がされています。例えば、元の電磁波と反射して来た電磁波とを重ね合わせて図5の「うなり」を起こさせれば、わずかな周波数の違いを簡単に捕まえることができるのです。
ところで、物体の速度がさらに大きくなって、音速を超えてしまったらどうなるのでしょうか。電磁波ではこの心配はありませんが、速度340m/sの音ならば、「超音速」はそう珍しいことではありません。図12の救急車を飛行機に替えて、そのパターンを示したのが図13です。
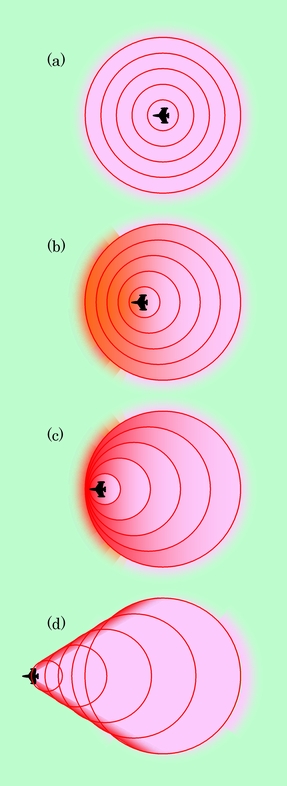
図13 「超音速」になると、音が置いて行かれる
止まっている場合は、図13(a)のように、音は四方八方に均等に拡がって行きますが、飛行機が動くと、(b)のように、前側では音の波が圧縮され、後ろ側では引き伸ばされます。これは図12と同じ、普通のドップラー効果です。飛行機がさらに速くなって、ほとんど音速と同じになると、(c)のように前方での音の圧縮は極限状態になります。波が非常に狭い範囲に押し込まれ、壁のようになるのです。これが「音の壁」で、この端の方が地上に届くと、強烈な爆音として聞こえることになります。そして飛行機の速度がさらに増して音速を超えた瞬間、音の壁は突き破られ、飛行機は(d)のように、自身が出した音を遥か後方に置き去りにするのです。この時、圧縮されていた空気が急激に開放されて温度が下がり、飛行機の周辺に円錐状の雲が発生することがあります。この雲が発生すると、本当に飛行機が壁を突き破ったように見えます。
音速を超えると、飛行機には自分が出した音はもう届きません。しかし、後ろの方ではやっかいな状態になっています。音の拡がる領域は図13(d)のような円錐状(マッハコーンと呼ばれます)になるのですが、この円錐の側面の部分では、音の波の間隔が非常に狭くなっていることがわかると思います。つまり、音の壁と同じように、この部分には大量の音が詰め込まれて強烈な衝撃波ができているのです。これが爆音として地上に届いたのが、超音速飛行機が作り出す「ソニックブーム(Sonic Boom)」で、実際にガラスが割れるなどの被害が出たこともあるそうです。普通の音の圧力などは微々たるものなのですが、目いっぱい集中させると、このような大きな威力を見せるのです。
雑科学ホーム
hr-inoueホーム














