
雑科学ホーム
hr-inoueホーム
● カメラの話 ●
"カメラ"の元の意味は"部屋"
「カメラ(Camera)」と言えばもちろん写真を撮るための道具ですが、その語源はラテン語の「カメラ・オブスキュラ(camera obscura)」で、「camera」は「部屋」、「obscura」は「暗い」という意味です。つまり「暗い部屋」。「なんのこっちゃ」という感じですが、実は「camera obscura」は単なる「暗い部屋」ではありません。その正体は、部屋の壁に小さな孔を開けて外の景色を反対側の壁に映す投影機であり、正確な絵を描くための道具として数百年前から使われていました。後になって、この映った像を記録する技術が発明され、「camera obscura」の前半だけを取って「camera」と呼ばれるようになったのだそうです。「裁縫をする機械」=「sewing machine」の後ろ半分だけを取って「ミシン」と呼ばれるようになったのと同じような感じですね(これは日本だけの話ですが)。今でもカメラは周囲の光が入らないようにしっかり囲まれた小さな部屋であることに変わりはありませんから、「カメラ」=「部屋」という図式は、それほど大きく外れたものではない、と言えるかもしれません。
カメラ・オブスキュラでは映った像を人間の手でなぞって絵にしていたのですから、まだ今で言う「カメラ」とは違います。映った像を自動的に記録する技術がセットになって初めて“カメラ”と呼べるシステムになるわけで、その記録のために、光が当たると変色する薬剤がいろいろと研究されました。銀の化合物やらアスファルトやらが試された記録が残されていますが、感度が低かったり画質が悪かったり保存性が悪かったりで、一般に普及する物はなかなかできなかったようです。そんな中で、
光学機器の話にも書いているように、1839年にフランスのダゲールがダゲレオタイプを発明します。感光剤の成分や現像の方法などは現在のものとはかなり違いますが、曲がりなりにもそこそこの解像度で、そこそこ鮮明な、ある程度保存も利く写真が撮れるようになったのです。その後のカメラの隆盛は言うまでもありません。望遠鏡や顕微鏡はなくても、カメラはたいていの家にはあるでしょう。携帯電話に付属するカメラも含めれば、その数は相当なもの。今や最も普及した光学器械、と言えそうです。
このように、カメラには「像を形成する部分」と「像を記録する部分」の2つの要素があります。像の記録、特にフィルムに関しては、化学の要素がたくさん含まれていて、それはそれで非常に面白いテーマなのですが、ほとんどがデジタルカメラに換わりつつある状況もあり、今回は「像を形成する光学器械」としてのカメラを中心に話を進めることにしました。簡単な原理などは
光学機器の話にも書いていますので、ここではもう少し詳しい話やトピックス的な話題を取り上げることにします。
基本はピンホール・カメラ
初期のカメラ・オブスキュラもそうですが、カメラの基本はやはりピンホール・カメラでしょう。レンズの代わりに小さな孔(ピンホール)が開いた単純な構造ですが、屋外の風景などは意外にきれいに撮れて驚かされます。もちろんレンズを使ったカメラと比べて取り込める光の量はずっと少ないですから、撮影に長い時間がかかるのは仕方がありません。
ピンホール・カメラの原理は説明するまでもないと思いますが、一応、簡単に示しておきましょう。
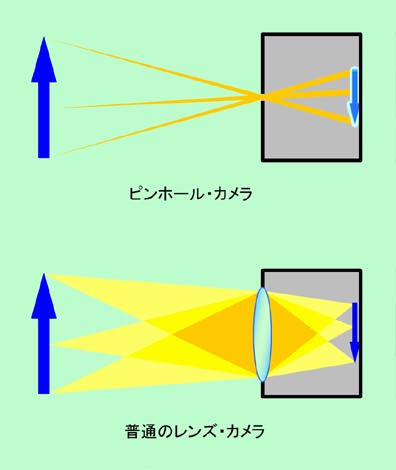
図1 ピンホール・カメラはボケた点の集まりで像を作る
図1の上側に示したように、景色の一点から出た光は四方八方に拡がりますが、そのうちのごく一部がピンホールを通り抜けてフィルムや受光素子(あるいはオモチャの場合はスリガラスかも)に届きます。この時ピンホールが十分に小さければ、受光面でもそれほど大きな拡がりにはならず、「少しボケた点」ぐらいにとどまるでしょう。撮影対象が十分に遠ければ光は平行光線に近くなりますから、「ボケ」の大きさはピンホールの直径とほとんど同じ程度になるはずです。ピンホール・カメラでは、このような「ボケた点」を寄せ集めて像を作るのです。これに対して図1下側の普通のレンズ・カメラでは、一点から出て拡がった光をレンズを通してもう一度一点に集めますから、ピンホール・カメラのような「ボケ」は生じません。撮影対象が近くても、ちゃんとピントを合わせれば、(レンズの収差などは別にして)一点から出た光はきちんと一点に戻って来るのです。
ピンホール・カメラの特徴として、ピント合わせが不要ということがあります。受光面をどこに持って来ても構わないのです。もちろん、孔に近い位置で光を受けるほどボケは小さくなりますが、像も同様に小さくなりますから、撮影後に同じ大きさまで引き伸ばしてしまえば、結局ボケの大きさも同じになってしまいます。つまり、どこでもピントが合う、と言うか、どこでも同じだけボケるのです。
それでは、できるだけ鮮明な画像をピンホールカメラで撮るにはどうすればよいでしょうか。ピンホールが小さくなれば受光面での光の拡がりも小さくなるのですから、孔径を小さくすればするほど鮮明な写真が撮れる・・・・・ならば話は簡単です。ところが光には図2のような「回折」という厄介な現象があって(もちろん「回折」現象が役に立つ場合もありますので、念のため)、そう簡単には行きません。
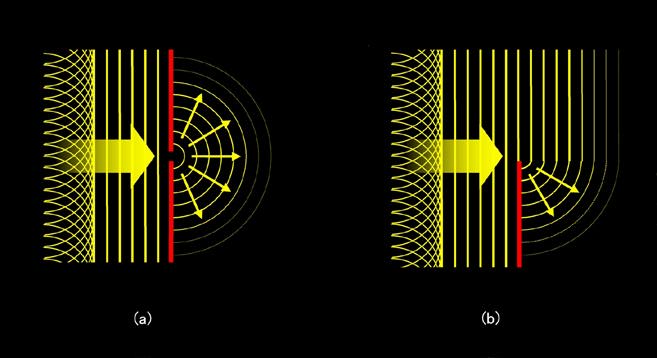
図2 光が陰の部分に回り込む
図2は左から光の波が進んで来る様子を示したもので、波の山の部分(波面)を黄線で表しています。このような見た目は直線的な波の場合でも、波の個々の場所は、そこを中心にして球面状に(図では2次元なので円形に)拡がろうとする性質を持っています。図の左端の部分に示しているように、これらの無数の球面波を重ね合わせた結果、余分な成分が打ち消されて、進行方向に垂直に伸びる山や谷だけが残った、と考えられるのです。実際に図2(a)や(b)のように障害物を置くと、それまでは完全に打ち消されて隠れていた球面波が姿を現し、陰の部分に回り込むように拡がって行く様子が見られます。ピンホールカメラの場合も図2(a)と同じで、本来は陰になるはずの部分にも光が滲み出すことになりますから、ボケの径はピンホール径よりも大きくなるのです。とは言うものの、どのみち同じように光の滲み出しが起こるのであれば、やはりピンホール径を小さくした方が、最終的なボケは小さくできるように思えますね。ところが、ここに「干渉」の要素が入って来るために、必ずしもピンホール径が小さい方が有利とは言えなくなるのです。その様子を図3に模式的に示しました。
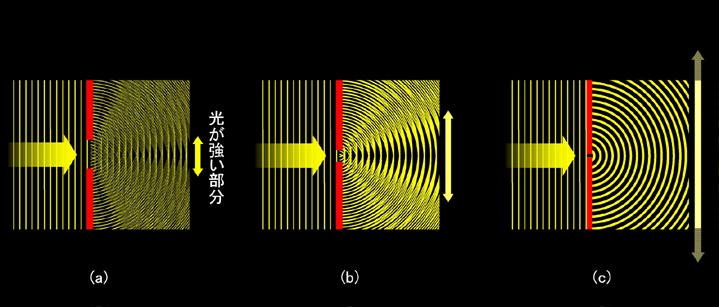
図3 「干渉」で光に強弱のパターンが発生
左から平行光線がやって来て、ピンホールを通り抜けます。この時、現実のピンホールには一定の大きさがありますから、図2(a)のように1個だけ球面波が出るわけではなく、エッジの部分や中央部、反対側のエッジの部分など、とにかくピンホールの中のいたる所から無数に球面波が発生しているはずです。これら無限個の球面波を重ね合わせる、つまり干渉させることで、光がどのように抜けてくるかを調べることができるのです。とは言っても、実際に無限個の波を重ねてみることはできませんので(もちろん積分を使えば計算できますが、図にするのはたいへんですので)、ここでは適当に間引いて表示してみました。その分あまり厳密ではありませんが、これでも干渉による独特の縞模様はちゃんと見ることができます。
黄線は波の山の部分ですから、これが密集した部分は強め合って高い山になっていることを意味します。また黒く抜けた部分は波の谷どうしが重なっていますから、やはり強め合って深い谷になっています。一方その中間の黄線がまばらな部分は、山と谷が重なっているので、逆に弱め合っている場所です。このように光の強いところ、弱いところが縞模様のようになって現れ、そのパターンが左から右へと流れて行くことになります。実はこれが、図2(a)に大雑把に示した光の滲み出しの本当の姿なのです。
まず図3(a)の、ピンホール径が大きい場合を見てみましょう。ちょっとわかりにくいかもしれませんが、ピンホールをまっすぐに通り抜けた中央付近に、ピンホール径と同じぐらいの幅で、黄色と黒のコントラストがはっきりした部分がありますね。黄黒のコントラストがはっきりしているということは、干渉で強め合った高い山(黄線が密集した部分)と深い谷(黒く抜けた部分)が次々に押し寄せて来ることを意味しますから、この部分は光が強いということになります。その外側の領域にも光は回り込んでいますが、その強度は中央部分と比べると小さいので、結局、ピンホールを抜けて来た光の大部分は中央付近に集中すると言えます。しかしよく見ると、この光が強い領域は右に行くほど拡がっていることがわかります。つまりピンホールを通り抜けた光の束は、干渉の効果によって徐々に拡がって行く性質があるのです。
次に、ピンホール径が小さい場合です(図3(b))。今度は中央付近の黄黒のコントラストがはっきりした部分が、明らかに大きく扇型に拡がっています。このようにピンホール径が小さくなると、光の干渉の効果で、光の強い部分がピンホール径よりもはるかに大きく拡がってしまうのです。ついでに言うと、扇型に拡がった光の外側には、干渉で光が打ち消された暗い領域と、光が残る領域とが交互に現れます。図ではこれはピンホールから放射状に伸びる縞模様として現れていますが、これを右方向から眺めれば、中央の明るい円を取り囲む同心状の環として見えることになります(同様の環は図3(a)にもあります)。ただしこの環は中央部と比べれば暗いので、ピンホール・カメラの像のボケにはあまり関係ありません。問題になるのはあくまでも中央部の光の拡がりです。
ピンホール径を小さくするほど光が拡がるという現象は、もっと極端な例を考えてみればいっそうわかりやすくなります。例えば図3(c)のように、ピンホール径が無限小(図では示せないので有限の大きさに描いていますが)で、球面波が1個しか通れないような場合は、180°すべての方向で光の強さは同じになります。つまり、ピンホールを抜けて来た光は無限に大きく拡がってしまうのです。また図には示していませんが、逆にピンホールが非常に大きい極限では、もはやピンホールがないのと同じですから、平行光線がそのまま通り抜けてしまいます。この場合は光は全く拡がらないのです。
このように見て来ると、ピンホール径を小さくすることは、解像度を上げるためには却ってマイナスである、という気がして来ますね。ただし、ここで注意が必要なのは、図3の例は非常に極端なケースだということです。図3では干渉の様子を見やすくするために、ピンホールの径を実際にはあり得ないほど小さく描いています。可視光線の波長は500nm前後ですから、この縮尺で行くと、一番大きい図3(a)でもピンホール径は2μmほどしかありません。現実のピンホール・カメラの孔径はずっと大きくて、0.1mm〜0.5mmぐらでしょうから、光の拡がりは図3よりもはるかに小さいことになります。光の拡がりがピンホール径と比べて無視できるほど小さければ、単純にピンホール径を小さくした方が光を細く絞れることは言うまでもありません。
それでは、実際のピンホール・カメラの場合、ピンホールの径をどれくらいにしたら光を最も細く絞ることができるか、ということを考えてみましょう。先に書いたように、ピンホール径が大きい時には、干渉による光の拡がりは無視できます。しかしピンホール径が小さくなって来ると、干渉による光の拡がりが次第に大きくなり、ついにはピンホール径を越えてしまいます。こうなると、それ以上ピンホール径を小さくしても光の拡がりは大きくなる一方で、全く効果はありません。この様子をグラフで示したのが図4です。
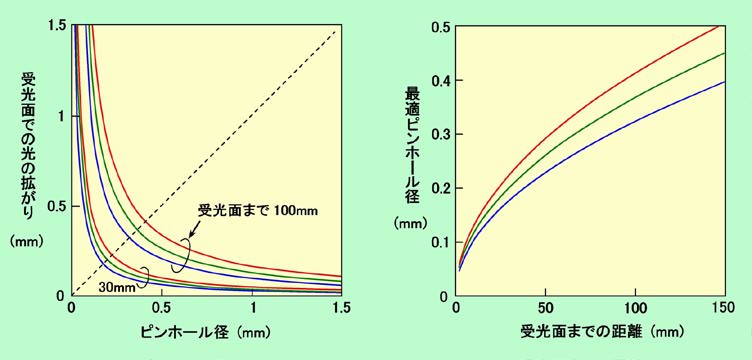
図4 最適なピンホール径を見つける
図4(a)は、ピンホール径を変えた時に光の拡がりがどのくらいになるかを示したグラフです。ピンホールから受光部までの距離(レンズ・カメラに倣って、これを「焦点距離」と呼ぶこともあります。「焦点」のないピンホール・カメラに「焦点距離」と言うのも変な話ではありますが・・・・・)が遠くなると当然光の拡がり幅も大きくなりますから、ここでは距離が100mmの場合と30mmの場合を載せています。また、それぞれ赤、緑、青の3本の線を引いていますが、これは光の波長(つまり色)によって効果が違うからで、それぞれ700nm(赤)、550nm(緑)、430nm(青)の光に対応しています。同じピンホール径であっても、波長の長い赤い光の立場で見れば、青い光から見た場合と比べて相対的に径が小さいことになり、光の拡がりは大きくなるのです。
この図からわかるように、ピンホール径が小さくなると、光の拡がりは急激に大きくなります。左下から右上に向かう45°の破線はピンホール径そのものを表していますが、この破線との交点が、ちょうど干渉による光の拡がりとピンホール径とが同じになるポイントです。つまり、これよりピンホール径を小さくしてもムダ、ということで、このポイントが、光を最も細く絞れる最適なピンホール径を示しているのです。
図4(b)は、このようにして求めた最適ピンホール径を、受光部までの距離に対してプロットしたものです(色違いの3本の線は、(a)と同じく赤、緑、青の光に対しての最適値です)。例えばピンホールと受光部が10cm離れたカメラの場合、緑の光に対する最適なピンホール径は0.37mmということになります。ピンホール・カメラを手作りする時には、このグラフが参考になると思います。
レンズでも回折は起こる
先に、レンズ・カメラはピンホール・カメラと違って光が一点に集まるからボケは生じない、と書きました。しかしこれは回折・干渉の影響を考えない場合の話であって、厳密にはレンズの場合でも光の回折・干渉を考慮しなければなりません。
図5は、平行光線がレンズによって一点に集められる様子を示したものです。空気中と比べてガラスなどの中では光の速度が落ちます。凸レンズは中心部が分厚く、周辺に向かうほど薄くなりますから、周辺の光の方が早くレンズを抜け出て先を進むことになります。その結果、初めはまっすぐだった波面が、レンズを抜けると図のように曲がり、焦点に集まることになるのです。
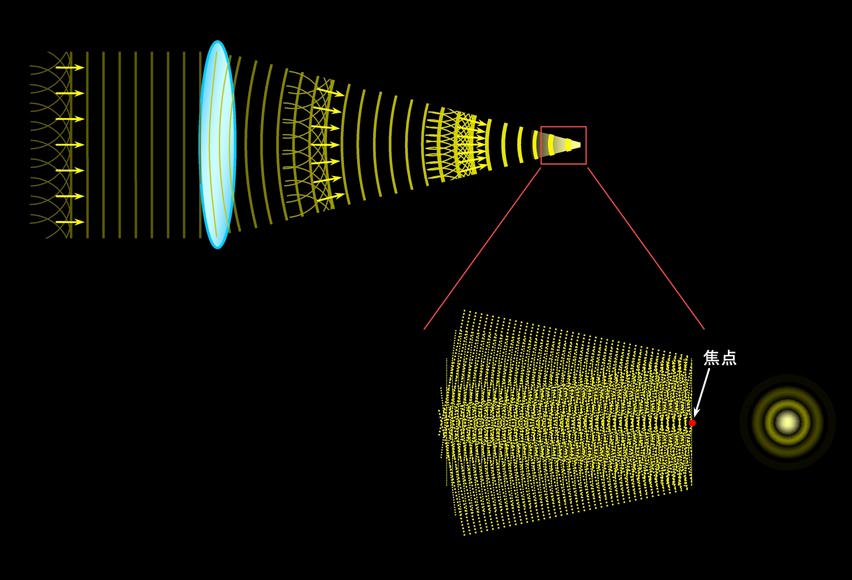
図5 レンズの場合の回折・干渉
この場合も図2や図3と同じように、光の波の個々の場所では球面波が発生している、と考えることができます。レンズを通り抜けると、その球面波が焦点に向かって進行方向を変えます。そして焦点の部分では、レンズのいたるところからやって来た球面波が重なり合うことになるのです。図5の下側には、違う方向から集まって来た5つの波が重なる様子を示しています。この図を見ると、黄黒のコントラストがはっきりした部分、つまり光が強い部分が中央を左右に走り、その上下にも幾重かに光の強い部分があることがわかると思います。これを右の方から見ると、図の右側に描いているように、中央に明るい円、その周囲に同心円状にいくつかの光の環が見えることになります。この様子は図3のピンホールの場合とよく似ていますね。実は起こっている現象は、ピンホールでもレンズでも同じなのです。ただ、ピンホールの場合は孔を抜けた光がそのまま進むのに対して、レンズではそれが一点に集まる、という点が違っているだけで、回折・干渉によって発生した光の滲み出しは、ピンホールでもレンズでも、直径が同じならば同じになるのです(図6)。
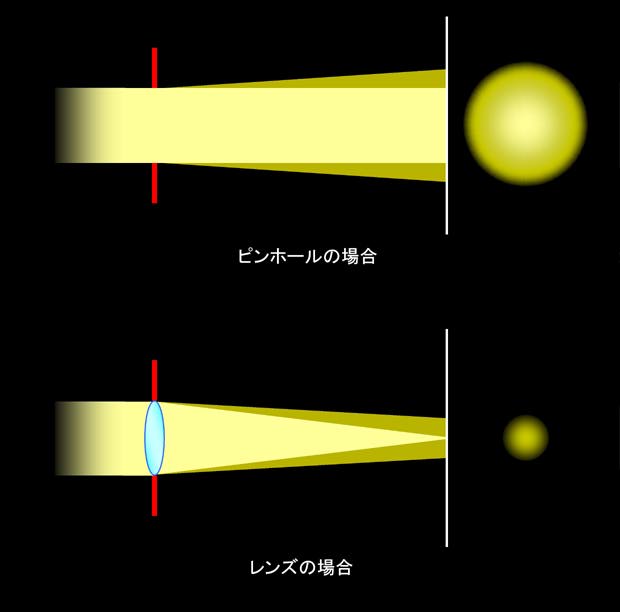
図6 ピンホールでもレンズでも、径が同じなら光の滲み出しは同じ
ところで、「ピンホールとレンズの径が同じ」ということは現実的にはまずありません。ピンホールは1mm以下ですし、レンズは小さくても数mm、大きい物では10cm以上もあります。そして図3で示したように、径が大きくなるほど光の滲み出しは少なくなるのですから、現実のレンズ・カメラの光の滲み出しは、ピンホール・カメラと比べてずっと小さい、ということになります。例えば直径3cm、焦点距離10cmのレンズの場合、滲みの部分の半径は0.003mm(3μm)もないのです。この程度なら無視してもよい、と言いたいところですが、実際にはそうは行きません。ピンホール・カメラでは元々のピンホールの径から来るボケが大きいので、それに比べて光の滲み出しが十分に小さければ無視してもよかったのですが、レンズ・カメラの場合には光は本来一点に集まる、つまりボケがない状態が基本になるのですから、滲み出しはそのままボケの大きさになってしまいます。本来の解像度が高いために、小さくてもアラが目立ってしまう、ということです。もちろん、レンズの直径が大きくなればなるほど、また焦点距離が短くなればなるほどボケは小さくなる、という点は、ピンホールの場合と変わりありません。つまり直径と焦点距離が、カメラの解像度に大きく影響するのです。この点については、次の節でもう一度詳しく説明します。
レンズ・カメラの性能
前の節で、レンズで起こる光の滲み出しについて説明しましたが、それも含めて、レンズ・カメラの性能、特にレンズの性能にかかわる話をまとめておきましょう。レンズによって像ができる基礎的な仕組みについては
光学機器の話で取り上げていますので省略して、ここではレンズの特徴を表す2つの数値、口径(単純な直径ではなくて、固定枠や絞りで制限された、実際に光が通る部分の直径)と焦点距離に注目して、カメラの性能、と言うか、特徴を考えてみます。
「望遠」と「広角」 ― 違うのは像の大きさだけじゃない ―
焦点距離が長いのは「望遠レンズ」で、短いのは「広角レンズ」、と言う話は
光学機器の話にも書いていますが、ここでも改めてそれを確認しておきましょう。図7(a),(b)は焦点距離の違うレンズで景色を写したときの様子を示しています(本当ならば景色はもっと遠くに置きたいところですが、光路図を描く都合上、かなりレンズに近いところに配置しました)。当然ながら、焦点距離の長い(a)の方が像は大きくなります。
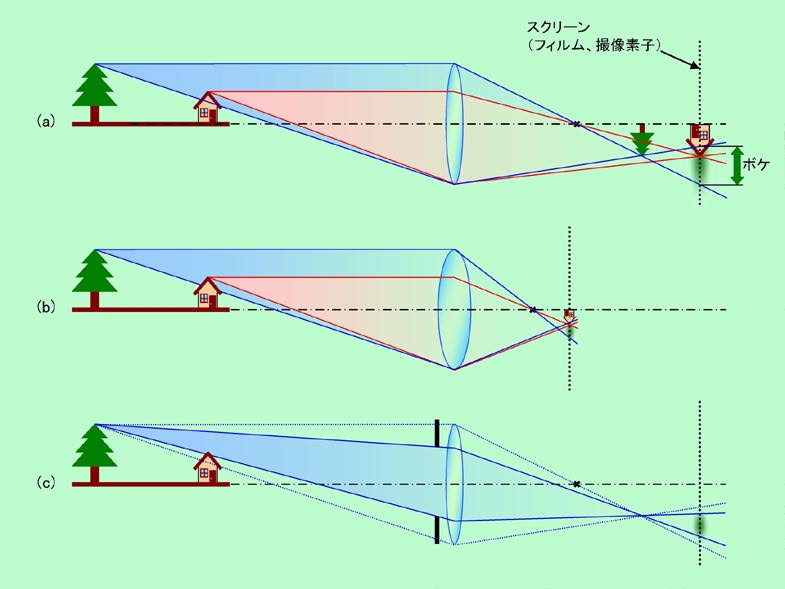
図7 焦点距離の違うレンズで像を作る
像が大きいということはそれだけ景色が拡大されて写るということですから、これは「望遠」、一方、像が小さい(b)の方はそれだけ広い範囲が写せますから「広角」です。通常は、肉眼で見た時に近い感じの写真が撮れる焦点距離(普通の35mmフィルムカメラの場合は50mm)のレンズを「標準レンズ」、それよりも焦点距離が長いレンズを「望遠レンズ」、焦点距離が短いレンズを「広角レンズ」と呼んでいます(
光学機器の話参照)。ただし、デジタルカメラの場合は撮像素子がフィルムよりも小さく、同じ焦点距離のレンズでは写せる範囲が狭くなってしまいますので、標準レンズに相当する焦点距離はもっと短くなります。フィルムカメラよりもちょっとだけ撮像素子が小さい一眼レフの場合は35mm前後、コンパクトカメラでは10mm以下になる場合もあります。実際にコンパクトタイプのデジタルカメラには、10mm程度の非常に焦点距離の短いレンズが付けられているのが普通で、これでちょうど標準的な大きさの写真が撮れるのです。
ところで、望遠レンズと広角レンズの違いは、像の大きさだけではありません。図7をもう一度見てください。ここでは手前の家の像がスクリーン上にできるように、つまり家にピントを合わせていますが、その時、奥の木はどう写っているでしょうか。木にピントが合うのはもっとレンズ寄りのところ(青い線の交点)ですから、スクリーンの位置では一点に集まっていた光が再び拡がってピンボケ状態になっています。そのボケ具合を2つのレンズで比較してみると、焦点距離が長い(a)の方が明らかに大きいのです。これは何を意味するかと言うと、焦点距離の長い望遠レンズを使うと、狙った物より遠くにある物や近くにある物が著しくボケる、ということなのです。逆に焦点距離の短い広角レンズを使えば、手前から奥まで比較的ピントの合った写真が撮れることになります。もちろん広角レンズの場合でも、本当にピントがピタリと合うのは特定の距離にある物だけですが、ボケが人間の目で識別できないくらい小さければ、事実上はピントが合っていると見なしても問題ありません。この「事実上ピントが合っていると見なせる範囲」のことを「被写界深度」と呼びます。望遠レンズは被写界深度が浅く、広角レンズは被写界深度が深いのです。
この被写界深度は、レンズの焦点距離だけではなく、絞りによっても変えることができます。図7(a)のように絞り開放の状態で撮影すると、レンズを通る光の束が太くなりますから、焦点を外れたときのボケ幅も大きくなり、被写界深度は浅くなります。反対に、図7(c)のようにグッと絞った状態にすると、ボケ幅が小さく抑えられて、被写界深度は深くなるのです。
写真のテクニックとして、被写界深度のことは知っておいて損はありません。例えば、ポートレートで人物だけを強調して写したい時や、野原の中の特定の一輪だけを目立たせたい時などは、絞りを開き気味にして、少し離れたところから望遠で狙うと、前景や背景がうまくボケてくれます。逆に旅行の記念写真などで、手前の人物と遠くの景色の両方を鮮明に写したい場合は、広角レンズを使って、少し絞って撮影した方がよいのです。ただし、このテクニックを駆使しようとしても、コンパクトタイプのデジカメではなかなかうまく行きません。元々焦点距離が非常に短いレンズが付いている上、レンズの径も小さいので、被写界深度をあまり浅くできないのです。これは、遠くも近くも鮮明に写せるという利点でもあるのですが、技巧を駆使するには不便、というわけです。
像の大きさ(あるいは写る範囲)と被写界深度の他にも、焦点距離によって変わるものがあります。「パースペクティブ」と呼ばれる、いわゆる「遠近感」で、これが変わると見え方がガラッと変わります。例えば図8のダンボール箱を並べたような物体を焦点距離の違うレンズで撮影した場合を考えましょう。薄い黄色で示したのが実際に撮影される範囲で、焦点距離の長い(a)の方は角度が狭く、焦点距離の短い(b)は広い角度をカバーしています。物体を同じ距離に置くと当然(a)の方が大きく写りますから、レンズからの距離を変えて、ほぼ同じ大きさ(画面全体の8割程度)に写るようにしてあります。
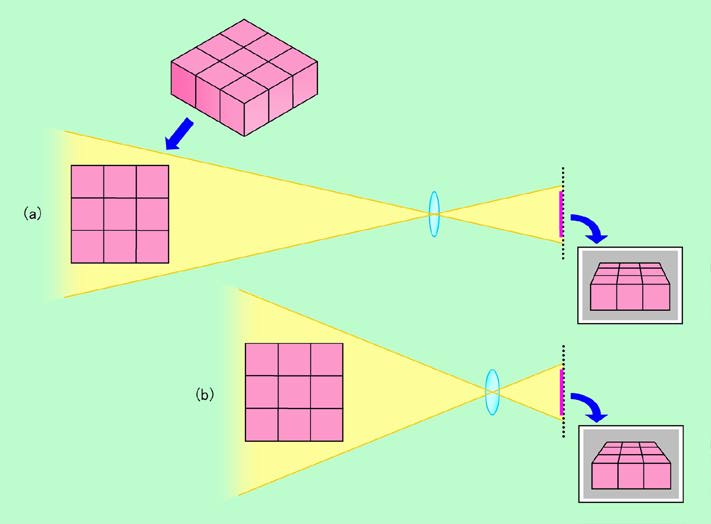
図8 遠近感は焦点距離しだい
実際にどのように写るかを、図の右側に示しました。エラく雰囲気が違いますよね。(b)の広角レンズの場合には、遠くに行くほど極端に広い範囲が写り込みますから、相対的に箱の向こう側の辺は短く写ります。その結果、非常に奥行きのある画像に仕上がるのです。これに対して(a)の望遠レンズでは、向こう側の辺はあまり短くなりません。もっと焦点距離を長くすると、本当に奥行きのない、ノッペリした画像になってしまいます。
このような特徴を利用すると、本当はたいして広くもない部屋を、実際以上に広く見せることもできます。広角レンズで、目いっぱい対象に近付いて撮ればいいのです。またマラソン中継などで、本当はずっと離れているはずの後続の選手がすぐ近くまで迫っているように見えることがよくあります。これは、選手の前方のかなり離れた中継車から望遠レンズで撮影しているからで、奥行きがグッと圧縮されて見えてしまうのです。
レンズの明るさ ― どれだけ明るい像を作れるか ―
明るさと言っても、レンズは電灯のように自分で光を出すわけではありませんので、これは「どれだけ明るい像を作れるか」ということを意味します。すぐにわかると思いますが、レンズの口径が大きいほど多くの光を集められますから、像は明るくなります。口径が2倍になれば面積は4倍ですから、4倍明るくなるのです(図9(b))。また、作られた像が小さいほど、明るさは増します。同じ量の光を狭い範囲に集めるのですから当然ですね。そして像の大きさは、先に書いたように焦点距離で決まりますから、焦点距離が短いほど明るくなる、ということになります。無限遠方の物体の場合は、図9(c)のように、焦点距離が半分になると像の大きさも半分になりますので、面積は4分の1。つまり明るさはやはり4倍になります。
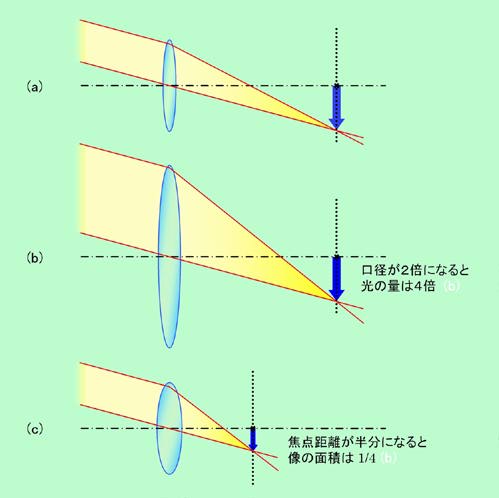
図9 像の明るさは口径と焦点距離で決まる
口径が大きいほど、また焦点距離が長いほど像が明るくなる、ということから、これら2つの要素をひっくるめて、焦点距離を口径で割った値を考えれば都合がよくなります。これがいわゆる「F数」です。F数が小さいほど明るいレンズであることを意味し、例えばF=1.4のレンズは、F=2のレンズと比べて2倍明るい像を作ることができるのです。また、同じレンズでも絞りを効かせれば口径が小さくなりますから、F数はどんどん大きくなります。カメラレンズの絞り環に目盛ってある数値は、絞り孔の直径ではなくて、このF数なのです。
F数が小さいほど明るい像ができるのですから、それだけ暗い対象の撮影ができるようになります。またシャッタースピードを速くできるので、高速で動く物体を捉えやすくなりますし、手ブレの防止にも有効です。もちろん、先の被写界深度の調整やレンズの収差を減らすために、わざと絞りを効かせてF数を大きくすることはよくあります。しかし、どんなにがんばっても元の状態よりも明るくすることはできないわけですから、やはり元のF数が小さいレンズの方が、いろいろ細工をする余裕が十分にあって有利だと言えます。ちなみに、ピンホール・カメラの場合もF数を考えることができます。孔径が1mm以下で、受光面までの距離は5cmとか10cmですから、F数は非常に大きくて100とか300。その結果、シャッタースピードは普通のカメラの何千倍も遅くなって、数十秒も開けっ放し、ということになるわけです。
解像度 ― どれだけ細かいところまで写るか ―
どれだけ鮮明な画像が撮れるか、どれだけ引き伸ばしに耐える写真になるかは、レンズの持っている解像度に依る部分が多くなります。単純に、「高性能のレンズほど像は鮮明になる」のでしょうか? そもそも「高性能」とは何でしょうか?
普通に「高性能」と言えば、「収差が少ない」ということでしょう。ここで「収差」に関する細かい話はしませんが、とにかくレンズには必ず「収差」があって、ボケや歪のない完璧な像を作ることができる理想的なレンズは存在しません。そこで実際のカメラのレンズは、性質の違う多数のレンズを複雑に組み合わせて、収差をできるだけ減らすように設計されています。このような「収差の補正」がキチンとされて、理想に近い状態になっているレンズが「高性能のレンズ」ということになります。もちろん、「いいレンズ」はそれだけ値段が高くなりますが・・・・・。
それでは「収差のない」理想的なレンズならば、解像度は無限に高くなるのでしょうか? 実は、そうは行きません。先に、レンズの場合でもピンホールと同じように回折・干渉による光の滲み出しが起こる、ということを説明しましたが、これが解像度の限界を決めてしまうのです。
もう一度、図5を見てください。ここでは収差のない理想的なレンズを想定していますが、焦点に集まった光は完全な「点」になるのではなく、同心状の環に囲まれたボケた円になっています。周りの環は暗いので無視するとして、真ん中の円の直径が、そのレンズの解像度の限界、ということになります。「解像度」という言葉にはやや曖昧なところがあるので、「分解能」という言い方に変えた方がわかりやすいかもしれません。これは図10に示すように、接近した2点を見分ける能力のことです。
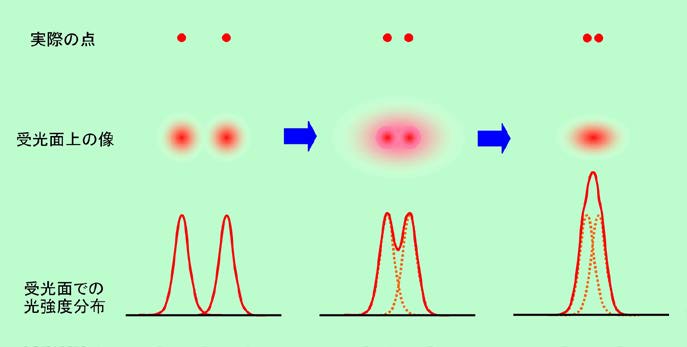
図10 分解能とは接近した2点を見分ける能力
対象物上の実際の点は、前記のようにレンズを通して像にするといくらか拡がったボケた円になります。光の強度分布で見ると、中央が強く、周辺に行くほど弱くなる山型で表されます。図の左端のように2つの点が離れている時には、像の方でも2つの点として容易に区別ができますが、これが接近して来ると、やがては山裾が重なり合うようになります。そしてついには一つの山のようになって、全く区別ができなくなってしまうのです。当然、ボケが小さいほど山裾の重なりは少ないですから、2点を識別する能力は高くなります。
図5、図6のところでもちょっと触れたように、ボケの原因となる光の滲み出しは先へ進めば進むほど大きく拡がって来ますから、レンズの焦点距離が長いほど、ボケは大きくなります。またピンホールの場合と同じように、口径が大きくなるほど光は中心に集中して、ボケは小さくなります。ということは・・・・・もうおわかりと思いますが、F数が小さいレンズほど、回折・干渉によるボケは小さくなる、つまり分解能は高くなるのです。焦点距離の方は、どんな写真を撮りたいかでおよそ決まってしまいますから、口径が大きなレンズほど分解能を高くできる、と言ってもよいでしょう。具体的な数字を挙げると、F=1.4のレンズでは、受光面でのボケの直径は1.88μmぐらい、F=8のレンズでは10.7μmぐらいになります(光の波長550nmで計算)。受光面上でこの距離の半分ぐらい離れた点ならば何とか2つの点として区別できるとすると(図10の中央の状態)、F=1.4では0.94μm、F=8では5.4μmが限界、ということになりますね。これを受光面上の距離ではなく、2点を見込む角度で表すと、今度はレンズの焦点距離は関係なくなって、口径だけで決まります(焦点距離が長くなるほどボケの直径は大きくなりますが、その時の広がり角度は一定ですから)。口径4mmのレンズでは分解角度の限界は35"(35秒:1秒は1度の3600分の1)、口径35mmのレンズでは4"ぐらいです。人間の目の分解角度が約60"(視力1.0の場合)ですから、口径35mmだと、その十数倍の能力と言えますね。
なお、カメラだけでなく
望遠鏡や
顕微鏡などの分解能に関しても、全く同じことが言えます。これらの光学機器では、対物レンズで作った像を接眼レンズでさらに拡大するわけですが、接眼レンズの側でどんなに倍率を高めても、対物レンズでちゃんと解像できていなければ全く意味はありません。カメラで撮った写真を虫眼鏡で拡大して見ているようなものですから、元の像を作る対物レンズの重要性は、むしろカメラよりも大きいと言えるでしょう。
ところで、レンズの分解能がいくら高くても、フィルムや撮像素子の能力がそれに追いついていなければ、写真としては意味がありません。また、プリンターで印刷することを考えると、プリンターの方の解像度も気になります。これらの関係はいろいろ複雑ですが、この際、細かい話は抜きにして、現状の代表的なコンパクト・デジカメと一眼レフタイプのデジカメについて、数字を比較してみましょう。F数は2.8に統一し、参考として普通の35mmフィルムを使う一眼レフの数字も挙げておきました。
表 解像度の比較
|
コンパクト・デジカメ |
一眼レフタイプ・デジカメ |
35mmフィルム一眼レフ |
| レンズ口径 (mm) |
3 |
12 |
18 |
| 焦点距離 (mm) |
8.6 |
33 |
50 |
| F数 |
2.8 |
2.8 |
2.8 |
| 受光部のサイズ (mm) |
6.2×4.6 |
23.7×15.6 |
36×24 |
| 受光部での最小分解距離 (μm) |
1.88 |
1.88 |
1.88 |
| 最小分解角度 (秒) |
45 |
12 |
8 |
| 光学的限界で決まる最大画素数 |
約800万(8メガピクセル) |
約1億(100メガピクセル) |
約2.5億(250メガピクセル) |
| プリンターの画素数(L版) |
150万 |
| プリンターの画素数(A4) |
870万 |
コンパクト・デジカメは、小型・軽量にするために、レンズも撮像素子も非常に小さなものを使います。これで普通のフィルム・カメラと同じ範囲が写るようにしなければなりませんから、レンズの焦点距離もかなり短くなっています。これに対して一眼レフタイプのデジカメは、35mmフィルムを使う一眼レフに近いサイズのレンズや撮像素子を使っています。撮像素子がフィルムよりも少し小さいので、レンズの焦点距離や口径がやや小さくなっていますが、それでもコンパクト・デジカメと比べれば、レンズや撮像素子の面積は10倍以上もあるのです(実際にはもっといろいろなサイズのカメラが出回っていて、一回り大きいコンパクト・デジカメやフィルムカメラと同じ仕様の一眼レフ・デジカメもあります)。
F数を揃えているので、受光面での最小分解距離は同じです。一個一個の画素をこれより小さくしても意味はありませんから、この大きさが最小の画素サイズになります。しかし撮像素子の大きさが違うので、カメラによって全体の画素数には大きな開きが出て来ます。ここに例を挙げたコンパクト・デジカメでは800万画素が限界であるのに対して、一眼レフタイプでは1億画素、つまり100メガピクセルまで、数字の上では画素数を増やせるのです。現在出回っているデジカメの画素数は、コンパクト・デジカメで数百万、一眼レフで1千万〜2千万というところですから、コンパクト・デジカメでは既に限界に近く、一眼レフではまだ余裕がある、ということがわかります。ちなみに、高精細のフィルムの解像度は2000万画素相当と言われています。フィルムの場合は粒子の形や大きさが揃っていませんし、そもそも色分解などの露光の仕組みが違うので単純比較はできないのですが、最近のデジカメは少なくとも数字上ではフィルムカメラと同レベルのところまで来ていると言えます。
それではプリンターの方はどうでしょうか。インクジェットプリンターの解像度を表すのに"dpi"という単位がよく使われます。これは1インチに何ドット打てるか、ということを表す数値ですが、1ドットがそのまま1画素になるわけではありません。
色の話にも書いているように、印刷の濃さ(階調)はドットの密度で表しますから、ある程度のドットがまとまって一つの画素を作ることになります。というわけで、例えば数千dpiのインクジェットプリンターでも、実質的には1インチ当たり300個程度の画素しか表示できないのが普通です。また、昇華型プリンターのように、1個のドットで階調表現ができるプリンターの場合でも、1インチ当たりの画素数はやはり300程度です(実は、これ以上解像度を上げても、人間の目ではわからないのです)。そこで、この300画素/インチを基準にしてプリンターの画素数を計算すると、上の表のように、L版(12.7cm×8.9cm)に印刷した時の総画素数は約150万、A4(29.7cm×21.0cm)に印刷した時の総画素数は約870万となります。これがプリンターの性能をフルに引き出すために必要な画素数、ということになるのです。
L版への印刷ならば、初期のデジカメを除けばカメラ側の画素数が問題になることはまずありません。200万〜300万画素あれば余裕です。しかしA4まで引き伸ばすとなると、コンパクト・デジカメでは少々苦しくなって来ます。実質的に600万〜800万画素あれば十分と言われていますが、細かいところを気にすれば800万画素以上が欲しくなるでしょう。そうなると、上の表に示したようにレンズや撮像素子の大きさから決まる限界が見えて来るのです。
光学的な限界がある以上、コンパクト・デジカメの画素数を大幅に増やそうとすれば、撮像素子を大きくし、それに合わせてレンズも大きくするほかはありません。これに対して一眼レフの方は、光学的にはまだ余裕がありました。それならばコンパクトカメラ並に画素の小さい撮像素子を使って、もっと画素数を増やしてもよさそうなものです。
本当に「画素数」=「画質」ならば、それもアリでしょう。しかし実際には、画素数が多いから高画質、とは言えません。画素が小さくなると一画素当たりの光の量が減ってしまいますから、光の強度を測定する精度が下がり、元の情報を忠実に再現する能力が低下してしまうのです。このような事情がある上に、画素が増えるとデータ量が膨大になることや、先ほどのプリンターとの兼ね合いなどもあり、現状では2000万〜4000万画素ぐらいが上限になっています。もちろん、美術品の高精細撮影などの特殊な用途に関しては、いろいろと工夫を施して1億を越えるような画素数の撮影機も作られています。
シャッターのイタズラ
レンズの性能を中心にいろいろと書いて来ましたが、最後に、それ以外のトピックスを2つ。まずはシャッターに関する話題です。
一般的なフィルム・カメラでは、レンズの部分に取り付けるレンズ・シャッターと、フィルムの直前に取り付けるフォーカルプレーン・シャッター(フォーカルプレーン=焦点面)の2種類があります。レンズ。シャッターは絞りにそのままシャッター機能を持たせたような感じで(実際に絞りを兼ねているものもあります)、小型・軽量にできるのでコンパクトカメラによく使われています。一方フォーカルプレーン・シャッターは、フィルム面に蓋をする形になりますからレンズ交換が容易で、速いシャッタースピードも出しやすい、ということで、もっぱら一眼レフに使われています。このフォーカルプレーン・シャッターが、ちょっとしたイタズラをすることがあるのです。
フォーカルプレーン・シャッターは、基本的には図11のように、先膜(図では黒色で表示)、後膜(灰色で表示)と呼ばれる2枚の膜で構成されています。それぞれの膜には露光用の窓が開いており、これが受光部の前を高速で横切るのです。
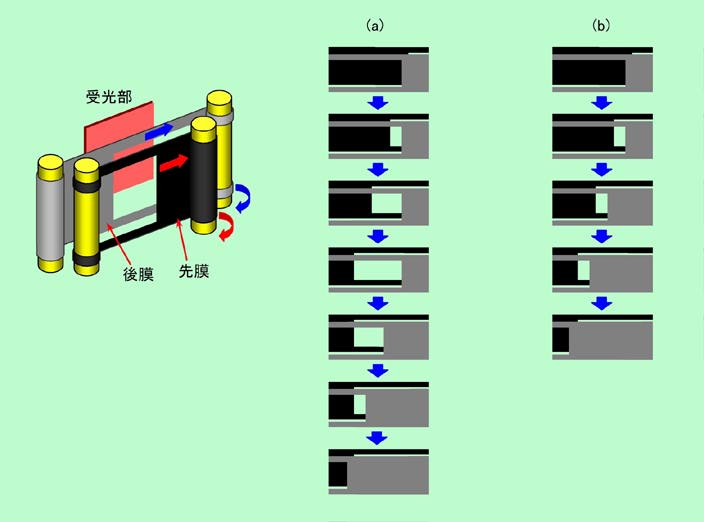
図11 フォーカルプレーン・シャッターの仕組み
低速シャッターの場合は図11(a)のように、まず先膜が全開状態まで動き、次いで後膜が動いてシャッターが閉じます。後膜がスタートするタイミングを遅らせれば、いくらでもシャッタースピードを遅くすることができます。一方、高速シャッターの場合には、図11(b)のように、先膜が全開になる前に後膜がスタートします。スリット状の開口部が受光部の前を横切る形になるわけで、後膜のスタートを早くしてスリットを狭めれば、実際の膜の速度は一定でも、簡単にシャッタースピードを上げることができます。初期のフォーカルプレーン・シャッターは布膜を使った図11のような横走り方式であったのに対して、最近は金属膜を使った縦走り方式が主流になっていますが、基本的な仕組みは同じです。
一見、完璧に見えるフォーカルプレーン・シャッターですが、ひとつだけ大きな欠点があります。それは、受光部の全面を同時に露光するのではなく、場所によって露光のタイミングがズレるので、動く物を撮影すると歪む場合がある、ということです。その様子を示したのが図12です。ここでは横走りタイプを例に説明しています。
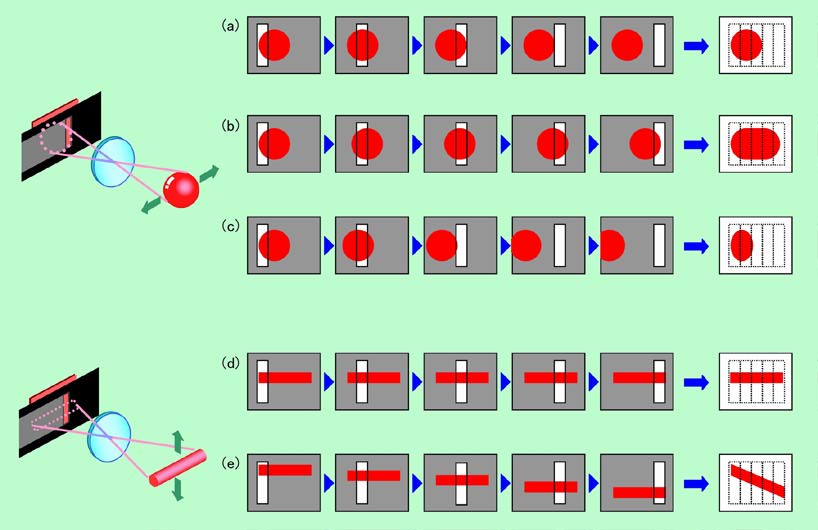
図12 フォーカルプレーン・シャッターによる像の変形
まず、左上の図のように、横方向に動く物体を撮影する場合を考えましょう。物体が止まっていれば、(a)のようにスリットが横に動いて端から順に露光して行っても、何の問題も起こりません。ところが物体が動いて、像がスリットから逃げるように移動する(b)のケースではどうでしょうか。例えば左から4番目の状態を見ると、物体が止まっている(a)の場合にはスリットは既に像から外れています。しかし(b)では4番目どころか5番目の状態でも、物体の像はスリットの中に残っているのです。その結果、最終的に得られる写真は、右端に示すように横に伸びた形になってしまいます。反対に、スリットと逆向きに像が動く(c)のケースでは、像が早めにスリットから外れてしまいますから、左右に押し縮めたような写真になるのです。同様の変形は、左下のように物体が縦に動く場合にも起こります。静止している(d)のケースと違って、露光の過程で縦位置がズレて来ますので、本来は真横に伸びていた物体が、(e)のように斜めに歪んで写ってしまうことになるのです。
もちろん物体の移動速度が遅ければ、このような歪は気にする必要はありません。それでは、どのくらいの速さなら問題になるのでしょうか。最も極端なのは、スリットと同じ速さで物体の像が移動する場合でしょう。像が常にスリットと一緒に動くのですから、端から端までビヨ〜ンと引き伸ばされた写真になってしまいます(ちなみに、像の移動速度がスリットより速くなると、引き伸ばされていた像が再び短くなりますが、今度は左右が反転してしまいます)。仮に、フォーカルプレーン・シャッターの膜の移動速度(スリットが端から端まで動くのに要する時間)を1/60秒としましょう。標準レンズの場合、写真に写る範囲は10m先で7〜8mぐらいですから、7〜8mを1/60秒で走り抜ける物体を撮影すると像はスリットと一緒に移動して、端から端まで引き伸ばされる状態になります。その速度はマッハ1以上。つまり超音速でスッ飛んで行かない限り、こういう状況にはならない、ということです。もっとも、これは像の引き伸ばしが最大になる場合の話であって、もっと遅い速度でも、ある程度の引き伸ばし(あるいは押し縮め)は起こります。例えば、10m先を時速60kmで走る車の場合、約50cm(受光面では2.5mm)伸びて写ることになりますから、長さ4mの車ならば10%以上も変形するわけです。フォーカルプレーン・シャッターではこのような問題は基本的に避けられないので、膜の速度を上げて影響を小さくすることが必要になります。
これに対してデジカメの場合は、電気的なオン/オフをシャッターとして使いますので、このような問題は起きない、と言いたいところですが、実はCMOSという撮像素子を使ったカメラでは、同じような問題が発生します。CMOSでは画素を構成する個々の受光素子が順番に動作して信号を送り出すようになっているため、場所によって露光のタイミングがズレてしまうのです。これを防ぐために、先のフォーカルプレーン・シャッターのような機械的なシャッターを併用して露光のタイミングを合わせ、さらに処理を高速化してズレを最小限に抑える工夫をしています。
もう一つ付け加えておくと、CMOSと並んでデジカメに多く使われている撮像素子にCCDというものがあります。CCDは全画素で同時に露光して電荷を蓄え、これを一斉に通路に移してから順次送り出す方式なので、CMOSのように露光のタイミングがズレるという問題は起こりません。しかし、画面の中に極端に明るい部分があると、そこから縦に光のスジが走る「スミア」と呼ばれる現象が発生します。強い光が当たり続けると、大量に発生した電荷が縦につながった通路に溢れ出してしまうためで、個別に信号を送り出すCMOSでは起こらない現象です。これを防ぐためには、余分な電荷が発生しないように、露光が終わったらすぐに光を完全遮断してしまう機械式のシャッターが有効です。結局のところ、CMOS方式にしろCCD方式にしろ、高機能のデジカメでは機械式のシャッターを併用しなければならない、というわけです。
面白い写真が撮れるスリットカメラ
陸上競技や競馬などでは、着順を決めるために写真判定をすることがあります。この判定用の写真をテレビや新聞で目にすることがあると思いますが、普通の写真と比べて何か違和感がありませんか? まず背景が全く写っていませんし、選手の姿も微妙に歪んでいる感じです。実はこのような着順判定用の写真は普通のカメラではなく、スリットカメラという特殊なカメラで撮られたものなのです。
スリットカメラの原理を、図13に示します。普通のカメラはフィルム全体で光を受けますが、スリットカメラでは図の一番上に描いているようにフィルムの前に縦に細長いスリット(着順判定用のカメラでは幅20〜30μmぐらい)が付けられており、これを通してゴールライン上の映像だけを記録するようになっています。そして撮影時には、スリットが移動するのではなく、フィルムの方を一定速度で巻き上げて移動させるのです。
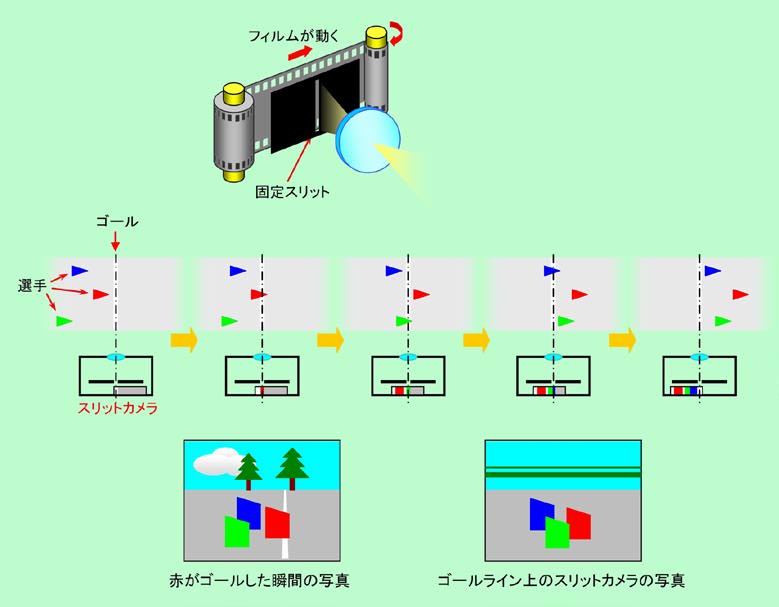
図13 スリットカメラは時間の変化を記録する
図の中段には、あるレースのゴールシーンをスリットカメラで記録した様子を描いています。スリットはゴールラインの延長線上に置かれ、ゴールラインを横切る選手の姿がスリットを通して記録されて行きます。
普通にゴールの瞬間を撮影した場合、確かにその瞬間の順位は正確に記録されます。図の下段左に赤がゴールした瞬間の写真を示していますが、この時点では青が2位、緑が3位です。しかし、この後の順位がどうなるかはわかりません。ここからのわずかな時間に、3位の選手が2位の選手を逆転して先にゴールインするかもしれないのです(図では実際に緑が青を逆転しています)。その点、スリットカメラではこのような問題は起こりません。記録されているのはゴールライン上の映像のみであり、そこを通過する選手の姿が時間と共に記録されているからです(図では緑の方が青よりも先にゴールラインを通過しているので、スリットカメラでは下段右のように緑が先に写っています)。つまりスリットカメラで撮った写真の横軸は、空間的な横方向ではなく、時間を表しているのです。
選手がゴールラインを通過する時、エイトマン(ちょっと古い?)のように同じ姿勢を保っているわけではありません。時間と共に体勢は少しずつ変化しますから、普通の写真と比べるとちょっと妙な姿に写ります。また受光部を動かす速さと実際の速さとの関係で、フォーカルプレーン・シャッターの場合と同じように、横に伸びたり縮んだりすることもあります。これらが、スリットカメラの写真に少し違和感を覚える原因です。さらに背景に関しては、スリットから見える部分だけがズーッと横に流れることになりますので、景色としては写らず、単なる真横の縞模様になってしまいます(図ではゴールラインにかかっている木の枝の部分だけが横に流れて写っています)。
初期のスリットカメラはロールフィルムを巻き上げながら撮影する方式でしたが、最近は当然のようにデジタル化(電子化)が進んでいます。その場合、まさか撮像素子を横に動かすわけには行きませんから(できなくはないでしょうけど)、縦長の撮像素子を使い、スリットから入って来る情報を高速連写で次々にメモリーに送り出すようになっています。ちょうどスキャナーのような感じですね。スキャナーでは素子の方が移動して行きますが、電子式スリットカメラでは撮影対象の方が移動するのです。
ロールフィルム式のスリットカメラは、普通のカメラを改造することで自作することもできます。フィルムの前に0.5mmぐらいの幅のスリットを取り付け、フィルムをモーターで巻上げるようにすればよいのです(こう書くと簡単そうですが、実際にやってみると、細かな調整など、相当に苦労すると思います)。このようなスリットカメラは、列車の撮影などによく使われるようです。フィルムを巻き上げる速度をうまく調節してやると、長い列車をフィルム一本にきれいに収めることもできるのです。
スリットカメラの変形として、パノラマカメラもあります。カメラ本体を回転台の上に乗せ、フィルムを巻き上げると同時に、カメラ自体もくるりと回転させるのです(パノラマカメラにはこの他にもいくつか種類があります)。先の着順判定や列車の撮影では、カメラは固定で対象物が動いたのですが、今度は対象物(景色)が固定で、カメラの方が動くわけです。景色を撮影するスキャナーと言ってもよいでしょう。これで撮った写真は、長いフィルムに継ぎ目なく記録された、まさに本物のパノラマです。
雑科学ホーム
hr-inoueホーム













