
雑科学ホーム
hr-inoueホーム
● 虹の話(その2) ●
虹はけっこう複雑
虹は古くから人々の注意を引いてきました。雨上がりの空にカラフルな巨大なアーチが現れるのですから、注目されない方がおかしいですね。ただ、注目のされ方は地域によって様々なようです。ヨーロッパではどちらかというと縁起の良いもの、という扱いが多く、虹の根元には財宝がある、などという言い伝えもあるそうです(実際には虹の根元には決して到達できない、ということがわかった上での作り話でしょうか)。一方、日本や中国では大蛇や龍に関係づけられ、むしろ不吉なもの、あるいは畏れ多いものとされることが多かったようです。「虹」という字が「虫へん」なのも、蛇や龍を意識してのことでしょう。昔の和歌に虹がほとんど登場しないのも、このあたりの事情によるようです。
もちろん現代の人間は、虹が分光現象であることを知っています。空気中に浮かんだ水滴で太陽の光が屈折、反射され、光の波長、つまり色ごとに分離されたもの。確かにその通りなのですが、球形の水滴でなぜ特定の方向に特定の色の光が出るのか、なぜ2つの虹が見えることがあるのか、なぜアーチ状になるのか、プリズムで人工的に作る虹とはどこが違うのか、あるいは同じなのか・・・等々、よく考えてみるといろいろと疑問が湧いて来ます。本項では、この誰もが知っているけれど、実はけっこう複雑な現象である虹について、虹によく似た他の現象も含めて、少し詳しく見て行くことにします。
なお、本項だけでも独立して読めるようにしていますが、プリズムや回折格子が作る虹と関連する部分も多いので、
虹の話(その1)と併せて読んでいただければ、より理解が深まると思います。
水滴による光の散乱
空の虹が、空気中に浮かぶ水滴によって太陽光線が散乱されてできることはご存知でしょう。基本原理は
プリズムと同じ、ということで、プリズムを例に引いた解説記事はよく目にします。ですが、プリズムで起こっていることと空の虹で起こっていることは全く同じなのでしょうか。確かに、光の波長によって屈折率が違うために色ごとに光の進行方向が変わる、という点はプリズムと同じです。しかし、プリズムは三角形で水滴は球形です。三角形のプリズムならば、プリズムの面のどこに光が入っても角度は一定ですし、出て行く方向も面に対して決まった角度になるでしょう。これに対して球形の水滴の場合は、同じ方向の光でも球のどの位置に光が入るかで表面に対する角度が違いますから、最終的に出て行く方向も一定にはならないはずです。それにもかかわらず、なぜ球形の水滴で特定の角度への光の散乱が起こるのでしょうか。これを理解するには、光が水滴の中をどのように進むのかを詳しく知る必要があります。
水滴中の光の経路を示したのが図1です。この経路は、水滴の屈折率がわかれば正確に計算、あるいは作図で求めることができます。
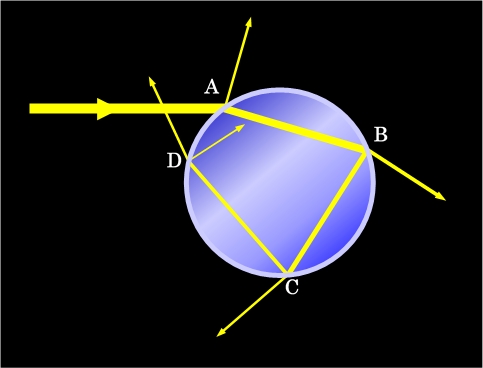
図1 球形の水滴に入った光の経路
左から太陽光線がやって来て、A点で水滴に入射したとします。一部は上方に反射され、一部は水滴の内部に、屈折の法則に従った角度で侵入します。反射光の方は元の太陽光が跳ね返っただけですから、虹とは関係ありません。内部に侵入した光はB点に達し、一部は屈折して外へ出て、一部は反射されて再び水滴中に戻されます。このB点で外に出て行く光は2度屈折していますから色に分かれているはずですが、図の右方からこの光を見ようとしても、強烈な太陽光と重なるので見ることができないでしょう。また、詳しい説明は省略しますが、後述の虹を作る光のように特定の方向に強く出ることもありませんから、この光も虹とは関係ありません。B点で内部に戻された光は、今度はC点でさらに2つに分かれます。ここから外に出て来る光は、太陽に背を向けて見ることになるので観測可能です。これが正に虹を作る光なのです。しかし、光の旅路はこれで終わりではありません。C点で反射して内部に戻された光は、D点でまた一部が外に出て来ます。この光は上空に向かって行きますから、地上にいる人には関係ないように思えるかもしれません。ですが、初めの太陽光線の入射位置が水滴の下側だったらどうでしょうか。ちょうど図1を上下逆さにした状態になりますから、D点から出た光も、地上の人から見える方向になる可能性がありますね。これが2つ目の虹、「副虹」を作る光なのです(これに対してC点からの光でできる虹を「主虹」と呼びます)。D点でも一部の光は反射されて内部に戻り、これ以降も延々と反射を繰り返して水滴の内部をグルグル回ります。そして水滴の壁にぶつかるたびに一部の光が外に出て来るのですが、この過程を繰り返すごとに光は弱くなって行きますから、3つ目の虹が見えることはほとんどありません。というわけで、虹について見て行くには、図のC点で出て来る光とD点で出て来る光を考えればよい、ということになります。
図1のように光の入射位置と方向を決めてしまえば、その後の経路は自動的に決まります。しかし実際の太陽光線は水滴のあらゆる場所に入射しますから、当然、出て来る光の方向も様々になります。これでは特定の方向に虹ができることが説明できません。そこで、入射の条件を細かく変化させて、その後の光の経路がどのようになるかをさらに詳しく調べてみます。水滴の屈折率を1.333(黄色の光に対する屈折率に相当)として、水滴のいろいろな場所から入った光の経路を計算した結果が図2で、(a)は主虹を作る光、(b)は副虹を作る光です。図2(a)では水滴の上半分だけに光を入れていますが、下半分に入る場合は上下がひっくり返る形になります。この場合、出て来た光は上空に向かって行きますから、地上にいる人からは見えませんので省略しています。同じ理由で図2(b)では逆に下半分に入る光だけを示しています。
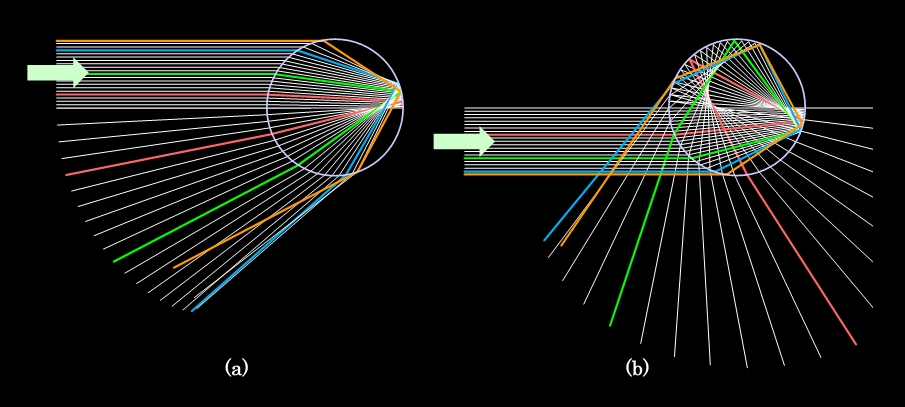
図2 水滴中の光の経路を詳しく見る
どの光がどこに出て来るのかがわかりにくいので、何本かの光の経路に別の色を付けてみました(もちろん、これらは実際の光の色とは関係ありません)。まず図2(a)の方ですが、入射位置が水滴の中心に近い場合と比べて、水滴の端の方に近づくにつれて(赤線→緑線→青線の順に)、より下向きの方向に、つまり入射光線に対して大きな角度で出射することがわかります。ところが、青線よりもさらに中心から外れた位置、ほとんど水滴の端スレスレに入った光(橙線)は、一転して角度の小さい方に戻って来ます。実はこの方向の反転が、非常に重要なポイントなのです。
図2(b)の副虹の光の場合は、角度変化の方向が逆になります。水滴の中心近くに入った光は入射方向に対して鈍角、つまり真下よりも右の方向に行ってしまいますが(赤線)、入射位置が水滴の端に近づくにしたがって緑線のように角度が小さくなり、青線の位置で最小角度になるのです。さらに入射位置が端の方になると(橙線)、図2(a)と同様に角度変化の方向が反転して、また少し角度が大きくなる方向に戻って行きます。
この角度変化の様子をグラフにすると、図3のようになります。横軸は入射位置を示しており、左端が水滴の中央、右端が水滴の端スレスレの位置です。縦軸は入射光線と出射光線の角度で、図3(a)が主虹の場合、図3(b)が副虹の場合です。このような図にすると、先ほど説明した角度の変化がよくわかると思います。主虹の光には極大値が、副虹の光には極小値が現れるのです。
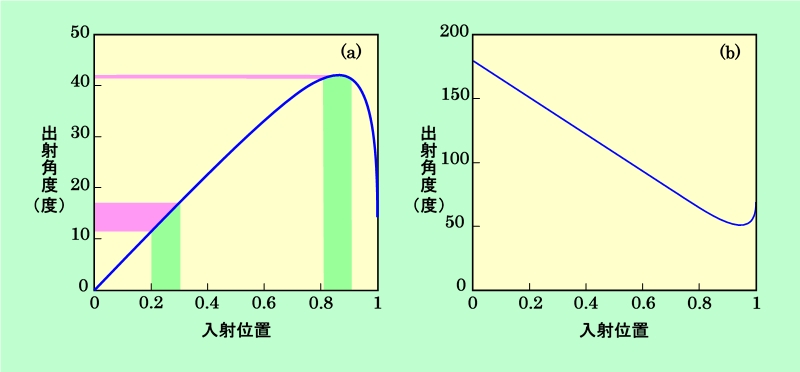
図3 水滴から出て来る光の角度変化
ところで、図2をよく見てみると、入射光線は等間隔に並んでいるのに(そうなる条件で計算したので当然ですが)、出射光線は線の混み具合に差があるのがわかります。どうやら、ちょうど折り返し点付近(青線のあたり)で最も密になっているようです。このことは図3でも確かめることができます。図3(a)には薄緑色の帯が2つ描かれています。一つは左の方、もう一つは極大値付近です。2つの帯の幅は同じですから、この範囲で入射する光の量は同じです。ところが、これに対応する出射光線の方は、図に薄紫の帯で示しているように、両者で幅がずいぶん違いますね。つまり、極大値付近では出射光線が狭い角度範囲にギュッと圧縮されるのです。
この様子をもっとストレートに表現したのが図4です。横軸は出射光線の角度で、図3の縦軸と同じですが、主虹の光と副虹の光の両方を一つのグラフにまとめています(副虹の光のうち鈍角で出て行く部分は、どっちみち見ることができないので省略)。縦軸はその方向に出て行く光の強度で、先ほどの出射光線の密度に相当します。ただし、単純に図2の光線の数密度で計算しましたので、光そのものが反射などで弱くなることは考慮されていませんから、実際の光の強度とは少し違います。
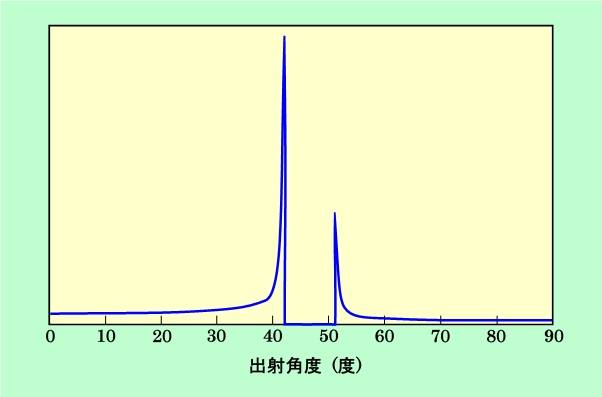
図4 出射方向によって光の強度は変わる
図2では光線の数をかなり間引いていますので、折り返し点付近の光の集中があまり目立ちませんでしたが、もっと細かく計算すると、図4のように主虹と副虹に対応する特定の角度で強度が突出することがわかります。もっともプリズムの場合には光は完全に特定の角度に集中し、その他の方向はゼロですから、それと比べれば集中度は低いですが、それでもかなりのレベルで一方向に偏っていると言えます。これが、球形の水滴でも特定の方向への散乱光が強くなる理由で、決まった角度に虹が現れる原因になっているのです。(ちなみに、図1のB点で出て行く光については、このような特定の方向が強くなる特徴は見られません)
ついでですが、図4でもう一つ目を引くのは、主虹と副虹の間の角度で、光の強度が完全にゼロになることです。図2でもわかりますが、折り返し点の外側には光が全く届かないのです。このことは、後で出て来るように、実際の虹の見え方にも影響します。
水滴が作る虹
以上の説明で、球形の水滴による散乱でも、プリズムのようにに特定の角度に強い光が出て来ることがわかりました。次は光の波長、つまり色による方向の違いです。一般的に物質の屈折率は、光の波長が短いほどが大きくなり、波長の短い紫や青の光の方が波長の長い赤い光よりも、境界で大きく曲がります。水の場合ですと、波長700nmの赤い光に対する屈折率は1.329、波長540nmの緑の光に対しては1.335、波長400nmの紫の光に対しては1.343ぐらいで、赤と紫でも差は1%程度ですが、このくらいの屈折率の差でも、そこそこの角度差が生じます。実際に波長700nm(赤)、540nm(緑)、400nm(紫)の3本の光について光の経路を計算してみると、図5のようになります。(紫の光については、赤との区別がつきにくいので、青色で表示しています)
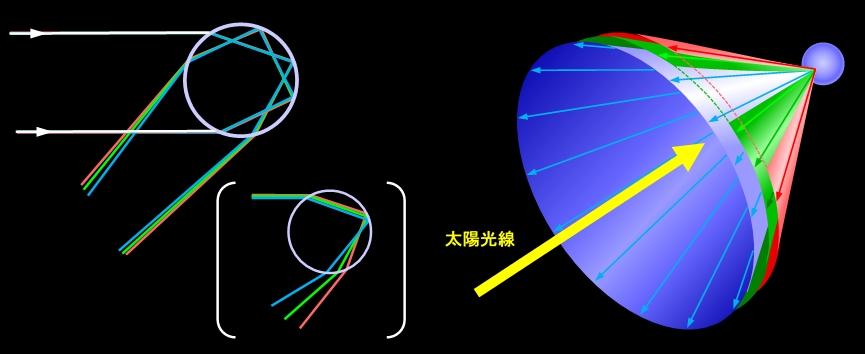
図5 水滴による分光の様子
図5左は3本の光の経路を計算した結果で、主虹の光と副虹の光の両方を示しています。もちろん、水滴の上側に入って下から出て来るのが主虹、下側から入って上から出て来るのが副虹の光です。主虹の出射角度は入射光線に対して、赤が42.7度、緑が41.8度、紫が40.6度で、紫が最も鋭く折れ曲がり、上から紫、緑、赤の順に並んで出て来ます。一方、副虹では、赤が49.7度、緑が51.4度、紫が53.5度になり、主虹と逆に赤が一番上に来ています。赤と紫の角度差は、主虹で2度ぐらい、副虹で4度弱ですから、ガラスのプリズムとだいたい同じレベルでしょうか。この程度の角度差でも、10mも離れれば50cmほどの違いになりますが、それでも正確な図では色による違いがちょっと見にくいので、主虹の光について波長による屈折率の差を10倍に広げた誇張図もカッコ内に示しておきました。虹の説明では、このくらいの誇張した図が使われることが多いので、こっちの方が見慣れているかもしれません。
図5の左の図は平面で描いていますが、実際の水滴からは立体的に光が放たれています。例えば赤の光なら、入射する太陽光線の方向から(主虹の場合)42.7度になる全ての方向に光が出ますので、図5右のように、水滴を頂点、太陽光線の方向を中心線とした円錐の母線に沿ったあらゆる方向に光が放たれることになります(円錐の頂点の角度は色によって違います)。この円錐の側面上のどこかに眼を持って行けば、水滴からの光を見ることができるのです。ただし、無数の光のうち人が実際に見ることができるのは、たまたま眼のところに来た光だけですので、一個の水滴が放つ光のほんの一部分しか眼には入りません。また色の違う円錐は頂点の角度が違い、先ほど書いたように水滴から10mも離れれば光が届く位置が数十cmもズレますから、一個の水滴から出る各色の光の中で実際に見ることができるのは、ほとんど一色のみ、と言ってもよいのです。
このように一個の水滴からはほとんど一色しか見えないのですが、水滴が大量に浮かんでいれば話は変わります。図6に、その様子を示しました。左の図は主虹の場合で、実際の角度では色の差が小さすぎて見にくいので、色による角度差を約8倍に広げて描いています。
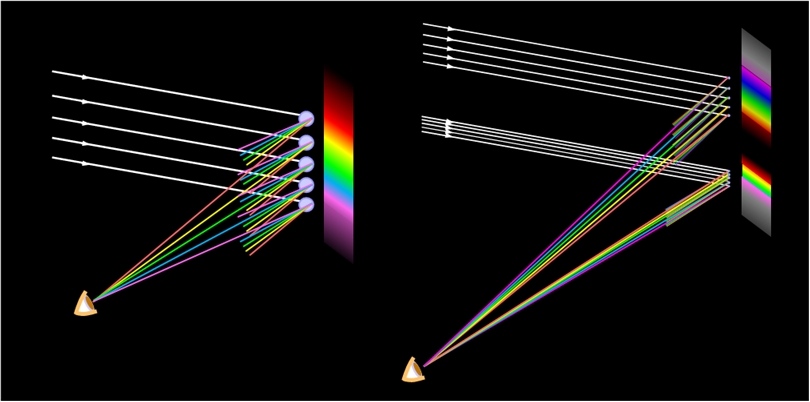
図6 多数の水滴があることで虹が見える
図の一番上の水滴から出る各色のうち、眼に届くのは赤い光だけで、他の色は頭の上を通り過ぎてしまいます。2番目の水滴では、赤い光は下に逸れてしまいますが、代わりに黄色い光がちょうど眼の位置に来ています。同じようにして、違う位置にある水滴から違う色が眼に届くことになり、上が赤で下が紫の虹が見えることになるのです。
これを実際の出射角度で正しく描いたのが図6の右側の図です。主虹を作る水滴群のずっと上の方にある水滴からは、より急角度で降りて来る副虹の光も眼に届いています。副虹の色の順番は主虹と逆になりますので、上が紫で下が赤です。また、図4のところで「主虹と副虹の間の角度には水滴からの光が全く届かない」と書きましたが、このことを反映して、主虹と副虹の間は暗く見えます。これに対して両方の虹の外側には弱いながらも水滴からの散乱光がありますので、内側と比べてやや明るく見えることになります。
ところで、観測者から水滴を見た時に眼と水滴を結ぶ線、例えば、図6の赤い線と太陽光線(白い線)とが作る角度がちょうど42.7度になれば赤の光が見えるわけですが、この条件を満足する方向は一つではありません。眼の位置を頂点として、太陽光線の方向を中心線に、この赤い線をぐるっと一回りさせてできる円錐の側面は、全てこの条件を満たしています。その様子を図7に示します。この図で、太陽光線を示す橙線と水滴からの散乱光を示す赤線との角度は全部同じになっていることがわかると思います。また、図では円錐の底面の縁で散乱する光しか描いていませんが、円錐の側面上ならばどこでも、条件は同じです。つまり、この円錐の側面上にある水滴からの赤い光は全て眼に入るのです。このように、赤い光が円錐の側面に沿って眼に届きますから、観測者からは、遠くの空中に赤い円弧が浮かんでいるように見えることになります。この時、円弧の半径を観測者から見込む角度は、波長700nmの赤い光の場合は42.7度になるのです(円錐の頂角は、この倍の85.4度)。他の色についても同じで、赤い光とは円錐の頂点の角度が違いますから、色ごとに円弧の直径が変わり、各色が同心円状に並んだ円形の虹が見えるのです。
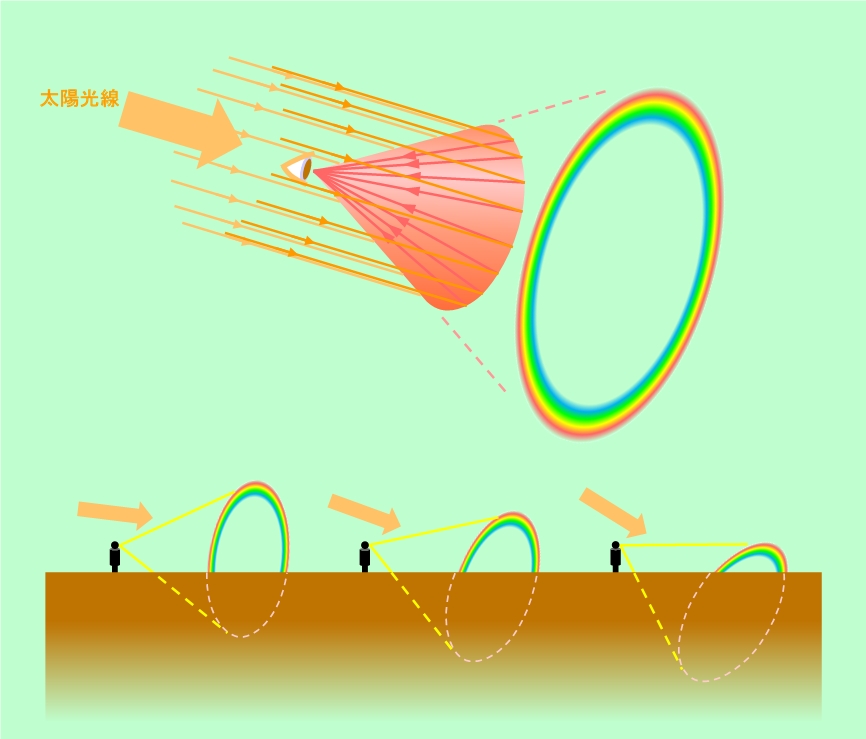
図7 本当の虹の姿は円形
虹が円形になると言っても実際には地面がありますから、普通は全体が見えることはありません。図7の下に示したように、太陽光線の角度が水平に近いときはほぼ半円の大きな虹が見られますが、太陽の高度が高くなるにつれて虹の見える方向も下向きになり、大部分が地面に隠れて(さらに地面の下には水滴もありませんから)、円弧のほんの一部しか見えなくなります。太陽の高度が低い夕方の日没直前に大きな虹が見られるのはこのためです。しかし、例えば飛んでいる飛行機に乗っていて、上に太陽、下に多量の水滴があるような状況では、下方に円形の虹が見えることもあり得るでしょう。
虹の親戚いろいろ
空にアーチ状にかかる虹について一通りの説明をして来ましたが、自然界で見られる虹的な現象はこれだけではありません。そのいくつかを紹介してみましょう。
日暈
日暈は「ひがさ」とか「にちうん」、あるいは単に「かさ」と呼ばれるもので、太陽の周囲に光の輪が現れる現象です。英語では "halo"、つまり「後光」とか「光輪」を表すのと同じ言葉が当てられており、なるほど太陽を取り巻く「後光」のように見えなくもありません。虹は水滴による分光現象でしたが、日暈は太陽と観測者との間に氷の結晶でできた薄い雲(高層にできる巻雲など)がある時に発生します。
氷の結晶の基本形は六角柱です。何となくプリズムに似ていますね。実際に六角柱の氷に光を入れてみると、図8のようにプリズムのような働きをする場合があります。
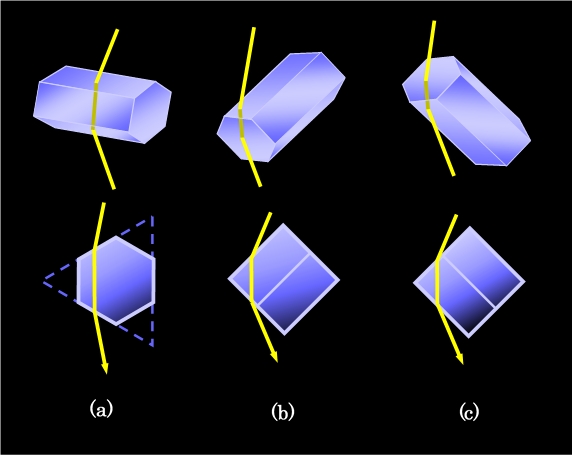
図8 氷の結晶はプリズムになる
図8(a)は六角柱の側面から光が入り、一つ飛ばした別の側面から出て行く場合です。底面側から見た左下の図でわかるように、これは正三角プリズム(60度プリズム)と全く同じ状態です。これに対して図8(b)は、六角柱の側面(四角形の面)から入り、底面(六角形の面)から出て行く場合、図8(c)は逆に、底面から入り側面から出て行く場合で、これらは頂点が90度のプリズムに相当します。この他に、側面から入って隣の側面に向かうパターンも考えられますが、この場合は出て行くところで全反射になってしまうので、光が外に出て来ません。また側面から入って反対側の側面から出る場合は、入った光が同じ方向に出て行きますので、日暈の現象とは関係ありません。
図8では氷の結晶の向きは一つしか示していませんが、実際に空気中に浮かんでいる氷の粒はバラバラな方向を向いています。例えば図8(a)の下側の図のように六角形の頂点がキチンと真上と真下に来るとは限らないわけです。そこで、氷の結晶の向きをいろいろと変えて、出て行く光の方向がどのように変化するかを調べてみると、図9のようになります。左側が図8(a)の結晶を回転させた場合、右側が図8(b)や(c)の結晶を回転させた場合です。
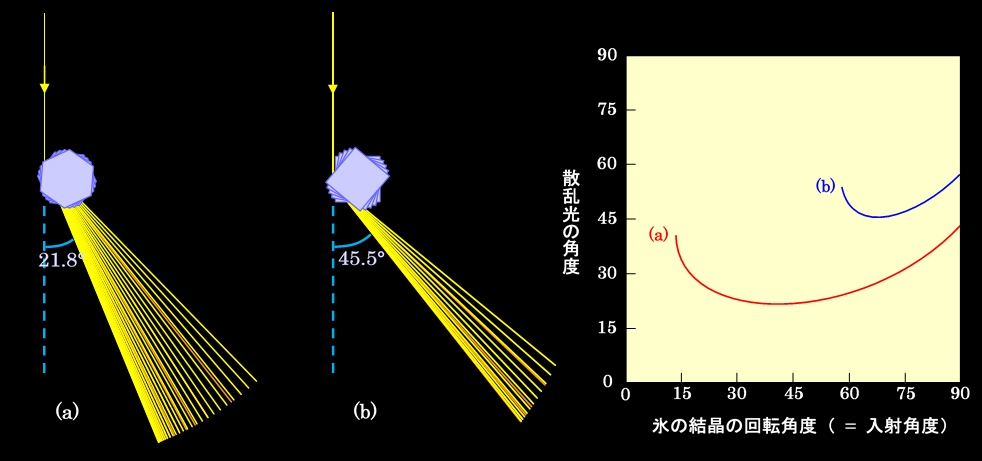
図9 氷の結晶による散乱は水滴と似ている
どこかで見たような図ですね。そうです。水滴による散乱を示した図2とよく似ているのです。図の右側には、結晶の回転角(光が面に垂直に入射する時を0度としていますので、これは面に対する光の入射角度でもあります)によって出射方向がどのように変化するかをグラフにしたものを載せていますが、これも水滴の場合の図3と似ています。角度が小さいところでグラフの線が途切れているのは、全反射を起こして光が外に出て来なくなるからですが、光がちゃんと出て来る条件では、(a), (b)どちらの場合も出射角度が極小値を持つのです。
ここで虹の時と同じように光線の密度に注目してみると、出射角度が最小になる辺りで密になっていることがわかりますね。このように氷の結晶から出る光も、全ての方向に均一に出るのではなく、特定の方向に偏るのです。その角度は、氷の屈折率を1.309とすると、図9(a)が21.8度、図9(b)が45.5度になっています。もちろん光の波長によって屈折率は変わりますので、色が違えば、光が強く出て行く方向も少し変わりますが、およそ22度と46度の方向になると言えます。(この話は、
虹の話(その1)の図3のところで説明した最小偏角そのものです。ガラスの正三角プリズムでは最小偏角は40度付近でしたが、氷はガラスよりも屈折率が小さいので22度まで下がって来るのです)
ただし、氷の結晶と水滴とでは大きく違う点があります。それは、球対称の水滴では一個の水滴から全ての方向の光が同時に出るのに対して、方向性のある氷の結晶では、その向きに応じた一方向の光しか出ない、という点です。水滴の場合は図2のたくさんの光が同時に出ますし、それだけではなく、水平方向を回転軸にして図2を縦に360度回した全ての方向に光が出ます(同じ角度の光は図5のような円錐を作ります)。これに対して氷の結晶では図9の中のどれか一本だけ、しかも水平方向についても、(図では右方向に出ていますが)左かもしれないし右奥かもしれないし、とにかく一方向だけに限定されるのです。とは言っても、雲の中には無数の氷があり、それぞれバラバラな方向を向いているのですから、全体を平均すれば、可能性のあるあらゆる方向の光が同時に出ていることに変わりはありません。一個一個が全方向を担当するか、個々は別々の方向を担当しながら全体として全ての方向を網羅するかの違いであって、観測する側から見れば同じように見えることになります。結果的に、図9で示した方向全てに光が出て、その中で入射光線に対して22度と46度という特定の角度に強い散乱が見られる、という状況になるわけです。(この状況は、
結晶の話で書いている、粉末によるX線回折や電子線回折とよく似ています)
太陽光線に対して特定の角度に強い散乱光が出るということは、虹と全く同じ状況ですね。と言うことで、日暈の場合も、図10のように観測者を頂点、太陽光線の方向を回転軸とした円錐の側面に沿って光が来るように見え、円環状の日暈ができることになります(左が内暈、右が外暈の場合です)。たくさんある氷の結晶のうちで、たまたま円錐の側面上にあり、角度もピッタリ合った結晶からの光が眼に届くわけで、内暈の場合は、図に示したように六角柱の長手方向を円錐底面の円周方向に向けた結晶が実際に働く結晶です(もちろん、回転角も合っていなければなりません)。外暈の場合は、長手方向を太陽光線の方向に向けた状態から一定角度だけ傾けた配置の結晶が暈を作るのに関与します。図では観測者に向かって放射状に開くように傾けた図8(b)に対応する形のみを示していますが、図8(c)に対応する、観測者に向かって閉じるように倒した形の結晶も、同じように働きます。
図9からわかるように、最も光が強くなる方向よりも小さい角度には光の散乱が全くないのに対して、大きい角度にはそこそこの散乱があります。そのため主虹と副虹の間が暗くなるのと同じように、暈の内側は急に暗くなり、一方、外側は徐々に暗くなります。
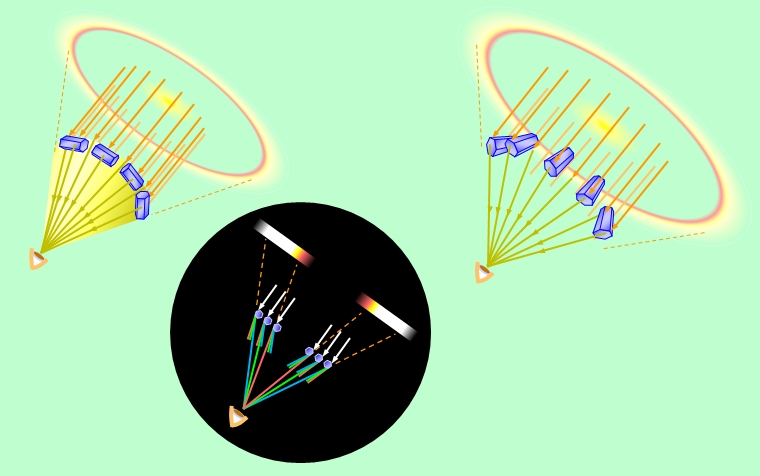
図10 丸い日暈ができる
日暈でも虹と同じように色によって散乱角度が少しずつ違っていますから、色づいて見えることがあります。その場合、屈折率が小さい長波長の光ほど散乱角度が小さいので、図10の黒丸内に模式的に示しているように円錐の頂角が小さくなって内側に見えることになります。つまり日暈では、主虹とは逆に内側が赤で外側が紫です。ただし図9からもわかるように、最も強い散乱光が出る方向よりも大きい角度の側にもそこそこの散乱がありますから、例えば緑や青の光が強く出る方向には赤い光も少し重なり、色が混ざってしまいます。さらに氷の結晶は形も向きも揃っておらず、余分な散乱や反射も多いので、色がきれいに分かれることは少ないようです。それでも、暈の内側は短波長の色が混ざって来ないので、最内の赤や黄色がボンヤリ見えることはあります。
暈の半径を見込む角(円錐の頂角の半分)が22度の暈は内暈(うちがさ、ないうん)あるいは22度ハロ、46度の暈は外暈(そとがさ、がいうん)、46度ハロ、などと呼ばれます。外暈は内暈と比べて光が弱く、見えることは少ないようです。しかし条件によっては六角柱以外の形の氷の結晶によって別の角度の暈が見えることもあるそうです。さらに、太陽だけでなく月によっても暈ができることがあり、「月暈(つきがさ、げつうん)」と呼ばれています。
氷の結晶の中に、六角柱と言うよりも扁平な六角板状のものが多く含まれることがあります。このような結晶は、空気の抵抗を受けて、六角形の面が水平になる傾向があります。内暈を作る結晶の中で、六角形の面が水平になっている部分と言うと、ちょうど太陽の真横(太陽と同じ高度)の位置ですから、扁平な結晶が多いと、この方向からの光が特に強くなることがあります。特に太陽高度が低い場合、太陽の真横に当たる内暈の部分が非常に明るく輝き、まるで別の太陽があるかのように見えるので、「幻日(げんじつ)」と呼ばれます。本当の太陽が、虹色の幻の太陽を両脇に抱えているような感じです。なお、幻日は太陽高度がある程度高くても現れますが、その場合は水平になった氷のプリズムに対して太陽光が斜め上から入るので、屈折光が強く出る方向が22度よりも大きくなり、内暈の外側に幻日が見えるようになります。
環天頂アーク
太陽高度が低い時に、空高く、天頂近くに現れる虹が「環天頂アーク」です。普通の虹と違って太陽の方向の高い空に、太陽側に凸になった弧を描くので、「逆さ虹」などとも呼ばれます。英語では "circum zenithal arc"。つまり、「環状に取り巻く(circum)」「天頂あたりの(zenithal)」「円弧(arc)」という意味になります。日暈と同様に、雲の中の氷の結晶による光の屈折で起こる現象ですが、日暈と違うのは、氷の結晶が六角柱と言うよりも六角板という感じの平べったい形の時に現れることです。幻日のところでも書いたように、このような平べったい形の結晶は、空気の抵抗を受けて水平になって漂うことが多いので、六角形の面が太陽光線に対して常に一定の角度を保つことになります。
環天頂アークを作る光の経路を、図11に示します。太陽光線は六角形の面に斜めに入り、狭い側面から出て行きます。もうお分かりと思いますが、これは図8(c)の外暈と同じ形で、頂角が90度のプリズムとして働いているのです。日暈の場合は氷の結晶の向きがバラバラでしたから屈折光の方向も様々で、そのうち最も光が集中する方向に強い散乱が起こりました。しかし環天頂アークの場合は氷の結晶の向きは固定されていますから、太陽光線の方向が決まれば屈折光の方向も決まってしまいます。この時、氷の屈折率が光の波長によって違うので、左下の図のように色ごとに方向が分かれて虹が見えるのです(図では太陽高度が30度の時の、波長700nm(赤)、540nm(緑)、400nm(紫)の光の経路を示しています)。
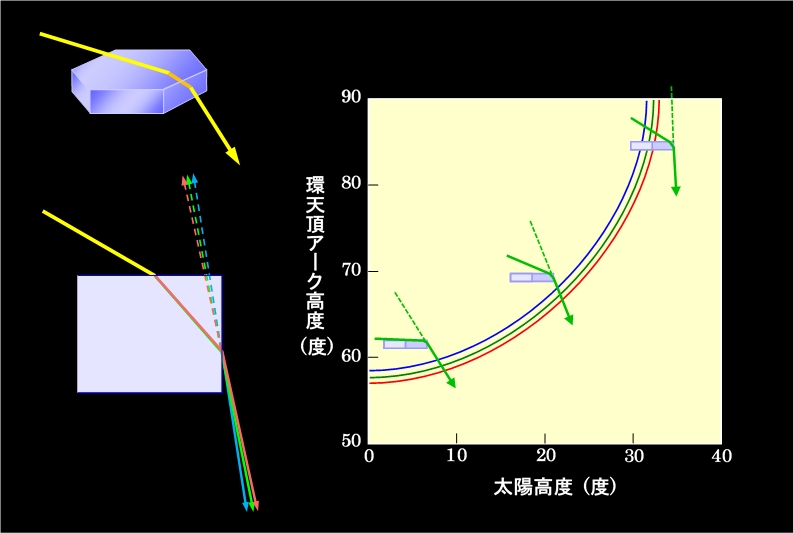
図11 環天頂アークも氷のプリズムでできる
図11右のグラフは、太陽高度と環天頂アークが現れる高度の関係を、3つの波長の光について示しています。太陽高度が0度(入射角で言えば90度)、つまり日の出直後や日没直前の時間帯では、環天頂アークは上空58度付近に現れます。太陽高度が上がって行くと環天頂アークの高度も高くなり、太陽高度32度(入射角58度)付近でついに真上に来ます。真上から光が来るということは、氷の結晶を出た光が垂直の側面ギリギリを降りて来ることを意味しますから、この角度が限界で、これよりも太陽高度が高くなると、結晶に入った光が側面で全反射して外に出られなくなります。つまり、32度以上の太陽高度では、環天頂アークは見られなくなるのです。
以上の説明は、全て真横から見た時の話でしたが、これだけでは環天頂アークが円弧を描く理由がわかりません。それを理解するには、図12のような真上から見た様子を考える必要があります。
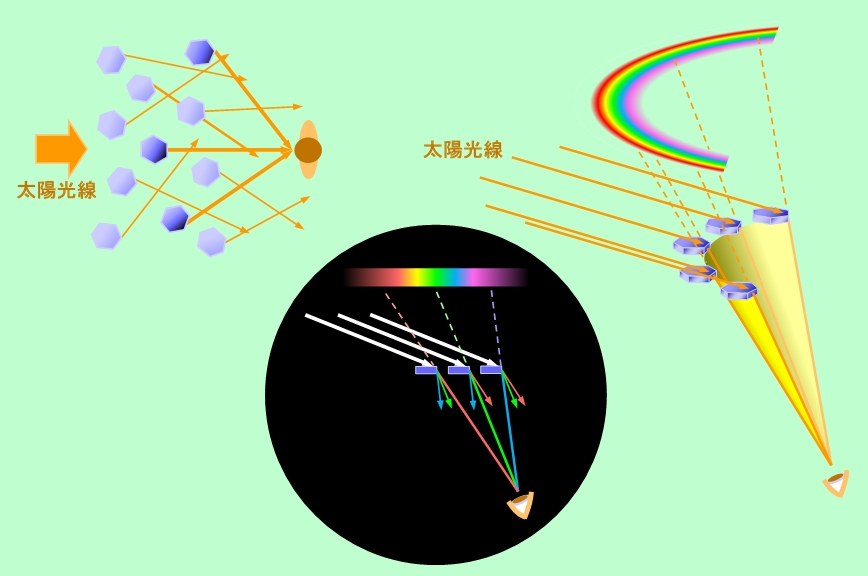
図12 環天頂アークが円弧に見えるのは?
図12左のように、真上から見ると氷の結晶の六角形が見えますが、その向きは当然ながらバラバラです。太陽光線の方向は左から右ですが、光の出口に当たる六角板の側面は、光の入射方向に対して直角とは限らず、様々な向きに傾いているのです。そのため、出て行く光が横方向に曲げられて、結晶ごとに違う方向に進むことになります。地面に対しては同じ角度なのですが、横方向は結晶ごとにバラバラ、ということです。このような状態になると、ほとんどの光は観測者の眼から逸れてしまいますが、たくさんの結晶の中にはちょうどよい向きのものも含まれているはずですので、一部の光はちゃんと観測者に届きます(図12左の例では、濃い色で示した結晶からの光は観測者に向いています)。このように、地面との角度が一定という条件で観測者に届く光を集めると、図12右のように、観測者の眼を頂点、天頂方向を中心線とした円錐の一部が形作られます。この円錐の側面に沿って光が届くことで、太陽に向かって凸の円弧ができるのです。
図12の黒丸の中に、横から見た断面の様子も示しておきました(色による角度差は実際よりも誇張しています)。この図の向きで言うと、左の方(太陽に近い方)の結晶からは小さい角度で屈折した赤い光が、右の方(太陽から遠い方)の結晶からは大きい角度で屈折した青や紫の光が眼に届き、太陽側が赤、反対側が紫の虹ができることがわかります。上下がひっくり返った「逆さ虹」ですが、アーチの外側が赤で内側が紫ですので、主虹と同じ配色とも言えるでしょう。
環天頂アークは太陽の高度によって様々な方向に出るのですが、その明るさは高度によって違います。その原因は、氷の結晶が完全に水平に揃っているわけではなく、角度が多少はバラつくことにあります。ここで再び図9のグラフを見てみましょう(直角プリズムなので(b)の方)。結晶の角度が少し変わると屈折光の出射角度も変わるのですが、その変化の仕方が、極小値付近では小さく、そこから離れるほど大きくなることがわかります(横軸方向に同じ幅だけズレた時の縦軸方向の変化幅を見てください)。つまり、出射角度の極小値付近では、結晶が多少バタついても、光の方向が大きくは変化しないのです。そのため光が広がってボヤけることが少なく、シャープな虹が見えることになります。ですから図9の極小値の条件に当たる太陽高度22度(氷の面への入射角度68度)の時に、68度の高度に現れる環天頂アークが最も鮮明、ということになるのです。
この時の入射太陽光線と出射光線の角度は46度ですから、外暈と全く同じです(同じ原理ですから当然です)。ということは、太陽高度が22度の時に外暈が現れると、同じ位置に明るい環天頂アークが重なることになります。円弧の向きが逆ですから、外暈の円に環天頂アークの円弧が接する形の面白い光景が見られるかもしれません。
環水平アーク
環天頂アークと双子のような関係にある現象が「環水平アーク」です。環水平アークは環天頂アークとは逆に、太陽高度が高い時に、太陽の下の方に水平に伸びる虹で、英語では "circum horizontal arc"、つまり、「環状に取り巻く(circum)」「水平な(horizontal)」「円弧(arc)」です。環水平アークを作るのは、環天頂アークと同じ六角板状の氷の結晶ですが、図13のように、光の出入りが逆になっていて、太陽光は六角板の側面から入って底面から出て来ます。言うまでもありませんが、これは図8(b)と同じ形です。
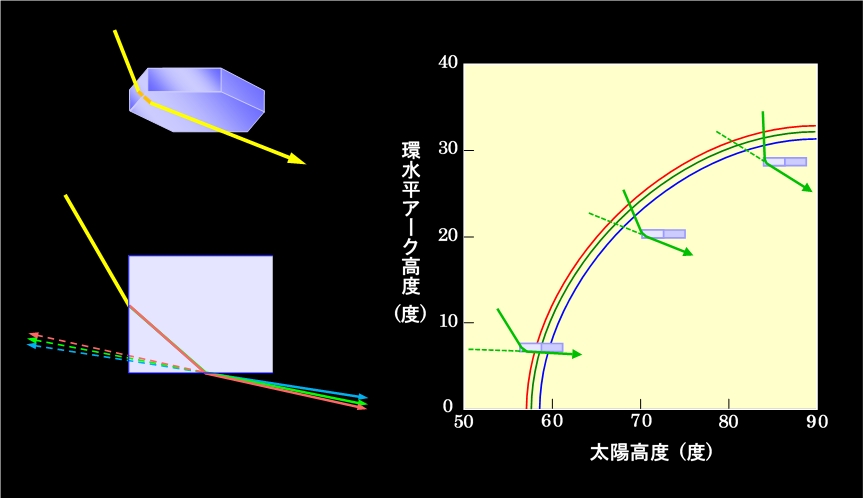
図13 環水平アークも氷のプリズムが原因
図の右側は、太陽高度と環水平アークが現れる高度の関係を示すグラフです。環天頂アークとは逆に、太陽高度が58度以下では、氷の結晶の中に入った光が内部で全反射して出て来ませんので、環水平アークは現れません。日本での太陽の南中高度は、春分や秋分の時期で55度ぐらい、冬至の頃では32度ぐらいですから、日本で環水平アークが見られるのは夏場だけ、ということになります。太陽高度が58度を超えて来ると、六角板の底面スレスレに、つまりほぼ水平に屈折光が出て来ますから、低い位置に環水平アークが見えるようになります。太陽高度が上がるにつれて環水平アークも上昇し、太陽が真上に来ると、32度の高度に見えるようになるのです。なお、環水平アークの場合も環天頂アークと同様に、太陽光と屈折光の角度が46度になる時に最も明るくなります。その時の太陽高度は68度で、環水平アークの高度は22度です。
環水平アークも、環天頂アークと同じ理屈で円弧状になります。その様子を図14に示しました。
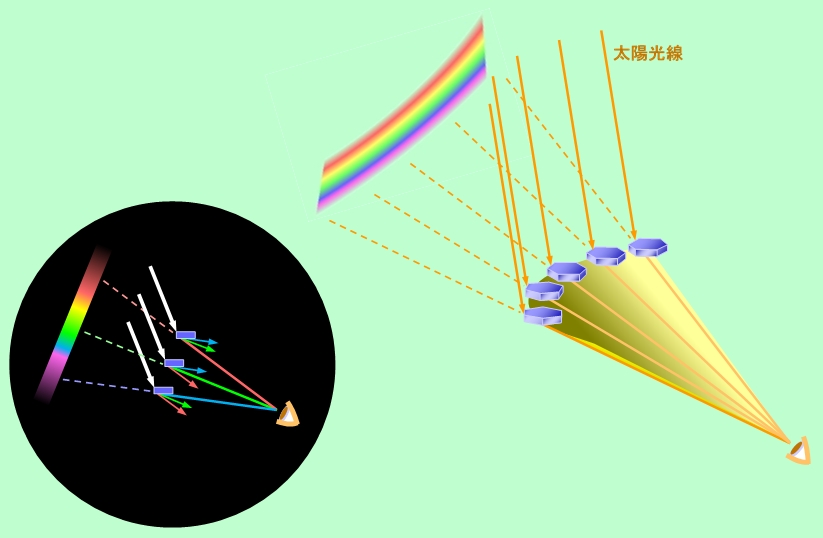
図14 環水平アークも実は円弧状
あれっ、「水平」なのに「円弧状」? と思われるかもしれませんが、地平線や水平線だって、自分の周りをぐるっと取り囲む円ですよね。環水平アークも実際の形は円弧なのですが、円の半径が大きいので、現れる位置が低いと地平線とほぼ平行になり、ほとんど水平に見えるのです。それでも高度が上がって来ると、環水平アークも下に凸の少し反った形に見えるようになります。
黒丸内の図に示すように、太陽に近い側にある結晶からは屈折角度の小さい赤い光が、太陽から遠い側にある結晶からは屈折角度の大きい青や紫の光が眼に届きますから、環水平アークでも環天頂アークと同じように太陽側が赤、反対側が紫の虹になります。少し下に凸に反ることを考えると、アーチの内側が赤で外側が紫ですから、主虹とは逆の配置になっているとも言えますね。
タンジェントアークとラテラルアーク
バラバラな方向を向いた六角柱状の氷の結晶が暈を作るわけですが、この六角柱状の結晶が空気抵抗を受けて水平に(つまり六角形の面が垂直に)なることがあります。このような水平の六角柱結晶だけでは暈はできませんが、結晶の位置と角度がうまく合えば、暈よりも少し外側にある結晶を通って来た光が眼に届くようになります。同じ形の結晶でも、太陽光線の進入角度が結晶の面に対して斜めになると、その斜め方向の断面では頂点の角度が大きくなるため、より屈折角度の大きい方向に強い光が出て、暈よりも大きい角度からの光が見えるようになるからです。このような眼に届く光をつなぎ合わせると一定の形を描き、タンジェントアークやラテラルアークと呼ばれる虹が現れます。
水平な結晶が内暈と同じように60度プリズムとして働いて、内暈の外側に接する形で現れるのがタンジェントアーク(タンジェント(tangent)は「接する」という意味)です。他の現象のように単純な円を描くわけではないので、タンジェントアークの形を感覚的に理解するのは難しいですが、氷の結晶の向きに着目すると、内暈との位置関係が見えて来ます。
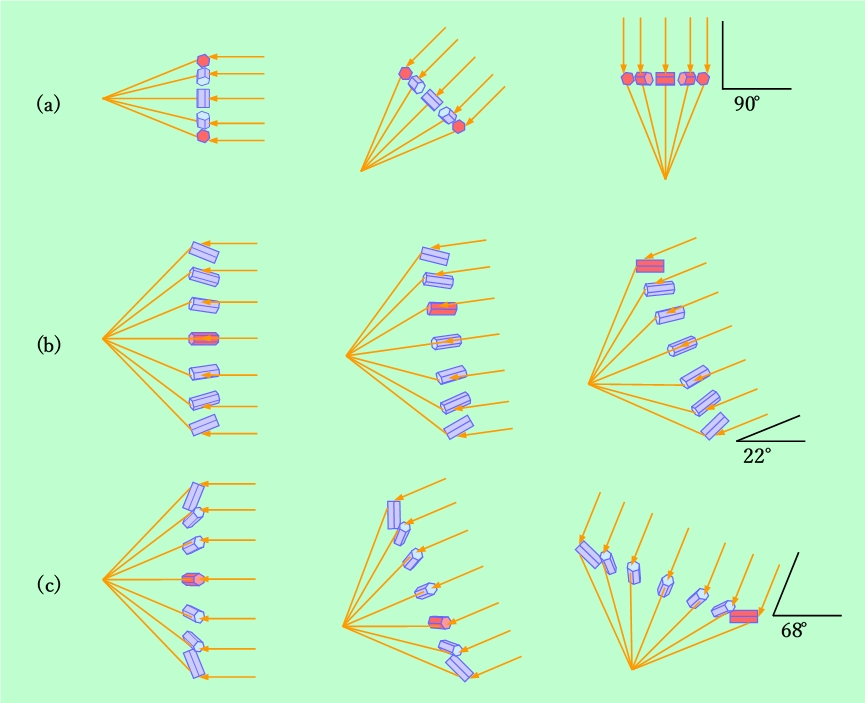
図15 暈を作る結晶の角度が重要
図15(a)は、内暈を作る氷の結晶を真横から見たもので、左端は太陽高度が0度の場合です。氷の結晶は、長手方向が内暈の円周方向に沿うように並んでいますので、暈の真上と真下の位置にある結晶は水平になっています(図では赤で表示しています)。タンジェントアークを作る結晶も水平ですから、このような真上と真下の位置では、同じ結晶が両者に共通となり、タンジェントアークは必ず内暈の真上と真下に接する形になります。真上と真下以外では結晶の向きが違いますので、内暈を作る結晶とタンジェントアークを作る結晶の位置がズレて来て、タンジェントアークは内暈から外に離れます。その結果、タンジェントアークは内暈の真上と真下の部分から左右に髭を伸ばしたような形になるのです。その様子を、他の現象も含めて、図16にまとめてみました。図16(a)が太陽高度が0度の場合で、タンジェントアークは内暈の頂点から「V」字型に斜め上に伸びる形になっています(地平線の下で見えませんが、下側にも逆V字形のタンジェントアークが隠れています)。
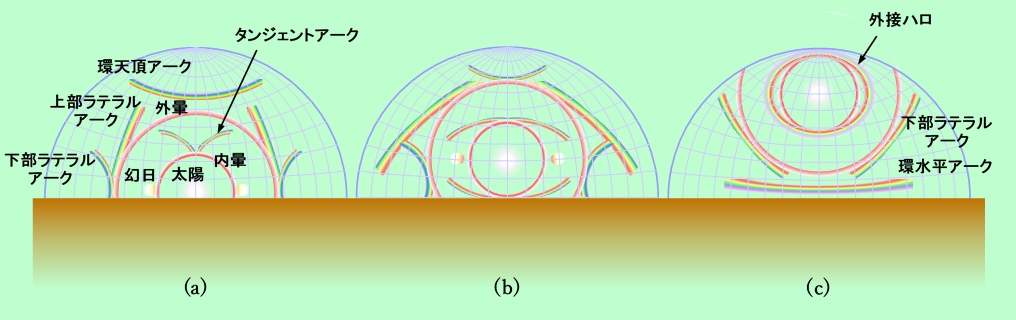
図16 氷の結晶が見せる様々な虹的現象
この状況は太陽高度が高くなっても変わりませんが、図15(a)の中央に示すように、内暈を作る結晶全体が次第に水平に近付いて行きますので、図16(b)(太陽高度は20度付近)のように、タンジェントアークと内暈も接近して行きます。太陽高度が30度を超えて来ると上下のタンジェントアークがつながって、図16(c)(太陽高度は60度付近)のように内暈に上下で接する楕円になります。これを「外接ハロ」と呼びます。太陽高度がさらに上がると外接ハロは円に近づいて行き、太陽高度が90度、つまり太陽が天頂に来ると、図15(a)の右端の図のように内暈を作る全ての結晶が水平になり、内暈とタンジェントアークは完全に一致します。
氷の結晶が外暈と同じように90度プリズムとして働いて、外暈の外側(主に左右)にできるのがラテラルアーク(ラテラル(lateral)は「横の」という意味)です。外暈を作る氷の結晶の向きには、図8(b)と(c)の2つのパターンがありますが、外暈に関しては区別は必要ありませんでした。しかしラテラルアークの場合は、結晶が水平に固定されているので、この両者で太陽光線に対する位置関係が違い、見え方の違う2種類のラテラルアークが現れます。ラテラルアークも単純な形ではないので簡単に説明するのは難しいですが、タンジェントアークと同じように外暈を作る結晶の向きに注目して、外暈との位置関係を見てみましょう。
光が六角柱の側面から入って底面から出て行く図8(b)のパターンで作られるラテラルアークを「上部ラテラルアーク」と呼びます。図15(b)が、これに対応する外暈の結晶の配置で、氷の結晶は観測者に対して放射状に開くように傾いています(傾きの角度は太陽光線に対して22度)。太陽高度が0度の時は、図15(b)の左端の図からわかるように、赤で表示した外暈のちょうど真横の位置で結晶が水平になっています。ですから上部ラテラルアークはこの真横の位置で外暈に接し、真横からズレるに従って、図16(a)のように外暈から離れて上下に伸びる形になります(下半分は地平線の下なので見えていませんが)。
図15(b)中央の図のように太陽高度が少し高くなると、今度は少し高い位置にある結晶が水平になります(やはり赤で表示)。その結果、外暈と上部ラテラルアークの接点もこの位置まで上がり、上部ラテラルアーク全体も上がって行きます。太陽高度がさらに上がって22度になると、外暈の一番上の結晶が水平になりますので、左右の上部ラテラルアークが外暈の真上の位置でつながって、一つの大きなアーチを描くようになります(実際にはもう少し低い太陽高度でも、外暈と重なって、つながっているように見えるようです)。これに近い状態を表しているのが図16(b)です。その後は、外暈を作る結晶に水平なものは存在しなくなるので、上部ラテラルアークは外暈から離れて上がって行きますが、太陽高度が32度を超えると、六角柱状結晶の側面から入った光が六角形の底面で全反射されるようになりますから、上部ラテラルアークは見られなくなります(図16(c))。
次に図8(c)のように、光が六角柱の底面から入って側面から出て行くパターンについて見てみましょう。このパターンで作られるのが「下部ラテラルアーク」です。この場合、対応する外暈を作る結晶の向きは先ほどとは逆で、図15(c)のように太陽に向かって大きく開く配置を取ります(傾き角度は太陽光線に対して68度)。太陽高度が0度(図15(c)左)の場合は、やはり外暈の真横の位置に対応する結晶が水平ですので、下部ラテラルアークも上部ラテラルアークと同じように、真横の位置で外暈に接します(図16(a))。この段階では「上部」、「下部」という区別はピンと来ませんが、ここから先が違います。外暈を作る結晶の傾きが逆なので、太陽高度が高くなると、図15(c)中央のように、赤で示した低い位置にある結晶が水平に向くようになります。つまり、下部ラテラルアークと外暈との接点は、太陽高度の上昇に伴って下がって行くのです(図16(b)〜(c))。さらに太陽高度が上がって68度になると、図15(c)右のように外暈の一番下の結晶が水平になりますから、この時点で左右のアークがつながり、外暈の底で接する形になります。その後は外暈から離れて行きますが、上部ラテラルアークのように消失することはありません。太陽光線は垂直になった六角形の面に沿うような方向から入って来ますから、高度が上がっても結晶面に対する角度がそれほど大きくならず、全反射の条件を満たさないからです。
以上、氷の結晶が作り出す虹的な現象をいくつか紹介して来ましたが、ここに挙げた以外にも、氷の結晶が絡む様々な光学現象が知られています。しかし、話が既に相当長くなっていますので、本稿ではこのあたりに止めて、最後に光の回折による現象を見ておきましょう。
光環
暈と同じように太陽や月の周りに光の輪ができる現象に「光環(光冠)」があります。英語名は "corona"で、王冠(crown)の語源になった言葉ですから、「光冠」の方が英語の意味に近いですが、本稿では「光環」で統一することにします。太陽の周りにできるのが日光環、月の周りにできるのが月光環で、どちらもよく見られる現象です。光環は一見すると暈と似ていますが、暈は、高層の雲を作る氷の結晶による光の屈折、光環は、もう少し低い位置にある雲の水滴による光の回折が原因で起こる現象ですので、原理からして全く別のものです。
光の進路に細かい粒子があると、図17の上段に示したように、その粒子の後ろ側にも光が回り込む「回折」が起こり、さらにこの回折光が互いに強め合ったり弱め合ったりする「干渉」が起こります。その様子を図17下段に模式的に示しました。図17(a)は粒子の直径が光の波長の10倍ある場合、(b)は5倍、(c)は2.5倍の場合です。それぞれ左側が横から見た断面図、右側が、回折光をスクリーンに投影した場合の強弱のパターンを示しています。雰囲気は
回折格子に似ていますが、回折格子では規則的に並んだ突起や溝の部分からの光だけを考えればよかったのに対して、粒子による回折では連続的なあらゆる部分からの光が絡むので、正確に求めるにはずっと複雑な計算が必要です。現象としては、孔(ピンホール)やレンズによる回折現象と全く同じで、
カメラや望遠鏡の解像度に関係して詳細に解析されていますが、ここでは大まかな結果だけを見て行くことにします。
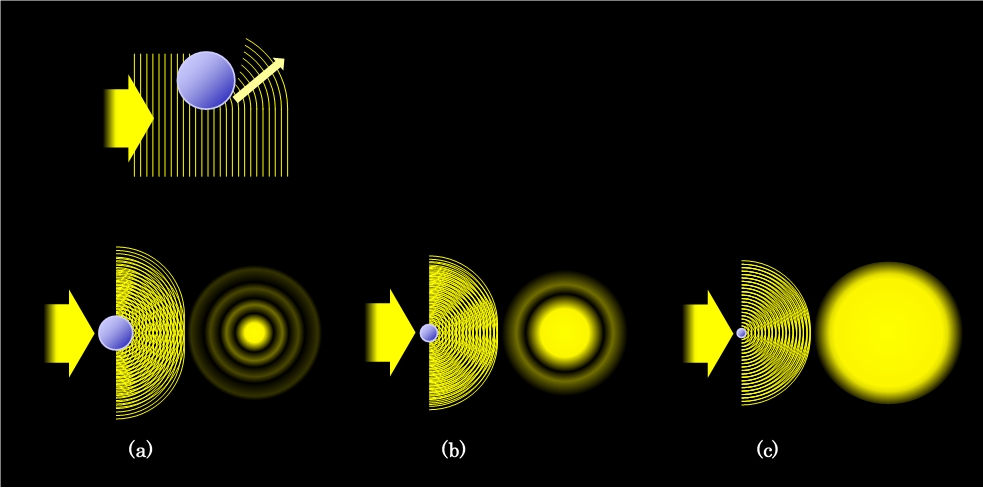
図17 微粒子による光の回折
粒子の直径が光の波長の10倍ある場合、図17(a)のように、中心に円板状の明るい部分(エアリーディスク)ができ、その周りを同心円状に暗い光の輪が取り巻く形になります。この形は粒子径が変わっても基本的には同じなのですが、(b)や(c)のように粒子径が小さくなると、エアリーディスクも周囲の輪も、外へ外へと広がって行きます。現実的には周辺の輪は暗いので無視するとして、エアリーディスクの大きさを、粒子の位置から見込む角度で表すと、(a)が約14度、(b)が約28度、(c)が約58度となります。このように、それまでまっすぐに来ていた光が、粒子のところで、これだけの角度で円錐状に広がる光に変わるのです。たびたび出て来る光の円錐ですが、今回の円錐はちょっと違います。これまでは光線の角度が22度とか46度とかに決まっていたので、光は円錐の側面だけを通って来ました。しかし今回は、決まった角度以下ならば何度でもよいので、円錐の内側全部に光が出るのです。
この現象が太陽や月の手前の雲の中にある水滴で起こる場合を考えましょう。図18のように、平行であった元の光線が、それぞれの水滴のところで円錐状に広がります。
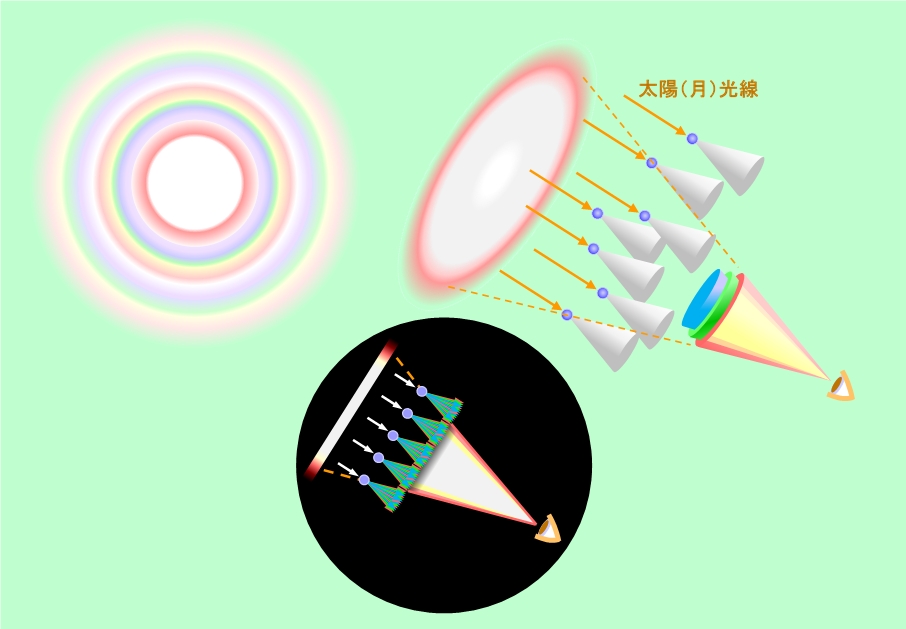
図18 光の回折でできる光環(左上は花粉光環の模式図)
それぞれの水滴から円錐状に出る光のうち、実際に観測者の眼に届くのは、ちょうどよい方向に出て来る一部の光だけです。それらの光を集めると、今度は眼を頂点にして太陽の方向に広がる円錐が描けます。こちらの円錐も、側面だけでなく内側全部が光で埋められますから、これを延長した先に、暈のような輪っかではなく、太陽の周りにボワッと広がった光の円板が見えるのです。水滴から出る円錐と眼のところの円錐は同じ形ですので、水滴での光の広がる角度が、そのまま光環を見込む角度、つまり大きさになります。普通、雲の中の水滴の大きさは数ミクロンから数十ミクロンぐらいなので、光環の大きさは1度〜10度ぐらいと計算できます。太陽の直径が約0.5度ですから、みかけの太陽の大きさの数倍〜十数倍、といったところです。もちろん、水滴の大きさがバラバラですと光の広がり方もバラバラになりますから、きれいな円形の光環にはならず、形が崩れてしまいます。
図17のところで、光の波長に対して粒子の直径が小さいほど、光の広がる角度が大きくなることを説明しました。と言うことは、逆に同じ直径の粒子ならば、波長が長い光ほど大きく広がることになりますので、色の分離が起こってもよさそうです。その場合、波長の長い赤い光が最も大きく広がりますから、暈とは逆に赤が外側で紫が内側に来るでしょう・・・・・と言いたいところですが、光環を作る円錐は、側面だけでなく内部が光で全部埋まっていますから、頂角の小さい内側の円錐には、頂角の大きい外側の円錐の色が完全に被ってしまいます。その結果、内側は全色が混ざって白色、そこから外に向かうに従って紫が抜け、青が抜け、緑が抜け・・・・・と徐々に色が減って、最後に大外の赤が残る、という形になります。結局、単独で見えるのは外側の赤だけで、後は内側が青味で外側が赤味の、全体として白っぽい光の円板になってしまうのです。さらに、光の回折角度は粒子の大きさで変化しますから、水滴の大きさが不揃いだと、やはり色の混合が起こります。このような理由で、白っぽい円の外側に赤い色が滲み出たような光環が見られることはあるものの、色鮮やかなものが見られることは少ないのです。
光環は粒子による回折現象ですから、水滴以外の粒子でも起こります。有名なのが火山灰で、水滴よりも小さいことが多いので、10度以上の大きな光環が現れることもあるようです。また最近よく話題になるのがスギ花粉です。スギ花粉は直径が30ミクロンぐらいで、光の波長の数十倍もありますので、光環の直径は3度ぐらいと小さめです。しかし粒子の大きさが揃っているので非常にシャープで、白い円板の周囲の赤色がかなり鮮明に見えることが多く、さらに図17(a)のような、メインの円板を取り巻く外側の2重、3重の輪がはっきりと現れることもあります。外側の輪は決まった角度にしか出ませんから、この輪を作る光の円錐は側面のみで内部が空洞、つまり他の色が混じらないので、赤から紫までの色がきれいに分かれた円形の虹になります。図18の左上に、この花粉光環を模式的に示した図を載せておきましたが、このように一番内側が白色の円板で、その外周が赤、さらにその外を、内側が紫で外側が赤の虹色のリングが幾重にも取り巻く形になるわけで、なかなか見事なものです。もっとも、花粉症の人にとっては、虹を愛でるどころではないでしょうけど・・・。
彩雲
虹色に色付いた雲のことを「彩雲」と呼びますが、これは見え方が少し違うだけで、基本的には光環と同じ現象です。太陽の手前に幅広く薄雲がかかると光環になりますが、太陽から少しズレた位置にある雲で同じ現象が起こると、円板の全景が見えないので彩雲として見えるのです。また、水滴の大きさが不揃いで、光環の丸い形が大きく崩れたものも、彩雲とされるようです。
光環はあまり色鮮やかにはならないはずでは?、と言いたいところですが、色の付かない光環の一部が雲に現れても、ほとんど雲が日に照らされて光っている程度にしか見えませんので、存在に気が付かないでしょう。要するに、光環の現象が雲に現れた際に、目立った色が付いた場合に限り、彩雲として認識されるわけです。また、雲の中の水滴の大きさは10ミクロンぐらいなので、回折光が広がる半径はせいぜい5度ぐらいです。ということは、彩雲が見られるのは太陽からの距離が5度以内、小さめ(5ミクロン以下)の水滴の場合でも太陽から10度程度、ということになります。これだけ太陽に近いところをじっくり見ることは(目にもよくないですし)あまりないでしょうから、彩雲が出ていても気づかないことが多いのですが、実際には結構な頻度で現れる現象のようです。
鮮やかな彩雲が現れるには、先ほどの花粉光環の話と同じで、水滴の粒径が揃っていることが必要です。また粒径が小さい方が回折角度が大きくなって色の分離が良くなりますし、太陽から離れた位置に出るので見えやすくなります。このような条件を満たすのが、雲の端の方、縁の部分です。雲の縁では周りの水蒸気が少ないので水滴はどんどん蒸発して小さくなっていますし、粒径も比較的揃っていますから、この部分に虹色が見えることが多いのです。また、縁から雲の内側に入るに従って水滴の径が徐々に大きくなる傾向があるため、雲の縁の形を維持したままで内側に向かって色が変わって行ったりもします。さらに、雲の状態は時々刻々変わりますから、彩雲の色や形もそれに応じて様々に変化します。
空全体に薄く広がるような雲の場合は光環になってしまいますが、隙間のある高積雲や巻積雲(ひつじ雲やいわし雲などと呼ばれるヤツです)、あるいは大きな雲から分かれた千切れ雲などが太陽の近くに来た時が、彩雲を見るチャンスです。このような場面に出会ったら、(太陽を直接見ないように何かで隠しながら)注意して観察してみてください。
オマケ ― 簡単な角度の測り方 ―
本稿の全体を通じて角度の話が多く出て来ましたが、実際に空に見える2点間の角度がどのくらいなのかは、(分度器を持ち歩いているわけでもありませんから)感覚的にわかりにくいですよね。そこで最後に、これを大雑把に見積もる方法を紹介しましょう。
角度の"1度"というのは、およそ60cmの距離のところで1cm離れた2点間の角度に相当します。60cmというと、だいたい大人の片腕の長さですから、腕をまっすぐに伸ばした時の手先の大きさ(単位はcm)が、ほぼ見込み角になるのです。個人差はありますが、自分の手の大きさを覚えておけば、指先の幅なら1.5度、握り拳の大きさなら8度ぐらい、手を開いた時の親指の先から小指の先までの幅なら約20度、というぐあいに、簡単に角度を見積もれます。太陽や月の見込み角は0.5度ですから、伸ばした腕の小指の先で余裕で隠れますし、直径5度の光環ならゲンコツの6〜7割、半径22度の内暈ならば開いた掌ぐらいの広がりになるわけです。また虹とは関係ないですが、同じようにして星と星との角度や、流れ星の長さなども測れます。夕日が地平線からゲンコツ1個分の位置にあれば、太陽は1時間に15度動きますので、あと30分ほどで日没になることもすぐにわかるのです。いろいろな場面で使えますから、覚えておいて損はないと思います。
雑科学ホーム
hr-inoueホーム


















